Сущность этого способа заключается в следующем:
1. Линию контура детали по средней линии разбивают на отдельные участки (1.2.), преимущественном на прямые отрезки и части окружности. Криволинейные участки разбивают на отдельные небольшие отрезки, близкие к прямой.
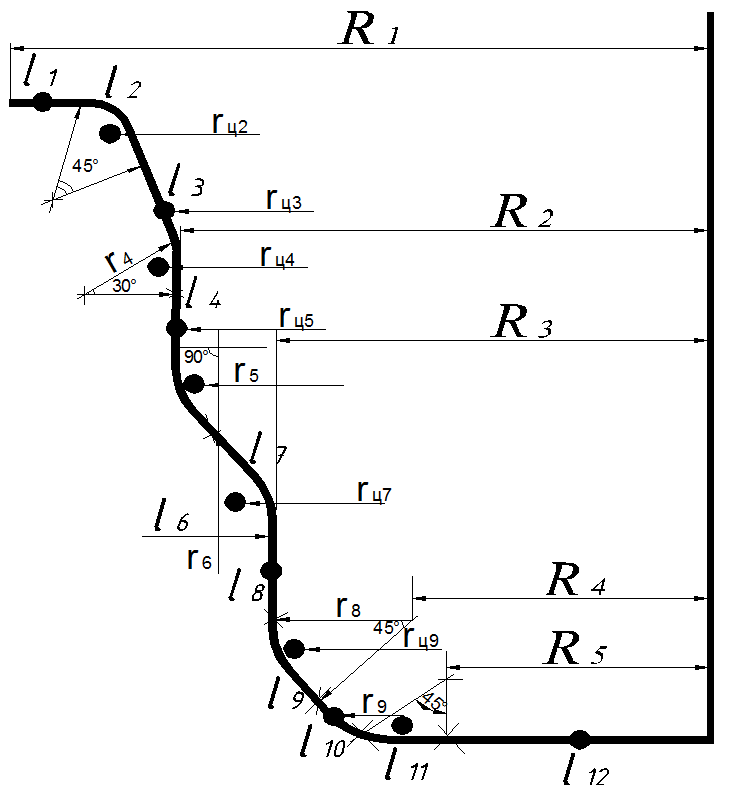
Рис. 1.2. к определению диаметра заготовки графо-аналитическим способом
2. Центр тяжести каждого участка отмечают точкой. Для прямых участков центр тяжести расположен по середине. Для частей окружности положение центра тяжести находится в зависимости от величины центрального угла.
3. Определяют длину участка образующей : для прямых участков- по чертежу, а для дуг- как для части окружности или по табл. 37 и 38 /1/.
4. Перемножают длины участков l и радиусы центров тяжести отрезков r, суммируют и находят
∑ ℓ*r = ℓ * r + ℓ * r +....+ ℓ * r (1.4.)
5. По величине Σℓ*r находят искомый диаметр плоской заготовки согласно формуле (1.3.).
Рассмотренный способ определения диаметра плоской заготовки для вытяжки трудоемок и требует как графических построений, так и значительных расчетных операций. Поэтому, с целью значительного сокращения времени проектирования технологических процессов листовой штамповки, разработана система кодирования чертежа штамповки после формообразующих операций и алгоритм расчета, которые максимально упростят работу по определению диаметра исходной плоской заготовки с помощью ЭВМ.
2. Алгоритм и программа определения диаметра
заготовки
2.1. Кодирование чертежа детали
Для кодирования рассматривают контур детали в плоскости сечения, проходящей через ее ось ( рис. 2.1.а). на половине осевого сечения детали проводят оси Х и У таким образом, чтобы ось Х совпадала с осью детали, а ось У примыкала к донной части ( 2.1.б). система кодирования предусматривает следующие построения ( рис. 2.1.).
Прямолинейные участки контура продолжают до пересечения друг с другом. Точка пересечения (узловым точкам) присваивают номера от 0 до m . Точка i=0 совпадает с началом координат, а с i=m с концом контура.
Для каждой узловой точки определяют координаты по осям Х и У и соответствующие радиусы сопряжения прямолинейных участков контура, используя размеры, указанные на чертеже детали. Если при последовательном обходе контура от i=0 до i=m встречаются радиусы сопряжения r с координатами центра, лежащими с внешней стороны детали, то их значения принимаются со знаком минус. При отсутствии сопряжения по радиусу r - принимают равным 0.
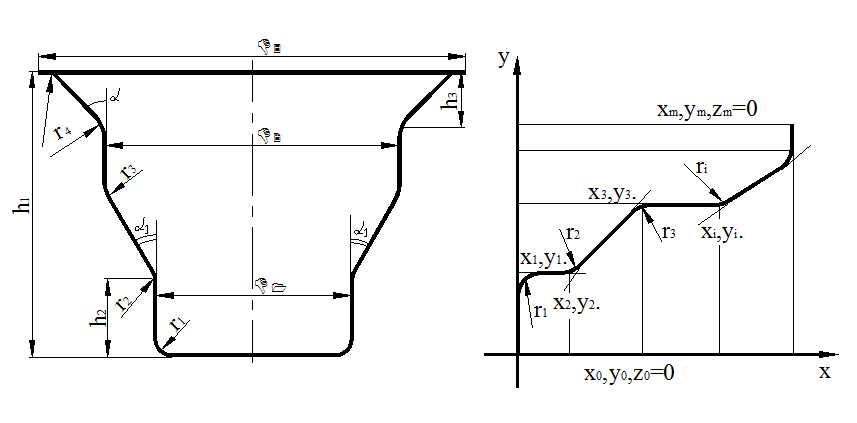Рис. 2.1. Схема координирования чертежа детали
Итак, геометрический образ детали, получаемых вытяжкой, описываются последовательностью чисел х , у , и r , номера которых соответствуют номерам встречи с этими точками при обходе половины контура детали по часовой стрелке.
2.2. Методика аналитического расчета диаметра заготовки
Известно, что определение размеров заготовки для вытяжки производится по равенству площадей поверхности заготовки и готовой детали. Следовательно задача сводится к установлению геометрических соотношений, обеспечивающих расчет площади поверхности детали типа вращения произвольной формы. Площадь поверхности тела вращения, образованного кривой произвольной формы при вращении ее вокруг оси, находящейся в той же плоскости, равна произведению длины образующей на путь ее центра тяжести.
Исходя из разработанной системы координирования чертежа детали, необходимо определить длины прямолинейных участков контура и длины дуг их сопрягающих, а также установить расстояние от оси ”х” до их центров тяжести.
Последовательность расчета включает следующие этапы:
- определение направляющих косинусов прямолинейных участков
контура αi и βi в принятой системе координат;
- определение координат центров радиусов округления контура ;
- определения координат точек сопряжения радиусов округления и прямолинейных участков контура;
- определение длин дуг сопряжения и прямолинейных участков;
- определение центров тяжести дуг и прямолинейных участков;
- определение диаметра заготовки.
На рис. 2.2. предоставлена схема к аналитическому определению направляющих косинусов.
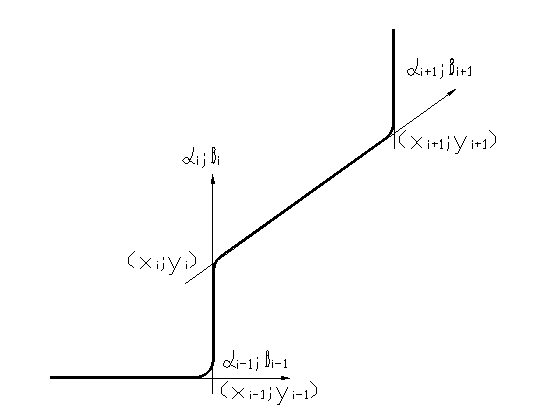
Рис. 2.2. К определению направляющих косинусов
Ниже приведены формулы для определения направляющих косинусов αi и βi
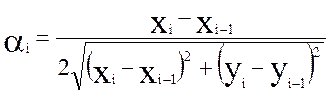( 2.1.)
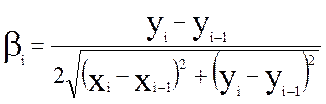
Координаты центров радиусов закруглений можно выразить через значение размеров, координаты узловых точек и направляющие косинусы, примыкающих к данной узловой точке прямолинейных участков (рис. 2.3.).
Здесь и далее использованы известные соотношения геометрии на плоскости /2/.
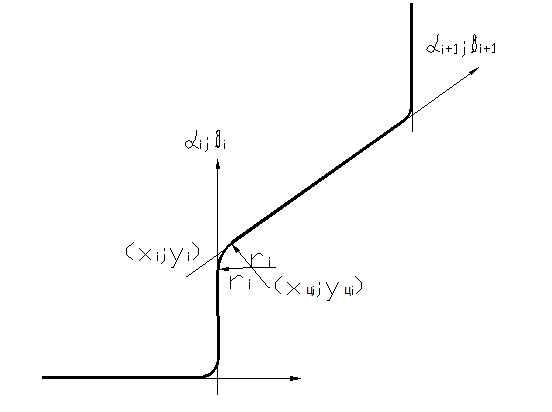
Рис. 2.3. К определению центров радиусов закругления.
Определение центров радиусов закруглений х и у производится согласно формулам
(2.2.)
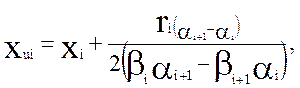
На рис. 2.4. представлена схема к определению координат х , у ; х , у Координаты точек сопряжения радиусов закруглений и прямолинейных участков определяются по формулам
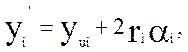
( 2.3.)
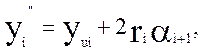
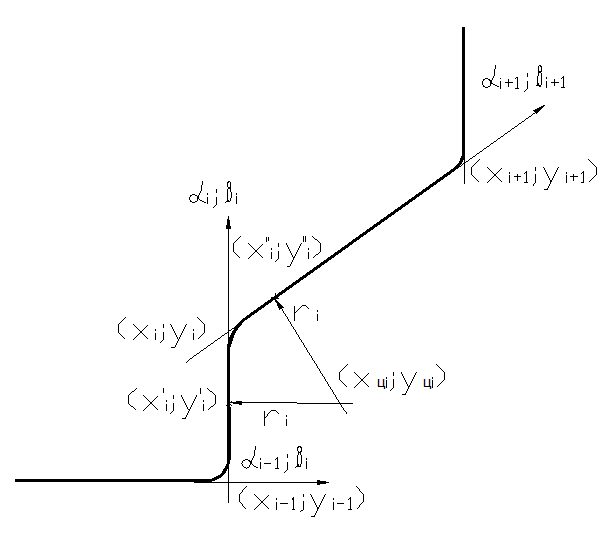
Рис. 2.4. К определению координат точек сопряжения радиусов закругления и прямолинейных участков контура
На рис. 2.5. и 2.6. представлены схемы к аналитическому определению длин дуг сопряжения и координаты их центров тяжести
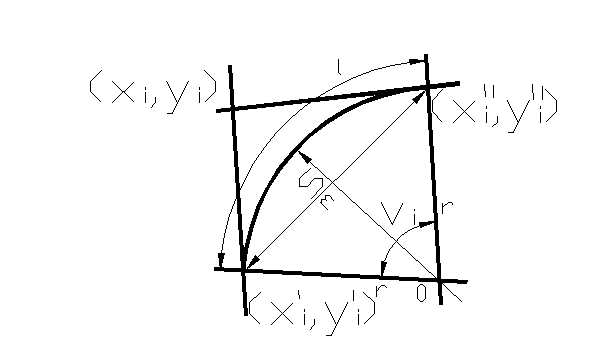
Рис. 2.5. К определению длин дуг
Ниже приведены формулы для определения ℓi , γi , mi (см. рис. 2.5.)
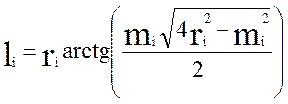
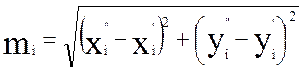(2.4)
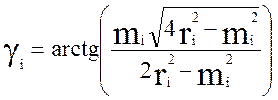
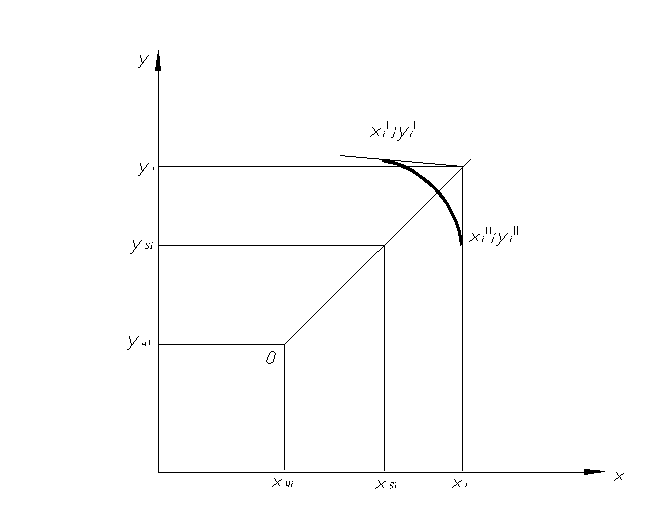
Рис. 2.6. К определению координат центра тяжести дуг
Координаты центров тяжести дуг сопряжения х , у находим по координатам узловых точек х , у , координатам центра радиуса закругления х , у и расстояние центра радиуса закругления до центра тяжести дуги ОS (рис. 2.6.).
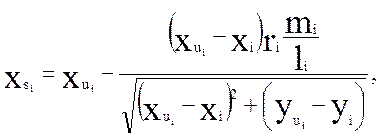
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.