[1]; w - коэффициент продольного изгиба, для гибкости участка элемента расчетной длины lр=1,25.а=1,25.S/6=1,25.32,1/6=6,69 м, при l=90>70 определяемый по формуле:
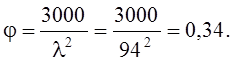
wм – коэффициент, определяемый по формуле:
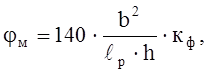
где кф=2,54- коэффициент принимаемый по табл.2 прил.4 [1].
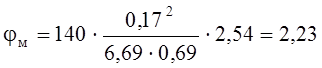
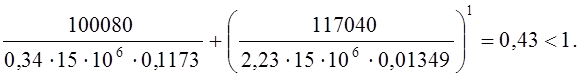
Проверка прочности клеевых швов на скалывание.
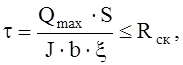
где
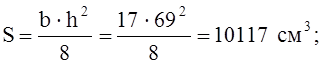
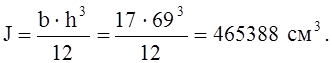
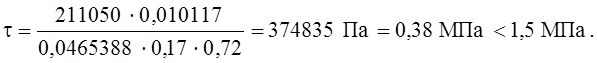
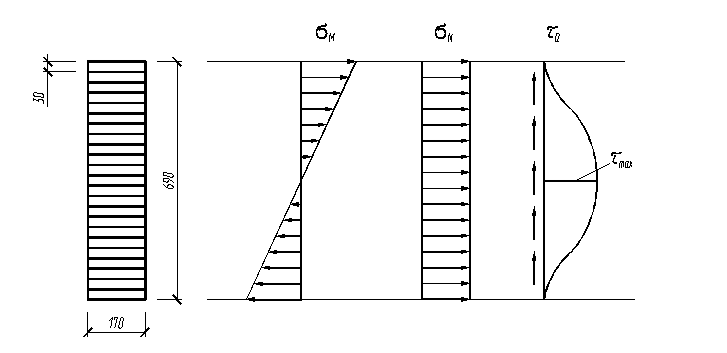
Высоту накладки находим из условия работы торца на смятие от продольной силы N.
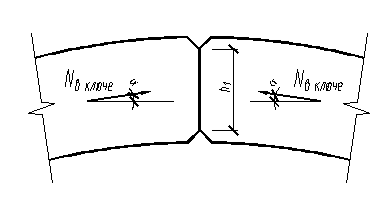
Рис. 4.1. К определению высоты накладки
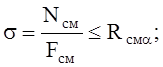
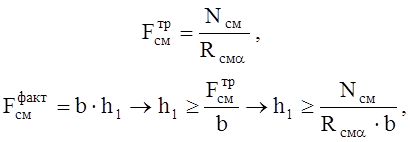
где
Rсмa - расчетное сопротивление древесины смятию под углом a к направлению волокон определяется по формуле:
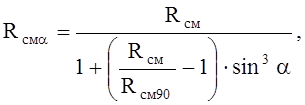
где
a =208329 - угол смятия.
Rсм90= 3 МПа – смятие поперёк волокон, табл.3 [1].
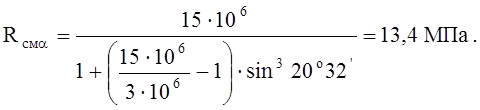
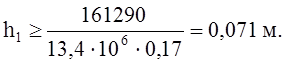
принимаем h1=59см.
Накладка работает на изгиб от поперечной силы Q, возникающей от несимметричного загружения снеговой нагрузкой:
Накладку рассматриваем как балку (см. рис. 4.2), опорами которой являются ряды болтов.
Максимальный момент в накладке:
где
- расстояние между внутренними рядами болтов. Диаметр болтов
принимаем 16 мм, тогда расстояние расстановки болтов:
S1/7d/112 мм - принимаем 120 мм;
S2/3,5d/56 мм;
S3/3d/48 мм.
=2.S1=2.0,12=0,24
м.
Требуемый момент сопротивления накладки:
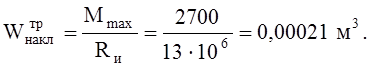
Зададимся толщиной накладки d/4d=4.16=64 мм, принимаем 75 мм.
Фактический момент сопротивления накладки:
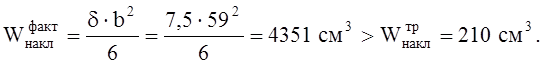
Определим усилия R1 и R2, приходящиеся на один ряд болтов.
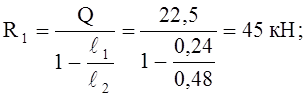
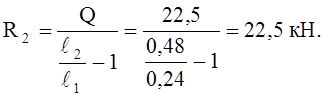
Определим количество болтов в одном ряду:
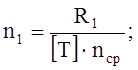
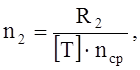
где
[T] – наименьшая несущая способность одного болта, определённая из условий работы болта на изгиб, а древесины под болтами на смятие.
На смятие:
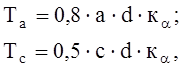
где с=17 см – толщина среднего элемента (арки).
а=7,5 см – толщина крайних элементов (накладок);
d=1,6 см – диаметр болта;
кa=0,9 – коэффициент, определённый по табл.19 [1].
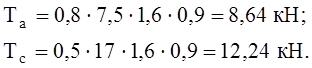
На изгиб:
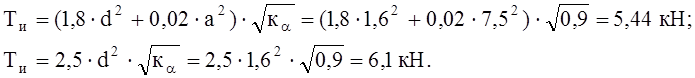
Величина несущей способности болта [T]=5,44 кН.
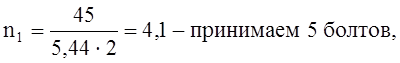
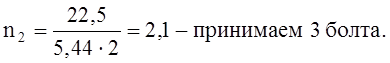
Расстановка болтов показана на рис.4.2.
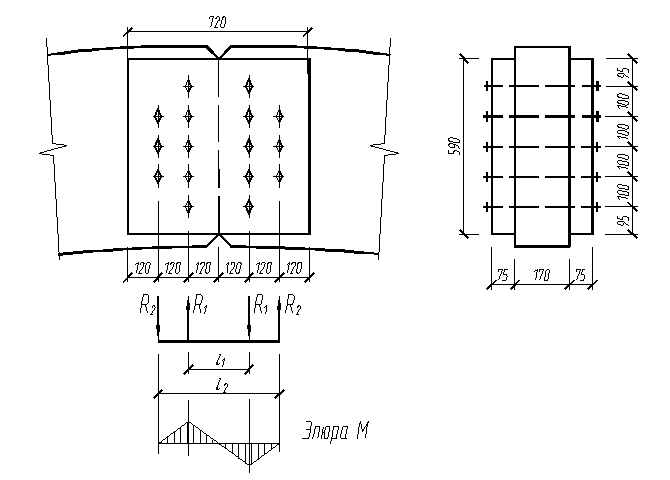
Рис.4.2. Коньковый узел арки
Распор воспринимает затяжка, которая работает на растяжение. Затяжку выполняем из круглой стали. Требуемую площадь сечения определим по формуле:
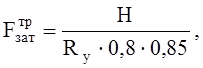
где
Ry=235 МПа – расчетное сопротивление стали С245 растяжению, сжатию и изгиб, табл. 51 [3];
0,8 – коэффициент, учитывающий ослабления в затяжке;
0,85 – коэффициент, учитывающий способ крепления;
Н – суммарный распор от постоянной и снеговой нагрузки:
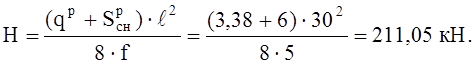
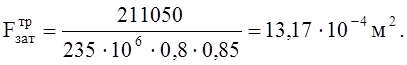
Так как
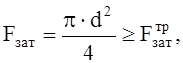
следовательно:
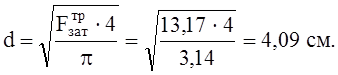
Принимаем d=42
мм, с 
Поверка прочности затяжки:
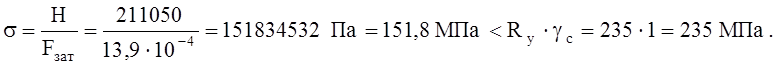
Прочность затяжки обеспечена.
Поверка гибкости затяжки.
где
[l]=400 – предельная гибкость;
r – радиус инерции затяжки:
r=0,25.d=0,25.4,2=1,05 см;
=3
м- расчетная длина затяжки, равная расстоянию между подвесками:
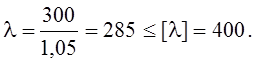
Затяжка крепится к арке
в опорном узле хомутом, состоящим из двух ветвей круглой стали с нарезкой на
концах и траверсы. Требуемая площадь сечения нетто каждой ветви:
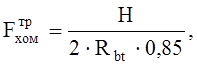
где
Rbt=170 МПа – расчетное сопротивление растяжению болта, табл. 58*[3];
0,85 – коэффициент, учитывающий неравномерность натяжения хомута.
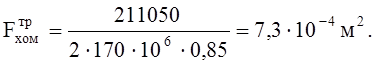
Так как
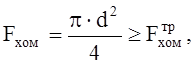
следовательно:
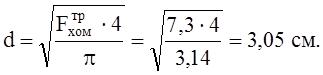
Принимаем d=32
мм, с 
Чтобы воспрепятствовать распрямлению ветвей хомута, между ними ставим распорку из круглой стали того же диаметра, привариваемую к ветвям.
Траверса состоит из швеллера, усиленного приваренными к полкам планками из полосовой стали сечением 10380 мм. Для обеспечения жесткости траверсы в вертикальной плоскости к стенкам швеллера приваривается два уголка 10038 мм. Для траверсы принимаем сталь С245 с Ry=240 МПа (t=2420мм).
Требуемую высоту швеллера определяем из условия смятия древесины арки под траверсой:
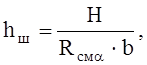
где
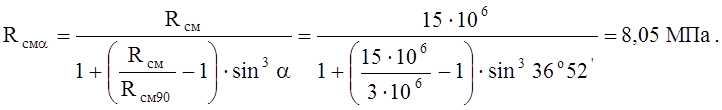
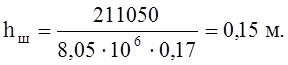
Принимаем швеллер №20 с F1=23,4 см2, J1=113 см4, zo=2,07 см.
Траверсу рассчитываем как балку на двух опорах (ветви хомута) работающую на изгиб от распора, равномернораспределенного по ширине арки. Расчетная схема представлена на рис.5.1.
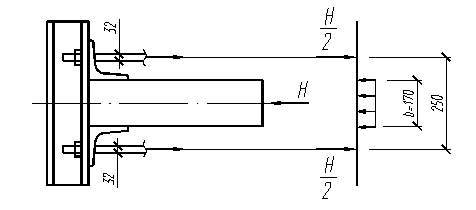
Найдем расчетный пролет траверсы:
Максимальный изгибающий момент в траверсе:
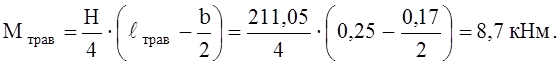
Определим геометрические характеристики сечения траверсы (рис.5.2).
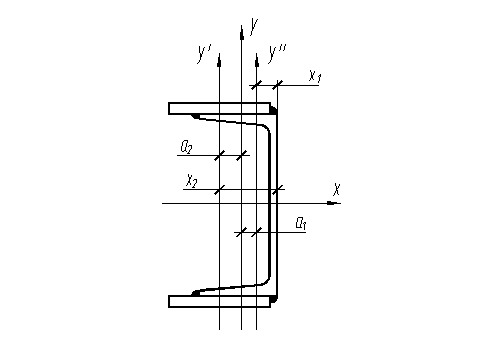
Рис.5.2. Сечение траверсы
Расстояние от наружной грани швеллера до его центра тяжести х1=zо=2,07 см. Планки приварены к полкам швом с катетом 8мм. Тогда расстояние от центра тяжести планок до наружной грани стенки швеллера:
Площадь сечения планок:
Статический момент всего сечения относительно оси у'', проходящей через центр тяжести швеллера:
Расстояние от центра тяжести всего сечения до оси y'':
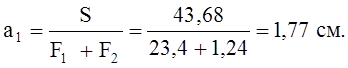
Расстояние между центрами тяжести планок и всего сечения:
Момент инерции всего сечения относительно оси у:
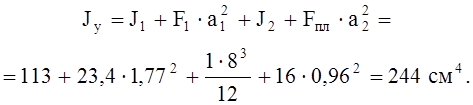
Наибольшее расстояние от оси у до крайнего волокна сечения:
Наименьший момент сопротивления сечения:
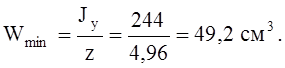
Проверим прочность траверсы:
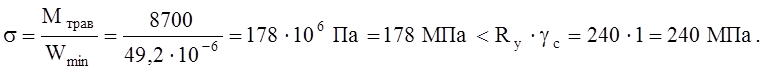
Прочность траверсы обеспечена.
В середине затяжки устраивается стык. Стык выполняется в виде стальных планок с закрепленными в них валиками на которые надеваются петлевидные концы затяжки (рис.5.3). Толщину планки принимаем dпл=10 мм..
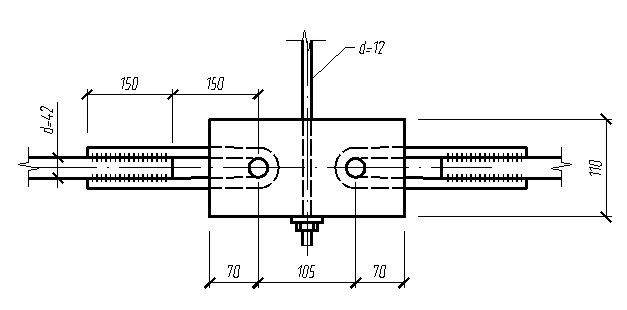
Валики работают на изгиб, как балка на двух опорах (планках).
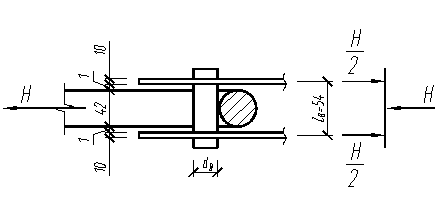
Рис.5.4. Расчетная схема валика
Расчетный пролет валика:
Максимальный изгибающий момент в валике:
Требуемый момент инерции:
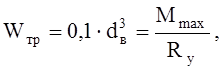
тогда
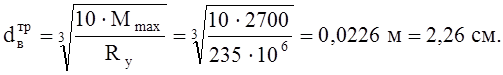
принимаем dв=34 мм.
Принимаем размеры планки исходя из правил расстановки болтов:
принимаем 
принимаем 
Проверим прочность планки на смятие:
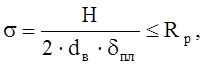
Rbt=327 МПа – расчетное сопротивление стали С245 на смятие, табл. [3].
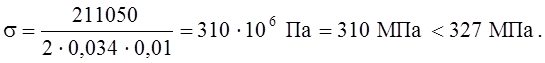
Проверим прочность планки на растяжение:
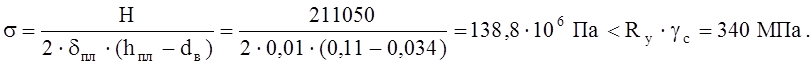Прочность
планки обеспечена.
Определение расчетных усилий в стойке. Нагрузки действующие на стойку показаны на рис. 6.1.
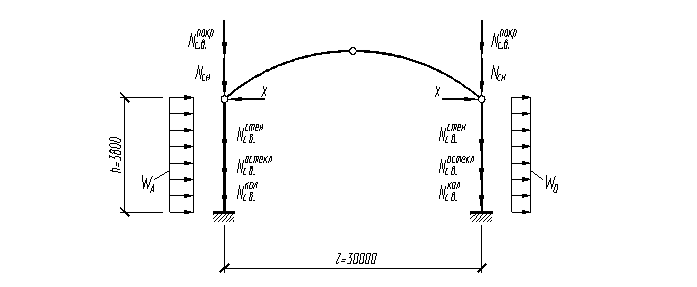
в стойке
Активная и пассивная составляющая ветрового давления:
где
=0,3 кПа – нормативное значение ветрового давления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
