![]() всегда должна быть
соединена с вертикальной линией
всегда должна быть
соединена с вертикальной линией![]() Аналогично,
горизонтальная линия
Аналогично,
горизонтальная линия![]() (отказ всех элементов
системы - самая нижняя ветвь) всегда должка быть соединена с вертикальной линией
(отказ всех элементов
системы - самая нижняя ветвь) всегда должка быть соединена с вертикальной линией![]() (отказ система). О других ветвях дерева мокко судить, лишь зная функциональные
взаимосвязи между элементами системы. Число ветвей полного дерева решений равно
(отказ система). О других ветвях дерева мокко судить, лишь зная функциональные
взаимосвязи между элементами системы. Число ветвей полного дерева решений равно
![]() где
где![]() число элементов (подсистем) системы.
число элементов (подсистем) системы.
4.1. Последовательная система
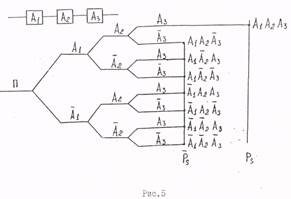
Пусть элементы системы функционируют
последовательно (рис.5). ![]()
|
|
|
|
При последовательном функционировании элементов системы событие отказа хотя бы одного из элементов ведёт к отказу системы в целом, поэтому вероятность неработоспособности Работоспособность системы (рис.5) имеет значение:
|
Полное дерево последовательной системы |
4.2. Параллельная система
Если элементы![]() функционируют
параллельно и если считать, что система работоспособна, если действует хотя бы
один элемент, то полное дерево решений следующее (рис.6).
функционируют
параллельно и если считать, что система работоспособна, если действует хотя бы
один элемент, то полное дерево решений следующее (рис.6).
При параллельном функционировании элементов система неработоспособна, если не действует ни один элемент.
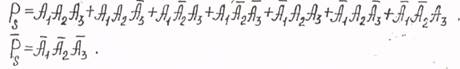
Полное дерево параллельной системы
4.3. Простое дерево решений
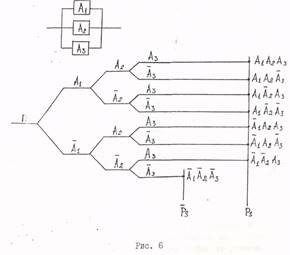
В реальной практике и при решении учебных задач обычно используется простое дерево решений, логику процесса упрощения полного дерева решений проще всего рассмотреть на базе выражений
Выражение содержит семь слагаемых. Если сгруппировать второе слагаемое с третьим, четвертое с пятым, а шестое с седьмым, то получим:
|
|
поскольку![]() Математически это означает, что сумма вероятностей данных шести слагаемых не
зависит от состояния элемента
А3. Технологически - если в последовательной системе откажет какой-либо элемент, то система
неработоспособна независимо от состояния последующих элементов.
Математически это означает, что сумма вероятностей данных шести слагаемых не
зависит от состояния элемента
А3. Технологически - если в последовательной системе откажет какой-либо элемент, то система
неработоспособна независимо от состояния последующих элементов.
После первой стадии упрощения полное дерево последовательной системы упростится (рис.7).
Выражение при этом упростится к виду:
|
|
Вторая стадия упрощения выполняется на базе внракения Объединял третье и четвёртое слагаемые, имеем:
![]()
Ветвь ПА1 не зависит от состояния элемента![]() . Итак, если ветвь дерева решений последовательной системы имеет хотя бы одно отклонение вниз, то эту ветвь можно
соединить с вертикальной линией
. Итак, если ветвь дерева решений последовательной системы имеет хотя бы одно отклонение вниз, то эту ветвь можно
соединить с вертикальной линией ![]() сразу после такого отклонения (рис.8).
сразу после такого отклонения (рис.8).
Дерево последовательной системы после первой стадии упрощения
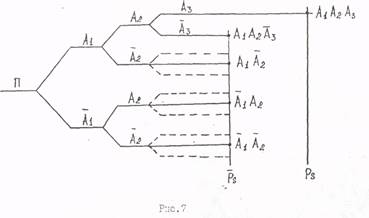
Простое дерево трёхэлементной последовательной системы
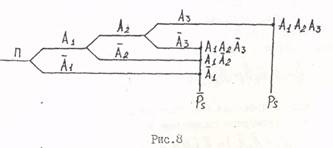
На базе простого дерева решений неработоспособность (ненадёжность) трехэлементной последовательной системы имеет,
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.