Безопасность жизнедеятельности \ Безопасность жизнедеятельности

Анализ безопасности в технических системах, страница 2

3.2. Параллельное функционирование подсистем (элементов)

Вероятность работоспособности (надёжность) системы из N параллельно функционирующих подсистем равна сумме работоспособностей (надёжностей) этих подсистем, считая события успехов (безотказной работы) совместными событиями:



Вероятность неработоспособности (ненадежность) системы из  л/ параллельных подсистем равна произведению неработо способностей (ненадёжностей) этих подсистем:



Частные случаи:













3.3.  Комбинированные системы

При анализе работоспособности систем с комбинированными функциональными связями, систему разбивают на блоки подсистем с выделением более простых связей.  Такому упрощению легко поддаются последовательно-параллельные и параллельно-последовательные системы.   Системы   с зависимым функционированием (сложные системы) будут рассмотрены при анализе дерева решений, где методы вычисления работоспособности менее громоздки и более доступны.

3.3.1. Последовательно-параллельные системы

Рассмотрим последовательно-параллельную систему (рис.2).

Разбивая систему на три последовательных подсистемы А,В,С, вычисляя работоспособности параллельных систем при N=2 (подсистема A ) и    N=3 (подсистема B ),  вычисляют затем работоспособность последовательной системы при N=3.

Пример последовательно-параллельной системы




тогда

При этом

Для корректных, упрощённых оценок лучше всего ввести ненадёжность элемента, тогда

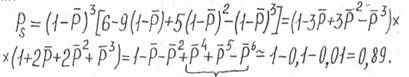
Надёжность системы несколько ниже надёжности отдельного элемента.

4. Анализ работоспособности на базе дерева решения.

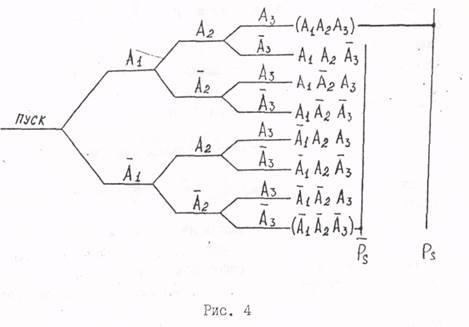
Полное дерево решений представляет собой разновидность дерева событий. Они обладают одной и той же логикой построения ветвей. Разница лишь в одном - в основе дерева событий всегда лежит событие отказа, а в основе дерева решений - команда "Пуск". Рассмотрим дерево решений для системы, содержащей три элемента А1,А2,А3 (рис.4).

Полное дерево решений трёхэлементной системы

Логика построения дерева проста и наглядна (рис.4). После команды "Пуск" элементе/сможет функционировать успешно Дсобытие успеха) с надёжностью J\. или нщункционировать (событие отказа) с ненадёжностью. В свою очередь, при функционирующем (нефункционирующем) элементе, элементтоже имеет две возможности: функционировать с надёжностью  (ответвление вправо-вверх) и нефункционировать с ненадежностью  (ответвление вправо-вниз). Элемент  также имеет две возможности:    А3иА3  - успешно функционировать и отказать. Эти возможности элементав сочетании с возможностями элементовпородят восемь ветвей дерева решений, причём вероятность функционирования системы по каждой ветви есть произведение событий на этих ветвях. Вероятность успешного функционирования системы в целом (работоспособность, ) есть сумма вероятностей событий ведущих к успешной работе, а неработоспособность,   - сумма вероятностей событий, ведущих к отказу. Ясно, что самаяверхняя ветвь с вероятностью(успешное функционирование всех элементов системы) всегда ведёт к успешной работе-системы в целом, иначе, событие есть составная часть 'события    и горизонтальная линия, имеющая произведение

Скачать файл