Алгебра 11 класс. Тема: Интеграл и его применение
Цель данного теста — проверить, умеет ли учащийся:
¾ находить первообразную заданной функции с использованием таблицы первообразных и правил нахождения первообразных (с. 71);
¾ применять формулу Ньютона–Лейбница к вычислению определенного интеграла;
¾ вычислять площадь криволинейной трапеции с помощью интеграла.
Вариант 1
Записывая ответы на задания теста, обведите буквы, отвечающие
утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие
утверждениям, которые вы считаете неправильными. Например, если вы считаете
правильными утверждения А и В, а неправильными — утверждения Б и Г,
запишите 
. Если хотя бы одна буква из
4-х будет не отмечена, задание считается невыполненным.
1. Задана функция F (x) = 2х3. Учитывая, что функция F (x) является первообразной для функции f (x), если F¢(x) = f (x), выберите правильное утверждение.
–А. (2х3)¢ = 3х2.
–Б. Заданная функция является первообразной для функции f (x) = 3х2.
+В. Заданная функция является первообразной для функции f (x) = 6х2.
–Г. Заданная функция является первообразной для функции f (x) = 2х2.
2. Известно,
что для функции f (x) =
хa(a ¹ –1) все первообразные имеют вид F (x)
= 
+ С,
где С — произвольное число.
Выберите правильное утверждение.
–А. Для функции х3 первообразной является х4 + С.
–Б. Для функции х3 первообразной является 3х2 + С.
–В. Для функции х3 первообразной является 
+ С.
+Г. Для функции х3 первообразной является 
+ С.
3. Известно, что 
= F
(b) – F (a), где F (x)
— любая первообразная функции f
(x). Зная, что одной из
первообразных функции х2 является 
, выберите правильное
утверждение.
+А. 
= 
– 
.
–Б. = – .
–В. = + .
–Г. = .
4. Для функции f (x) = х2 + cos х ищут первообразную. Пользуясь таблицей первообразных (с. 71), отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Первообразной для заданной функции является сумма первообразных для функций х2 и cos x.
–А. Первообразной для заданной функции является разность первообразных для функций х2 и cos x.
+Б. Для
функции х2 первообразной является 
.
–Б. Для
функции х2 первообразной является 
.
+В. Для функции соs х первообразной является sin x.
–В. Для функции соs х первообразной является – sin x.
+Г. Все первообразные заданной функции можно записать так:
F (x) =
+ sin x +
С.
–Г. Все первообразные заданной функции можно записать так:
F (x) =
+ sin x
+ С.
5. Вычисляют
интеграл 
. Пользуясь тем, что
= F (x)
= F (b) – F (a),
где F (x) — любая первообразная функции f (x), отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Постоянный множитель 3 можно вынести за знак интеграла.
–А. Если
постоянный множитель 3
вынести за знак интеграла, то получим выражение 3
.
+Б. 
= 
.
–Б. = 
.
+В. = 
–
.
–В. = +
.
+Г. = 18
.
–Г. = 20.
6. Вычисляют площадь криволинейной трапеции, выделенной на рисунке
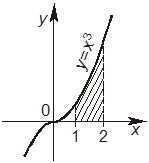
Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Заданная криволинейная трапеция ограничена прямыми x = 1, x = 2, y = 0 и графиком функции y = x3.
–А. Площадь заданной фигуры
можно вычислить по формуле 
.
+Б. Площадь заданной фигуры
можно вычислить по формуле 
.
–Б. Площадь заданной фигуры
можно вычислить по формуле 
.
+В. = .
–В. = .
+Г. Площадь
заданной криволинейной трапеции равна 3
.
–Г. Площадь заданной криволинейной трапеции равна 5.
7. Для функции f (x) = 4х3 + 2х ищут первообразную, график которой проходит через точку М (1; 4). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Все первообразные заданной функции можно
записать так:
F (x) = 4 × + 2 ×
+ C,
где C — произвольная константа.
–А. Все первообразные заданной функции можно
записать так:
F (x) = 4 × + 2 ×.
+Б. Все первообразные заданной функции можно записать так: F (x) = х4 + х2 + С, где С — произвольная константа.
–Б. Все первообразные заданной функции можно записать так: F (x) = 4х4 + х2 + С, где С — произвольная константа.
+В. Если график первообразной проходит через точку М (1; 4), то F (1) = 4.
–В. Если график первообразной проходит через точку М (1; 4), то F (4) = 1.
+Г. Если график первообразной проходит через точку М (1; 4), то F (х) = х4 + х2 + 2.
–Г. Если график первообразной проходит через точку М (1; 4), то F (х) = х4 + х2 – 2.
8. Рассматривают интеграл 
. Отметьте, какие из следующих четырех утверждений
правильные, а какие — неправильные.
+А. Функцию, которая стоит под знаком интеграла, можно записать так: 3х2 – 2х–3.
–А. Функцию, которая стоит под знаком интеграла, можно записать так: 3х2 + 2х–3.
+Б. 
= 3
–2
.
–Б. = 3+2.
+В. = х3
+ 
.
–В. = х3 – .
+Г. = 62
.
–Г. = 63.
9. Вычисляют площадь фигуры, ограниченной линиями:
y = sin
2x, y =
0, х = 
, х = 
. Отметьте, какие из
следующих четырех утверждений правильные, а какие — неправильные.
+А. Заданная
фигура изображается так:
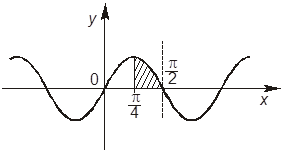
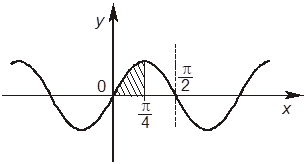
–А. Заданная фигура изображается так:
+Б. Площадь заданной фигуры можно
вычислить по формуле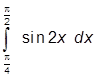 
.
–Б. Площадь заданной фигуры можно
вычислить по формуле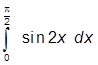 
.
+В. = –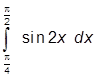
cos 2x
.
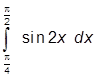–В. = cos 2x.
+Г. Число,
которое выражает площадь заданной фигуры, равно .
–Г. Число,
которое выражает площадь заданной фигуры, равно 
.
10. Тело движется из начала координат прямолинейно вдоль оси х в течение 8 секунд, причем его скорость* изменяется по формуле v (t) = 10 – 2t (единица измерения скорости — м/сек). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. При
движении тела в течение а
секунд его координата будет изменяться по формуле х (t)
= 
.
–А. При
движении тела в течение а
секунд его координата будет изменяться по формуле х (t)
= 
.
+Б. Через 8 секунд тело будет находиться в точке с координатой 16 единиц
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
