Отметьте, какие из приведенных четырех утверждений правильные, а какие — неправильные.
+А. Данное
неравенство равносильно неравенству log
log
x > log 2.
–Б. Данное неравенство равносильно неравенству log x < 2.
–В. Данное неравенство равносильно неравенству x > 
.
+Г. Решением данного неравенства являются все
значения 0 < x < .
4-й уровень
10. Задано
уравнение log
x = x
– 10. Отметьте, какие из приведенных четырех
утверждений правильные, а какие — неправильные.
+А. На области допустимых значений данного уравнения его левая часть является убывающей функцией.
+Б. На области допустимых значений данного уравнения его правая часть является возрастающей функцией.
–В. Если левая часть уравнения является убывающей функцией, а правая — возрастающей, то такое уравнение может иметь два корня.
+Г. Заданное уравнение имеет единственный корень x = 3.
11. Задана
система уравнений 
Отметьте, какие из приведенных четырех утверждений
правильные, а какие — неправильные.
+А. Из
первого уравнения системы следует уравнение
log (–x) +
log y =
3.
+Б. Из первого уравнения системы следует уравнение xy = –8.
–В. Все
решения системы 
являются решениями
заданной системы.
+Г. Заданная
система имеет единственное решение 
12. Задано
неравенство log
(2x + 9) > 0. Отметьте, какие
из приведенных четырех утверждений
правильные, а какие — неправильные.
+А. Данное неравенство равносильно неравенству
log
(2x + 9) > log 1.
–Б. Если x – 2 > 1, то данное неравенство равносильно неравенству 2x + 9 < 1.
+В. Если 0 < x – 2 < 1, то данное неравенство равносильно неравенству 0 < 2x + 9 < 1.
+Г. Решением данного неравенства является x > 3.
Вариант 2
Записывая ответы на задания теста, обведите буквы, отвечающие
утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие
утверждениям, которые вы считаете неправильными. Например, если вы считаете
правильными утверждения А и В, а неправильными — утверждения Б и Г,
запишите 
. Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.
1-й уровень
1. Задана логарифмическая функция y =
log
(3x – 15). Выберите правильное утверждение.
–А. Областью определения данной функции являются все действительные числа.
+Б. Область определения данной функции задается неравенством 3x – 15 > 0.
–В. Область определения данной функции задается неравенством 3x – 15 < 0.
–Г. Область определения данной функции задается неравенством x < 5.
2. Зная, что log
16 — это показатель степени, в которую
надо возвести 2, чтобы получить 16, выберите правильное утверждение.
–А. log 16 = 2.
–Б. log 16 = 3.
–В. log 16 = 5.
+Г. log 16 = 4.
3. Задано
выражение lg(m
n), где m > 0, n > 0. Зная, что
lg (AB) = lg A + lg B (A > 0, B > 0), выберите
правильное утверждение.
–А. lg (m
n) = lg m – lg n.
–Б. lg (m n) = lg m × lg
n.
+В. lg (m n) = lg m + lg n.
–Г. lg (m n) = lg m + lg n.
2-й уровень
4. Задана
логарифмическая функция y = log
x. Отметьте, какие из приведенных четырех утверждений
правильные, а какие — неправильные.
–А. Область определения данной функции задается неравенством x £ 0.
+Б. Данная функция возрастает на всей области определения.
+В. График данной функции имеет вид:
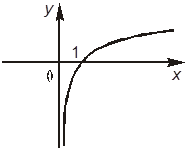
+Г. Множество значений данной функции — все действительные числа.
5. Задано уравнение log
(3x + 2) = 1. Отметьте, какие из приведенных
четырех утверждений правильные, а какие — неправильные.
+А. Из
данного уравнения следует, что 3x
+ 2
= 13
.
–Б. Из
данного уравнения следует, что 3x
+ 2
= 1
.
–В. Данное уравнение имеет единственный корень x = 5.
+Г. Данное
уравнение имеет единственный корень x
= 3
.
6. Задано
неравенство log
(x
– 1) < 2. Учитывая, что логарифмическая функция
с основанием меньше 1 является убывающей
функцией, отметьте, какие из приведенных четырех утверждений правильные, а
какие — неправильные.
+А. Область определения данного неравенства задается неравенством x – 1 > 0.
–Б. Число
2 можно представить так: 2 =
log
.
+В. Если
учесть область определения заданного неравенства,
то из условия следует, что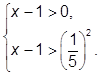 
–Г. Решением заданного неравенства является
промежуток 1 < x < 1
.
3-й уровень
7. Задана функция y =
log
x. Отметьте, какие из приведенных
четырех утверждений правильные, а какие — неправильные.
+А. y = 0 только при x = 1.
–Б. Данная функция возрастает на всей области определения.
–В. log 7 > log 5.
+Г. График
функции y = log x имеет вид:
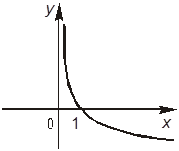
8. Задано уравнение log
(x– 4x – 5) – log (x + 1) =
2. Отметьте, какие из приведенных четырех утверждений правильные,
а какие — неправильные.
–А. Все
корни данного уравнения являются корнями уравнения
log (x
– 4x – 5)(x + 1)
= 2.
+Б. Все
корни заданного уравнения являются корнями уравнения
= 3.
–В. Все
корни заданного уравнения являются корнями уравнения
x – 13x +
14 =
0.
+Г. Корнем заданного уравнения является только одно значение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.