Рекомендації щодо вивчення тем змістовного модулю "Аналітичні способи обробки економічної інформації"

Оцінка ступеня впливу чинників на результативний плоказник
Додавання до кількісного чинника	у1 – у0	Δуа = Δа в0 + Δа Δв = Δа в1 =1×5=5 Δув =  Δв а 0 =1×2=2
	Перевірка: 5+2=7
Додавання до якісного чинника	у1 – у0	Δув = Δ ва0 + Δа Δв = Δ в а 1 =1×3=3 Δуа =  Δ а в0 =1×4=4
	Перевірка: 3+4=7
Розподіл нерозподіленого залишку порівну	у1 – у0	Δуа = Δа в0 + Δа Δв/2 = (1×4) +(1×1) /2=4,5 Δув =  Δв а 0  + Δа Δв/2 = (1×2) +(1×1) /2=2,5
	Перевірка:4,5+2,5=7

Логарифмічний метод

Логарифмічний метод вільний від недоліків методу ланцюгових підстановок, зв'язаних з черговістю факторів, має процедуру з мінімальною кількістю обчислень, застосовується в мультиплікативних моделях. Єдиний недолік його полягає в тому, що у випадках, коли ∆у = 0, ним користуватися не можна. Однак такі випадки в аналізі зустрічаються украй рідко [6].

Наведемо методику розрахунку ∆у на прикладі мультиплікативної моделі, яка у статичній формі має вигляд:

        У =  х_1·  х_{2   ·} х₃ ..... х _п ;                                             (55)

У динамічній формі цю модель можна відобразити наступним чином:

       і _у  = і₁  · і₂  · і₃ ..... · і_п .                                                  (56)

Після логарифмування перемінних рівняння приймає вид

lg і_у  = lg і₁ · lg і₂  ·lg і₃ .....  · lg і_п.                                     (57)

Розділивши обидві частини отриманого рівняння на lg і_у  помноживши на ∆у одержимо:

∆ у_і = ∆у (lg і₁/ lg і _у) +∆у (lg і₂/ lg і _у )+....+ ∆у (lg і_п / lg і _у ).       (58)

В загальному вигляді формула має вид:

∆ у_і = ∆у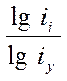.                                                (59)

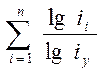∆ у_і = ∆у .                                                (60)

Формула для ∆у являє собою його логарифмічно - пропорційний розподіл по факторах. Саме тому автори методу А. Хумал, В. Федорова і Ю. Єгоров назвали його логарифмічним методом розкладання збільшення ∆у на фактори. Назва виправдовується тим, що отримане правило поділу залишається у силі при будь-якому числі співмножників, а саме: приріст добутку розділяється між перемінними співмножниками пропорційно логарифмам їхніх коефіцієнтів зміни.

Логарифмічний метод передбачає пропорційне розподілення залишку між двома чи більше факторами і дозоляє визначити беззалишковий вплив  чинників на досліджуваний результативний показник.

Сутність логарифмічного методу в тому, що він не потребує  встановлення  черги визначення впливу чинників на результативний показник, а також визначає беззалишковий вплив не лише за  двома, а і за декількома факторами на зміну результативного показника. На практиці цей метод використовується дуже рідко, можливо, по причині труднощів інтерпретації логарифмічних величин.

Інтегральний спосіб

Інтегральний метод застосовується для вивчення  впливу факторів у мультиплікативних і кратних моделях.

Використання цього способу дає можливість більш точно розраховувати вплив факторів, порівняно з способами ланцюгових підстановок, абсолютних і відносних різниць і запобігати неоднозначності оцінки впливу факторів (виключається проблема нерозподіленого залишку).

Основні формули інтегрального методу для  різних моделей:

·  для мультиплікативних моделей:

1)двофакторна модель: С = ХУ

D Сх =Dху₀+ ½ DхDу   або DСх =0,5Dх (у₀ + у₁)

D Су =Dух₀+ ½ DхDу  або  DСх =0,5Dу (х₀ + х₁)

2) три факторна модель: С = Х У Z

D Сх = ½ Dх (у₀z₁+ у₁z₀ ) + 1/3 Dх DуDz

D Су = ½ Dу (х₀z₁+ х₁z₀ ) +1/3 DхDуDz

D С z = ½ D z (х₀ у₁+ х₁у₀ ) +1/3 DхDуDz

3) чотирьох факторна модель: С =ХУZG

D Сх = 1/6 Dх (3у₀ z₀g₀ + у₁ g₀  (z₁+Dz) + g₁ z₀ (у₁  +Dу) + z₁ у₀(g ₁  +Dg )) +

+ ¼  DхDуDzDg    

D Су = 1/6 Dу (3х₀ z₀g₀  + х₁ g₀  (z₁  +Dz) + g₁ z₀(х₁+Dх) + z₁ х₀(g ₁  +Dg )) +

+ ¼  DхDуDzDg    

D С z = 1/6D z (3у₀ х₀ g₀ + х₀ g₁ (у₁  +Dу) + у₁ g ₀(х₁  +Dх) + z₁ у₀(g ₁ +Dg ))+

+ ¼  DхDуDzDg    

D С g = 1/6D g (3у₀ х₀ z₀  + х₀ z₁  (у₁  +Dу) + у₁ z ₀(х₁  +Dх) + х₁ у₀(z ₁  +Dz)) +

+ ¼  DхDуDzDg    

·  для кратних моделей:

С = Х / У

D Сх = Dх / Dу ln | у₁ /  у₀ |

D Су  = D Сзаг - D Сх

·  для змішаних моделей:  С =Х / (У +Z)

D Сх =Dх / (Dу + Dz) ln | у₁ + z₁  /  у₀  + z₀ |

D Су = (D Сзаг - D Сх) / (Dу +Dz) ···Dу

D С z = (D Сзаг - D Сх) / (Dу +Dz) ·D z

Розглянуті технічні прийоми економічного аналізу дають можливість досліджувати будь-які показники підприємства окремо або в комплексі.

(Решту формул розрахунку ступеня впливу чинників на результативний  показник, виражений мультиплікативними і кратними моделями, надано у підручнику  Баканова М.І., Шеремет А.Д.[2 ]).

Для досягнення кінцевої мети аналізу, як правило, використовується  комбінація різних прийомів.

Метод коригуючого коефіцєнту

Метод використовується, коли на результативний показник впливають  чотири і більше факторів, відхилення – позитивне, тип моделі – мультиплікативний.

Процедура розрахунку  впливу факторів надана на  чотирьохфакторній моделі загального виду:  у = а× в×  с ×  к  наступна:

у₁ = а₁× в₁×  с ₁×  к₁ (фактичні)                                       (61)

у₀ = а₀× в₀×  с ₀×  к₀  (базові)                                      (62)

1. Визначення абсолютного відхилення результативного показника  і складових факторів:

у₁  -  у_{0 =}  Dу                                           (63)

а₁  - ау_{0 =}  Dа                                         (64)

в₁  -  в_{0 =}  Dв                                         (65)

с₁  - су_{0 =}  Dс                                         (66)

к₁  -  к_{0 =}  Dк                                         (67)

1.  Визначення відносного відхилення за результативним і  факторним показниками, розраховується як відношення абсолютного відхилення до базисного значення,  відповідно за показниками складає:

за у = ; за а = ; за в = ; за  с = ; за к = ;

2.  Визначення коригуючого коефіцієнта  КК. Розраховується як  відношення відносного відхилення  за результативним  показником до суми відносних відхилень за  чинниками:

КК= (+++)                                      (68)

3.  визначення умовного впливу  факторів на результативний  показник. Для цього абсолютне відхилення за кожним із чинників перемножається