![]()
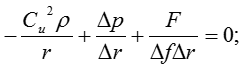
Преобразуем полученное уравнение в следующий вид
Если рассмотреть частицу находящеюся в межвенцовом зазоре (что не меняет физики процесса) тогда: то получим:
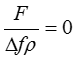

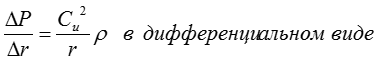
Уравнение радиального равновесия частиц находящихся на линии тока говорит о том , что градиент давления прямо пропорционален квадрату закрутки потока и обратно пропорционален радиусу. Чтобы компенсировать увеличение давления вдоль радиуса необходимо увеличить закрутку потока по радиусу.
Уравнение неразрывности применительно к одномерной и двухмерной модели.
В процессе проектирования решается задача определения проходных площадей сечений проточной части.
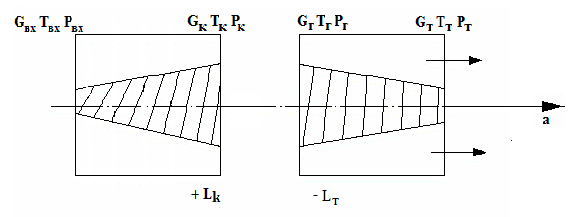
При анализе уравнений для компрессора и турбины компенсировать изменения плотности, сечении происходит за счёт изменения площади проточной части.
Для 2-х мерной модели:
Рассмотрим сопловой аппарат осевой турбины. Известны кинематика и параметры потока на входе и выходе из турбинной решетки а также в самом узком сечении МЛК <горле>. Определить угол выхода потока из турбинной решетки.
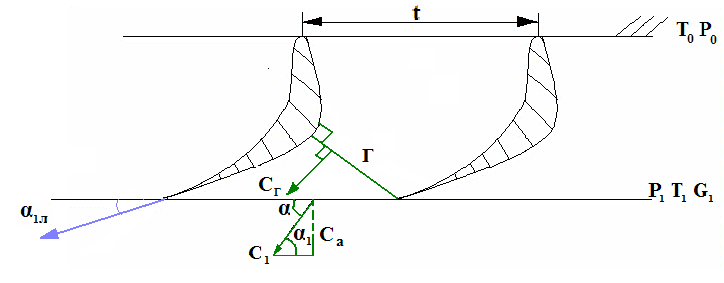
Уравнение неразрывности запишется так:
Gг = G1 => CгρгFг=Са1ρ1F1
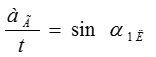
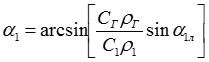

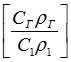
Кинематический угол зависит от угла лопатки на выходе и от режима течения потока
Уравнение энергии в тепловой форме.
При переходе системы из состояния i в состояние i+1 изменение полной энергии системы равно сумме подводимой (отводимой) теплоты и работы. ΔE(i;i+1)= ± Q ± Lтех Изменение полной энергией системы ΔE удобнее рассматривать через изменение: Внутренней энергии: du = CVdT Потенциальной энергии: Кинетической энергии:
![]()
![]()
Тогда при переходе из состояние i в состояние i+1 полная техническая работа
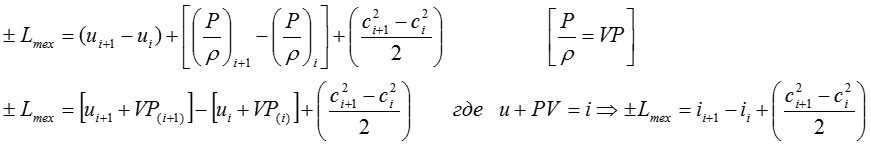
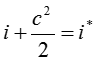
тогда
![]()
Рассмотрим уравнение энергии в тепловой форме применительно к процессу сжатия в компрессоре. В термодинамике подводимая работа положительна, отводимая отрицательна, тогда для компрессора Lтех>0
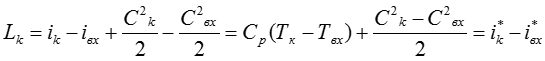
![]()

![]()
к ступени ОК
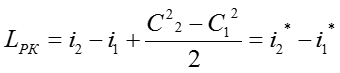
![]()
РК
НА
1
2
2
3

![]()
}
![]()
}
![]()
![]()
T*
![]()
}

T
T*w
Tw
![]()
w
С1
![]()
В относительном движении работа не отводится и не подводится, происходит только поворот потока. Вывод:Уравнение энергии в тепловой форме позволяет произвести оценку температуры, но не возможно сделать оценку эффективности процесса.
Рассмотрим уравнение энергии применительно к осевой турбине и ее ступени
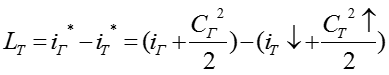
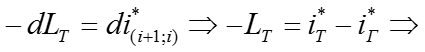
![]()



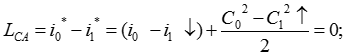

![]()
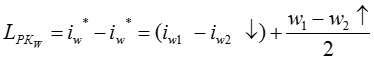
![]()
Уравнение энергии в тепловой форме дает представление о характере изменения температуры. Но не позволяет сделать оценку эффективности процесса т.к. тепло выделившееся в результате сил трения, оставаясь в потоке, пополняет его теплосодержание
Уравнение энергии в механической форме.
Из 1-го закона термодинамики известно, что количества тепла получаемого системой затрачивается на изменение внутренней энергии системы и совершения работы.
Если обозначить через энтальпию i=u+PV тогда
![]()
![]()
![]()
![]()
Подставляем его в уравнение (1) получим:
Из уравнения энергии в тепловой форме
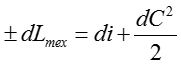
Выражаем di и подставляем его в уравнение (2)

Тепло выделившееся в результате сил трения прямо пропорционально работе затраченной на их преодоление: тогда работа, совершаемая системой равна:
![]()

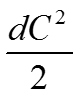
- величина изменения кинематической энергии потока.
Рассмотрим уравнение энергии в механической форме применительно к процессу сжатия и к ступени ОК.
в компрессоре
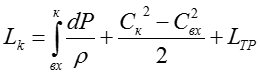
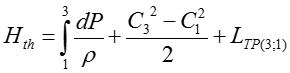
Подводимая работа к ступени расходуется на политропическое сжатие, изменение кинетической энергии и преодоление сил трения.
Подводимая к компрессору работа расходуется на политропическую работу сжатия, изменение кинетической энергии и преодоление сил трения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.