Цифровые автоматы. Синтез автомата для преобразования двоично-десятичного кода с весами 5.2.2.1 в двоично-десятичный код с весами 6.3.2.1, страница 8

Граф автомата Мили по разметке номер 1.

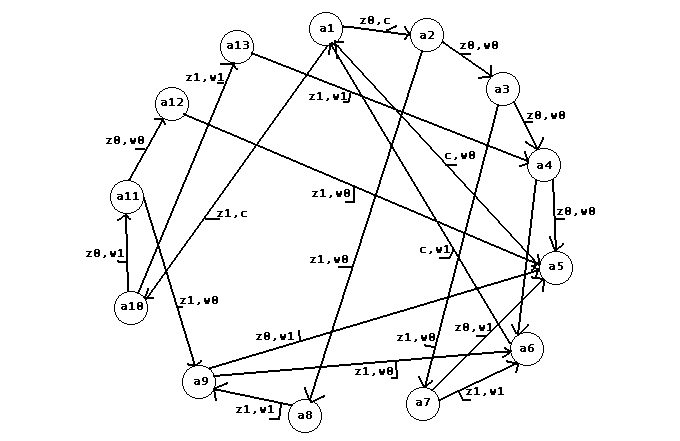
Рис.4

Граф автомата Мили по разметке 2.

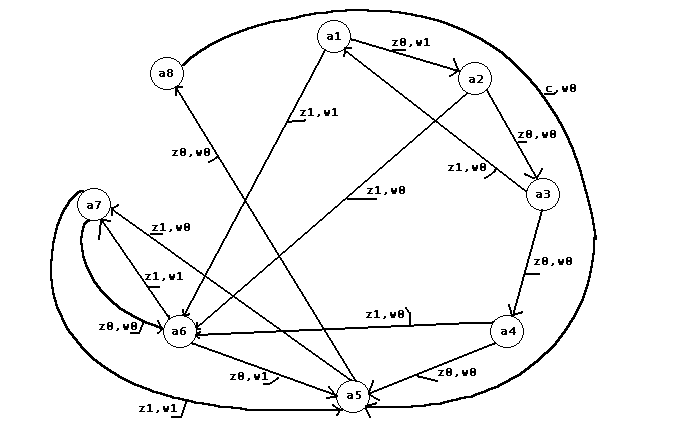
Рис.5

Граф автомата Мура по разметке 3.

Рис.6

2.2 Минимизация числа состояний.

Наименьшим числом состояний обладает автомат Мили полученый по разметке 2. Его мы и будем использовать в следующем этапе абстрактного синтеза. Так как автомат полностью определенный , то используем метод Аумфенкампа-Хона.

B11={a1,a6}  B12={a2,a3,a4,a8}   B13={a7}

B21={a1}  B22={a6}  B23={a2,a3,a4}  B24={a5} B25={a8}  B26={a7}

B31={a1} B32={a6} B33={a2} B34={a3} B35={a4} B36={a5} B37={a8} B38={a7}

Минимизация не дала уменьшения числа состояний. Автомат является минимальным. Ниже представлена таблица переходов автомата, по которой будем производить структурный синтез.

3.  Структурный синтез автомата.

Автомат будем строить на синхронных JK триггерах.  Словарь JK триггера представлен в таблице:

Ниже представлена кодированная таблица преходов выходов автомата: