Рис. 3.3.2
Теперь выкидываем подмножества:
{a1}{a2}{a3}{a4}{a5}{a6}{a7}{a8}{a9}{a10}{a11}{a12,a14}{a13}{a15}
Получили, что каждое состояние встречается в МС-классах только один раз. Причем состояния a12 и a14 совместимы без дополнительных условий, => мы можем представить каждый МС-класс как новое состояние, т.е. мы получили минимальный автомат:
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
a13 |
a14 |
|
|
Z0 |
a2 |
a3 |
a4 |
a5 |
a6 |
a1 |
a8 |
a1 |
a10 |
a6 |
a8 |
a14 |
a7 |
a4 |
|
C |
C |
w0 |
w0 |
w0 |
w0 |
w0 |
w1 |
w0 |
w1 |
w1 |
C |
w1 |
w1 |
|
|
Z1 |
a12 |
a12 |
a9 |
a7 |
a6 |
a1 |
a8 |
a1 |
a11 |
a6 |
a8 |
a13 |
a10 |
a9 |
|
C |
C |
w0 |
w0 |
w0 |
w0 |
w0 |
w1 |
w0 |
w1 |
w1 |
w0 |
w1 |
w1 |
4.Структурный синтез автомата
4.1.Построение булевых функций
На рисунке 4.1.1 приведена кодировка состояний автомата, а на рисунках 4.1.2 и 4.1.3 – кодировка входных и выходных сигналов соответственно.
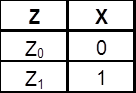 |
 |
|
Ai |
Q1 |
Q2 |
Q3 |
Q4 |
|
a1 |
0 |
0 |
0 |
1 |
|
a2 |
0 |
0 |
1 |
0 |
|
a3 |
0 |
0 |
1 |
1 |
|
a4 |
0 |
1 |
0 |
0 |
|
a5 |
0 |
1 |
0 |
1 |
|
a6 |
0 |
1 |
1 |
0 |
|
a7 |
0 |
1 |
1 |
1 |
|
a8 |
1 |
0 |
0 |
0 |
|
a9 |
1 |
0 |
0 |
1 |
|
a10 |
1 |
0 |
1 |
0 |
|
a11 |
1 |
0 |
1 |
1 |
|
a12 |
1 |
1 |
0 |
0 |
|
a13 |
1 |
1 |
0 |
1 |
|
a14 |
1 |
1 |
1 |
0 |
Рис. 4.1.1
Рис. 4.1.2 Рис. 4.1.3
На рисунке 4.1.4 изображена таблица построения булевых функций для JK-триггера, а на рисунке 4.1.5 – для T-триггера (это необходимо для более простой реализации на СИС и БИС).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.