Информатика и выч. техника \ Теория автоматов

Синтез автомата для преобразования двоично-десятичного кода с весами 5.4.2.1 в двоично-десятичный код с весами 6.3.2.1

Страницы работы

16 страниц (Word-файл)
Посмотреть все страницы
Скачать файл

Фрагмент текста работы

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Вычислительной Техники

КУРСОВАЯ РАБОТА

 по дисциплине “Теория автоматов”

СИНТЕЗ АВТОМАТА

Выполнил:

Принял:

Нижний Новгород

2002 г.

Содержание

1. Цель работы........................................................................................................................................... 3

2. Таблицы функционирования и соответствия.......................................................................................... 3

3. Абстрактный синтез автомата................................................................................................................. 4

3.1. Информативное нагруженное дерево, соответствующие ему графы и таблицы переходов............. 4

3.2. Разметка вход-выходных слов......................................................................................................... 6

3.3. Минимизация автомата.................................................................................................................... 8

4. Структурный синтез автомата................................................................................................................. 9

4.1. Построение булевых функций.......................................................................................................... 9

4.2. Раздельная минимизация................................................................................................................ 9

4.3. Совместная минимизация.............................................................................................................. 11

4.4. Реализация на элементах малой степени интеграции (К155)......................................................... 12

4.5. Реализация с использованием элементов средней степени интеграции (дешифратор К155)........ 13

4.6. Реализация на элементах большой степени интеграции (ПЗУ)...................................................... 15

1.  Цель работы

Синтезировать автомат для преобразования двоично-десятичного кода с весами 5, 4, 2, 1, который поступает на вход в последовательной форме, начиная со старшего разряда, в двоично-десятичный код с весами 6, 3, 2, 1, который снимается с выхода в последовательной форме, начиная со старшего разряда. Провести синтез абстрактного автомата Мили и Мура по первой и второй стратегии. Для каждого автомата привести таблицы переходов и выходов, а также графы работы. По автомату с наименьшим числом внутренних состояний построить структурный автомат. Для структурного автомата провести минимизацию. Провести синтез комбинационной схемы автомата на микросхемах малой, средней и большой степени интеграции серии К155.

2. Таблицы функционирования и соответствия

Таблица функционирования для синтезируемого автомата:

N

x1

5

x2

4

x3

2

x4

1

y1

6

y2

3

y3

2

y4

1

0

0

0

0

0

0

0

0

0

1

0

0

0

1

0

0

0

1

2

0

0

1

0

0

0

1

0

3

0

0

1

1

0

0

1

1

4

0

1

0

0

0

1

0

1

5

0

1

0

1

0

0

1

1

6

0

1

1

0

0

1

1

1

7

1

0

1

0

1

0

0

1

8

1

0

1

1

1

0

1

0

9

1

1

0

0

1

1

0

0

Автоматное отображение не реализуется, следовательно необходимо вводить пустые буквы во входные и выходные слова.

Таблица соответствия для автомата:

Z доп

W *

z0 z0 z0 z0 c

c w0 w0 w0 w0

z0 z0 z0 z1 c

c w0 w0 w0 w1

z0 z0 z1 z0 c

c w0 w0 w1 w0

z0 z0 z1 z1 c

c w0 w0 w1 w1

z0 z1 z0 z0 c

c w0 w1 w0 w1

z0 z1 z0 z1 c

c w0 w1 w1 w0

z0 z1 z1 z0 c

c w0 w1 w1 w1

z1 z0 z1 z0 c

c w1 w0 w0 w1

z1 z0 z1 z1 c

c w1 w0 w1 w0

z1 z1 z0 z0 c

c w1 w1 w0 w0

3. Абстрактный синтез автомата

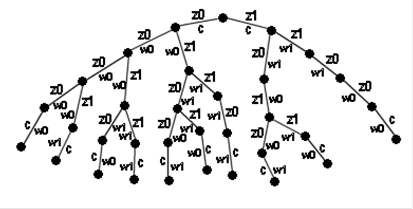
3.1. Информативное нагруженное дерево, соответствующие ему графы и таблицы переходов

Ниже представлено информативное нагруженное дерево, соответствующее синтезируемому автомату:


Граф автомата Мили, синтезированный по таблице соответствия:

              

Совмещенная таблица переходов автомата Мили, синтезированного по таблице соответствия:

a(t)

a1

a2

a3

a4

a5

a6

a7

a8

a9

a10

a11

a12

a13

a14

a15

a16

a17

a18

a19

a20

a21

a22

a23

z(t)

z0

a10

a6

a4

a1

a1

-

a8

a1

a1

a17

a12

a13

a1

a1

a16

a1

a18

a22

a20

a1

a1

a1

a1

c

w1

w0

w0

w0

-

w0

w1

w0

w0

w1

w0

w1

w0

w1

w1

w0

w0

w1

w0

w1

w0

w1

z1

a2

a3

-

-

a1

a7

a9

a1

a1

a11

a15

a14

a1

a1

-

a1

a19

a23

a21

a1

a1

a1

a1

c

w1

-

-

w0

w0

w1

w1

w0

w0

w1

w1

w1

w0

-

w1

w0

w0

w1

w0

w1

w0

w1

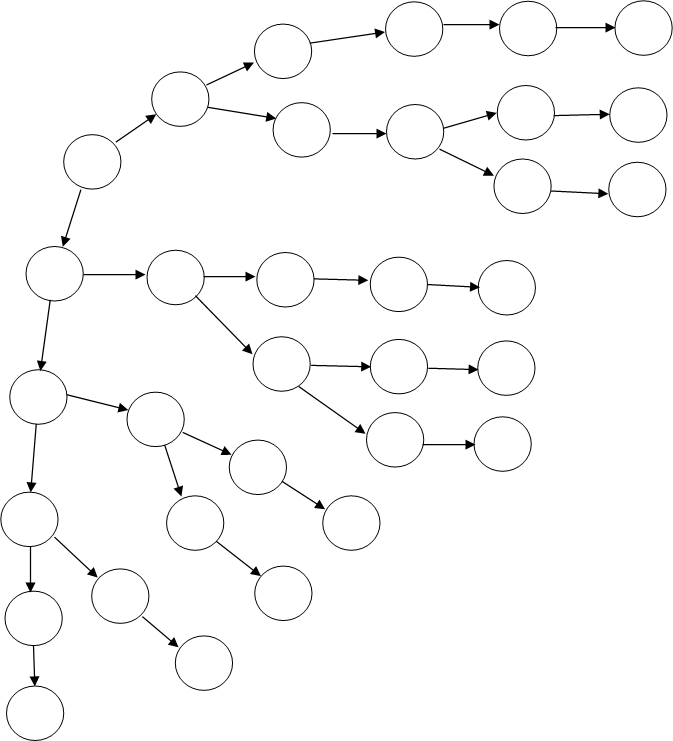
Граф автомата Мура:

 


Совмещенная таблица переходов автомата Мура:

z(t)

c

c

w1

w1

w0

w0

w1

w0

w1

w0

w0

w1

w1

w0

w0

w0

w0

a1

a2

a3

a4

a5

a6

a7

a8

a9

a10

a11

a12

a13

a14

a15

a16

a17

z0

a13

a7

a4

a5

a6

-

-

a11

a10

-

a12

-

a14

a15

a16

a17

-

z1

a2

a3

-

-

a6

-

a8

a9

a10

-

a12

-

a25

a20

a18

a17

-

z(t)

w0

w1

w0

w1

w0

w1

w1

w0

w1

w0

w1

w1

w0

w1

w1

w1

a18

a19

a20

a21

a22

a23

a24

a25

a26

a27

a28

a29

a30

a31

a32

a33

z0

a19

-

a21

a22

-

a24

-

a26

a27

a28

-

a30

-

a32

a33

-

z1

a18

-

a23

a22

-

a24

-

a31

a29

a28

-

a30

-

-

a33

-

3.2. Разметка вход-выходных слов

В данной работе были произведены разметки вход-выходных слов для автоматов Мили и Мура по 1-й и 2-й стратегии. Первая стратегия предполагает немедленное введение нового состояния там, где переход еще не определен, вторая стратегия стремится обойтись старыми состояниями.

Разметка автомата Мили по второй стратегии

z0

z0

z0

z0

C

C

w0

w0

w0

w0

1

2

3

4

5

1

z0

z0

z0

z1

C

C

w0

w0

w0

w1

1

2

3

4

6

1

z0

z0

z1

z0

C

C

w0

w0

w1

w0

1

2

3

7

5

1

z0

z0

z1

z1

C

C

w0

w0

w1

w1

1

2

3

7

6

1

z0

z1

z0

z0

C

C

w0

w1

w0

w1

1

2

8

9

6

1

z0

z1

z0

z1

C

C

w0

w1

w1

w0

1

2

8

9

5

1

z0

z1

z1

z0

C

C

w0

w1

w1

w1

1

2

8

10

6

1

z1

z0

z1

z0

C

C

w1

w0

w0

w1

1

11

12

9

6

1

z1

z0

z1

z1

C

C

w1

w0

w1

w0

1

11

12

9

5

1

z1

z1

z0

z0

C

C

w1

w1

w0

w0

1

11

13

4

5

1

Разметка автомата Мили по первой стратегии

z0

z0

z0

z0

C

C

w0

w0

w0

w0

1

2

3

4

5

1

z0

z0

z0

z1

C

C

w0

w0

w0

w1

1

2

3

4

6

1

z0

z0

z1

z0

C

C

w0

w0

w1

w0

1

2

3

7

8

1

z0

z0

z1

z1

C

C

w0

w0

w1

w1

1

2

3

7

9

1

z0

z1

z0

z0

C

C

w0

w1

w0

w1

1

2

10

11

12

1

z0

z1

z0

z1

C

C

w0

w1

w1

w0

1

2

10

11

13

1

z0

z1

z1

z0

C

C

w0

w1

w1

w1

1

2

10

14

15

1

z1

z0

z1

z0

C

C

w1

w0

w0

w1

1

16

17

18

19

1

z1

z0

z1

z1

C

C

w1

w0

w1

w0

1

16

17

18

20

1

z1

z1

z0

z0

C

C

w1

w1

w0

w0

1

16

21

22

23

1

Совмещенная таблица переходов и выходов для автомата Мили:

a(t)

a1

a2

a3

a4

a5

a6

a7

a8

a9

a10

a11

a12

a13

z(t)

z0

a2

a3

a4

a5

a1

a1

a5

a9

a6

a6

a12

-

a4

c

w0

w0

w0

w0

w1

w1

w1

w0

w1

w1

-

w1

z1

a11

a8

a7

a6

a1

a1

a6

a10

a5

-

a13

a9

-

c

w0

w0

w0

w0

w1

w1

w1

w1

-

w1

w0

-

Разметка автомата Мура по второй стратегии

z1

z1

z0

z0

C

C

w1

w1

w0

w0

1

2

3

4

5

6

z1

z0

z1

z1

C

C

w1

w0

w1

w0

1

2

7

8

9

6

z1

z0

z1

z0

C

C

w1

w0

w0

w1

1

2

7

8

10

11

z0

z0

z0

z0

C

C

w0

w0

w0

w0

1

12

13

14

5

6

z0

z0

z0

z1

C

C

w0

w0

w0

w1

1

12

13

14

10

11

z0

z0

z1

z0

C

C

w0

w0

w1

w0

1

12

13

15

9

6

z0

z0

z1

z1

C

C

w0

w0

w1

w1

1

12

13

15

16

11

z0

z1

z0

z0

C

C

w0

w1

w0

w1

1

12

17

18

10

11

z0

z1

z0

z1

C

C

w0

w1

w1

w0

1

12

17

18

9

6

z0

z1

z1

z0

C

C

w0

w1

w1

w1

1

12

17

19

16

11

Разметка автомата Мура по первой стратегии

z1

z1

z0

z0

C

C

w1

w1

w0

w0

1

2

3

4

5

6

z1

z0

z1

z1

C

C

w1

w0

w1

w0

1

2

7

8

9

10

z1

z0

z1

z0

C

C

w1

w0

w0

w1

1

2

7

8

11

12

z0

z0

z0

z0

C

C

w0

w0

w0

w0

1

13

14

15

16

17

z0

z0

z0

z1

C

C

w0

w0

w0

w1

1

13

14

15

18

19

z0

z0

z1

z0

C

C

w0

w0

w1

w0

1

13

14

20

21

22

z0

z0

z1

z1

C

C

w0

w0

w1

w1

1

13

14

20

23

24

z0

z1

z0

z0

C

C

w0

w1

w0

w1

1

13

25

26

27

28

z0

z1

z0

z1

C

C

w0

w1

w1

w0

1

13

25

26

29

30

z0

z1

z1

z0

C

C

w0

w1

w1

w1

1

13

25

31

32

33

Совмещенная таблица переходов и выходов для автомата Мура:

z(t)

c

c

w1

w1

w0

w0

w1

w0

w1

w0

w1

с

w0

w0

w0

w1

w0

w1

w1

a1

a2

a3

a4

a5

a6

a7

a8

a9

a10

a11

a12

a13

a14

a15

a16

a17

a18

a19

z0

a13

a7

a4

a5

a6

-

-

a10

a6

a11

-

a13

a14

a5

a9

a11

a18

a10

a16

z1

a2

a3

-

-

a6

-

a8

a9

a6

a11

-

a17

a15

a10

a16

a11

a19

a9

-

В итоге, для автомата Мили из 23 состояний получили 13 , а для автомата Мура из 33 состояний – 19.

Из полученных автоматов выберем автомат Мили (с переходом в начальное состояние), как имеющий наименьшее число состояний.

3.3. Минимизация автомата

На данном рисунке приведена диаграмма пар совместимости состояний:

2

X

3

X

X

4

X

X

X

5

X

X

X

X

6

X

X

X

X

X

7

X

X

X

X

X

X

8

X

X

X

X

X

X

X

9

X

X

X

X

X

X

X

X

10

X

X

X

X

X

X

X

X

X

11

X

X

X

X

X

X

X

X

X

X

12

X

X

X

X

X

X

X

X

X

X

X

13

X

X

X

X

X

X

X

X

X

X

X

X

1

2

3

4

5

6

7

8

9

10

11

12

Ниже приведена соответствующая таблица построения МС-классов:

Шаг

Система множеств

0

{a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13 }

1

{a1}, {a2, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13 }

2

{a1}, {a2}, {a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13 }

3

{a1}, {a2}, {a3}, {a4, a5, a6, a7, a8, a9, a10, a11, a12, a13 }

4

{a1}, {a2}, {a3}, {a4}, {a5, a6, a7, a8, a9, a10, a11, a12, a13 }

5

{a1}, {a2}, {a3}, {a4}, {a5}, {a6, a7, a8, a9, a10, a11, a12, a13 }

6

{a1}, {a2}, {a3}, {a4}, {a5}, {a6}, {a7, a8, a9, a10, a11, a12, a13 }

7

{a1}, {a2}, {a3}, {a4}, {a5}, {a6}, {a7}, {a8, a9, a10, a11, a12, a13 }

8

{a1}, {a2}, {a3}, {a4}, {a5}, {a6}, {a7}, {a8}, {a9, a10, a11, a12, a13 }

9

{a1}, {a2}, {a3}, {a4}, {a5}, {a6}, {a7}, {a8}, {a9}, {a10, a11, a12, a13 }

10

{a1}, {a2}, {a3}, {a4}, {a5}, {a6}, {a7}, {a8}, {a9}, {a10}, {a11, a12, a13 }

11

{a1}, {a2}, {a3}, {a4}, {a5}, {a6}, {a7}, {a8}, {a9}, {a10}, {a11}, {a12, a13 }

12

{a1}, {a2}, {a3}, {a4}, {a5}, {a6}, {a7}, {a8}, {a9}, {a10}, {a11}, {a12}, {a13 }

Поскольку автомат является полностью определенным, множество всех МС-классов является минимальным замкнутым покрытием. Следовательно, автомат, полученный путем разметки вход-выходных слов, является минимальным.

4. Структурный синтез автомата

4.1. Построение булевых функций

Ниже изображена таблица построения булевых функций для Т-триггера.

t

t + 1

x

Q1

Q2

Q3

Q4

y

Q1

Q2

Q3

Q4

fQ1

fQ2

fQ3

fQ4

T1

T2

T3

T4

0

0

0

0

0

-

0

0

0

1

0

0

0

a

0

0

0

1

0

0

0

0

1

0

0

0

1

0

0

0

a

b

0

0

1

1

0

0

0

1

0

0

0

0

1

1

0

0

1

a

0

0

0

1

0

0

0

1

1

0

0

1

0

0

0

a

b

b

0

1

1

1

0

0

1

0

0

0

0

0

0

0

0

b

0

0

0

1

0

0

0

0

1

0

1

1

0

0

0

0

0

b

0

b

0

1

0

1

0

0

1

1

0

1

0

1

0

0

0

1

b

0

0

0

1

0

0

0

1

1

1

1

1

0

0

0

a

b

b

b

1

1

1

1

0

1

0

0

0

0

0

1

0

1

b

a

0

a

1

1

0

1

0

1

0

0

1

1

0

1

0

1

b

a

0

1

1

1

0

0

0

1

0

1

0

1

1

0

1

1

1

0

1

a

0

0

0

1

0

1

0

1

1

-

-

-

-

-

-

-

-

-

-

-

-

-

0

1

1

0

0

1

0

0

1

1

b

b

a

a

1

1

1

1

1

0

0

0

0

-

1

0

1

0

a

0

a

0

1

0

1

0

1

0

0

0

1

0

0

1

1

1

0

a

a

1

0

1

1

0

1

0

0

1

0

0

0

1

1

0

0

a

1

0

0

1

0

0

1

0

0

1

1

0

0

1

0

1

0

a

b

1

0

1

1

0

1

0

1

0

0

0

0

0

0

0

0

b

0

0

0

1

0

0

1

0

1

0

1

1

0

0

0

0

0

b

0

b

0

1

0

1

1

0

1

1

0

1

0

1

0

1

0

1

b

a

0

0

1

1

1

0

1

1

1

1

1

0

0

1

a

b

b

1

1

1

1

0

1

1

0

0

0

1

0

1

0

0

b

a

0

0

1

1

0

0

1

1

0

0

1

-

-

-

-

-

-

-

-

-

-

-

-

-

1

1

0

1

0

1

1

1

0

0

1

a

b

0

0

1

1

0

1

1

0

1

1

0

1

0

0

0

1

0

b

b

0

0

1

1

1

1

1

0

0

-

-

-

-

-

-

-

-

-

-

-

-

-

4.2. Раздельная минимизация

Далее следует раздельная минимизация булевых функций для T-триггера.

На рисунках представлены соответствующие карты Карно:

T1

Q2 Q3 Q4

x Q1

000

001

011

010

110

111

101

100

00

0

0

0

0

0

1

0

0

01

1

1

-

0

-

-

-

1

11

1

-

0

0

-

-

-

-

10

1

1

0

0

0

1

0

0

T2

Q2 Q3 Q4

x Q1

000

001

011

010

110

111

101

100

00

0

0

1

0

0

1

1

1

01

1

1

-

0

-

-

-

1

11

1

-

0

1

-

-

-

-

10

0

1

1

1

0

1

1

1

         

T3

Q2 Q3 Q4

x Q1

000

001

011

010

110

111

101

100

00

0

1

1

1

1

1

0

0

01

0

0

-

0

-

-

-

1

11

0

-

1

1

-

-

-

-

10

1

1

1

0

1

1

0

0

T4

Q2 Q3 Q4

x Q1

000

001

011

010

110

111

101

100

00

1

1

1

1

0

1

1

0

01

1

0

-

1

-

-

-

1

11

0

-

1

0

-

-

-

-

10

0

0

0

0

1

0

1

0

y

Q2 Q3 Q4

x Q1

000

001

011

010

110

111

101

100

00

-

0

0

0

1

1

1

0

01

0

1

-

1

-

-

-

1

11

1

-

0

1

-

-

-

-

10

-

0

0

0

1

1

1

0

Таким образом, получена система булевых функций:

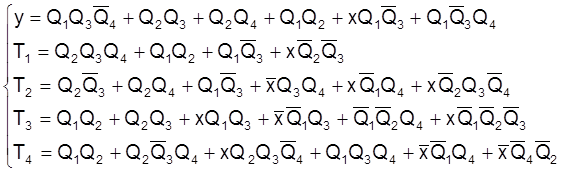
4.3. Совместная минимизация

Просматривая в найденной системе булевых функций каждое уравнение, находим и выделяем общие части – коньюктивные термы zn, которые будем использовать для упрощения функций и самой схемы, реализующей эти функции.

Совместная минимизация дает следующую систему булевых функций:


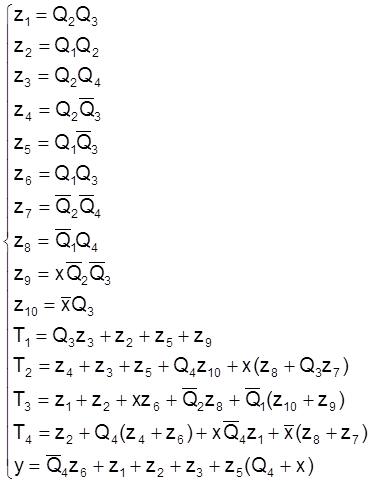
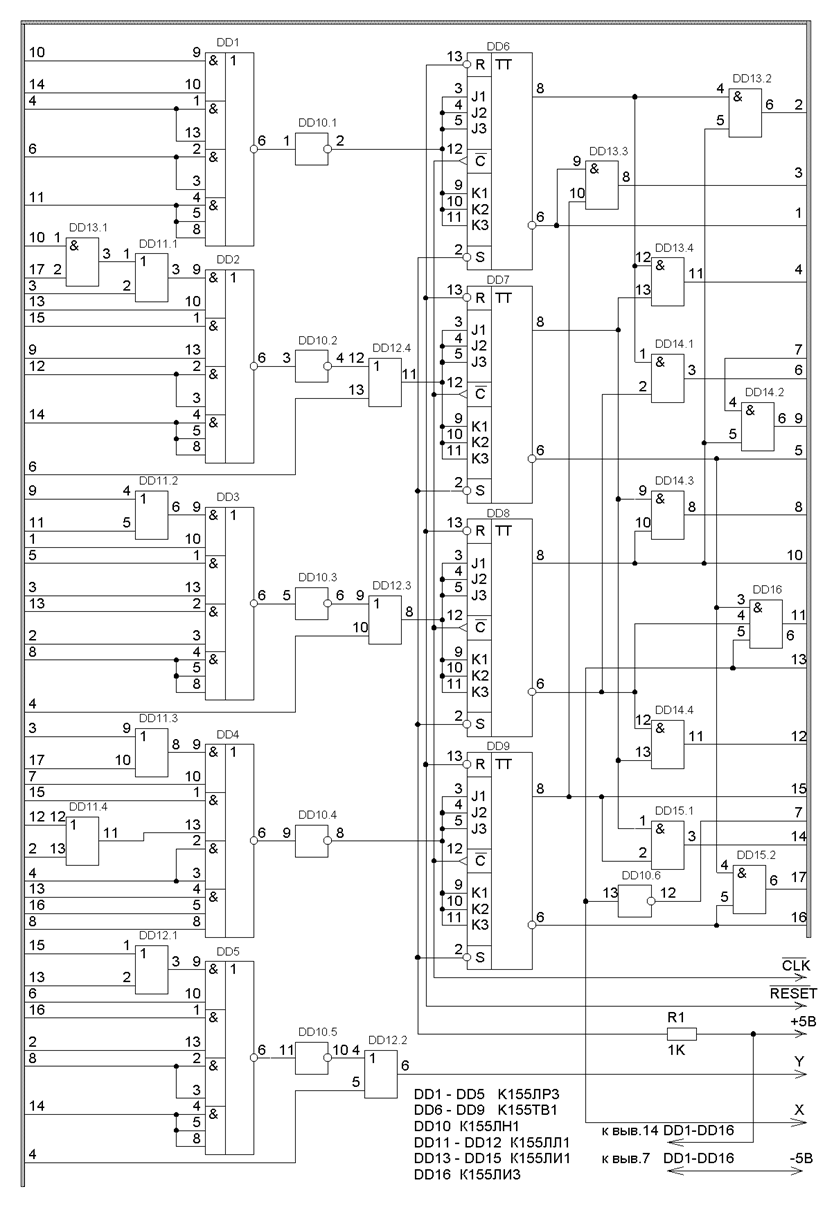
4.4. Реализация на элементах малой степени интеграции (микросхемы серии К155)

4.5. Реализация с использованием элементов средней степени интеграции (дешифратор К155).

Таблица значений кода на выходах дешифраторов:

Входы

Значения кода на шине выходов дешифраторов

x

Q1

Q2

Q3

Q4

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

0

0

0

0

0

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

0

0

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

0

1

0

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

0

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

1

0

0

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

1

0

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

1

1

0

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

0

0

0

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

0

0

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

0

1

0

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

0

0

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

0

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

0

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

0

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

0

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

0

0

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

0

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

0

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

0

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

В соответствии с этой таблицей, а также с таблицой построения булевых функций для T-триггера получаем функции выходов комбинационной схемы:

В данной системе числа являются идентификаторами проводников в шине

Похожие материалы

Информация о работе

ВУЗ:
Нижегородский государственный технический университет им. Р. Е. Алексеева (НГТУ им. Алексеева)
Предмет:
Теория автоматов
Тип:
Курсовые работы
Категория:
Информатика и выч. техника (Технические предметы)
Размер файла:
4 Mb
Скачали:
0
Скачать файл