8 КЛЮЧЕВЫЕ непосредственные СТАБИЛИЗАТОРЫ
8.1 ФОРМА И ПАРАМЕТРЫ НАПРЯЖЕНИЙ, ОБРАЗУЮЩИХСЯ ПРИ РАБОТЕ КЛЮЧА
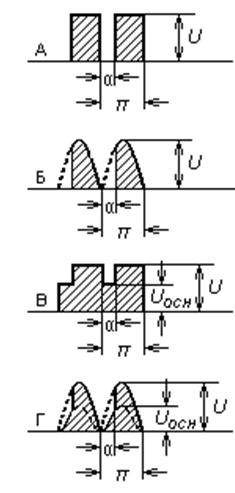
Напряжения, образующиеся при работе ключа, обычно имеют одну из четырёх форм, представленных на рис.8.1.
Для характеристики кривой представляют интерес следующие её параметры :
|
Рисунок 8.1 Кривые напряжений, обр. при работе ключа А-Б без вольтдобавочного устройства В-Г с вольтдобавочным устройством |
1)
относительная величина среднего значения напряжения ![]()
2) относительная величина эффективного значения напряжения
![]()
3) коэффициент формы ![]()
4) относительная величина пульсаций
![]()
где U,Uср,Uэф - соответственно амплитудное, среднее и эффективное значения напряжения, U1- амплитуда первой гармоники кривой напряжения.
Если для стабилизаторов c вольтодобавочным устройством обозначить
![]()
где Uосн-
амплитуда напряжения основного нерегулируемого выпрямителя (кривые В и Г),то
можно сказать, что кривые А и Б являются частными случаями кривых В и Г при ![]() .Поэтому, найдя выражения
для указанных выше параметров, соответствующие кривым В и Г , и подставив в них
.Поэтому, найдя выражения
для указанных выше параметров, соответствующие кривым В и Г , и подставив в них
![]() , получим выражения
для тех же параметров, но относящиеся к кривым А и Б.
, получим выражения
для тех же параметров, но относящиеся к кривым А и Б.
Рассмотрим отдельно перечисленные выше параметры.
Относительная величина среднего значения напряжения. Исходя из общего уравнения , определяющего среднее значение периодической функции
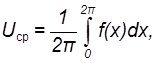
находим для кривых рис. 8.1.
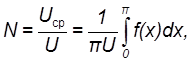
откуда
получаем выражение для параметра N , соответствующее кривой В:![]()
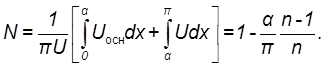 (8.1)
(8.1)
Аналогично для кривой Г:
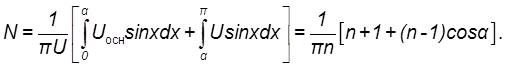 (8.2)
(8.2)
Подставив
в полученные формулы ![]() ,
находим соответственно для кривой А:
,
находим соответственно для кривой А:
![]() (8.3)
(8.3)
и для кривой Б:
![]() (8.4)
(8.4)
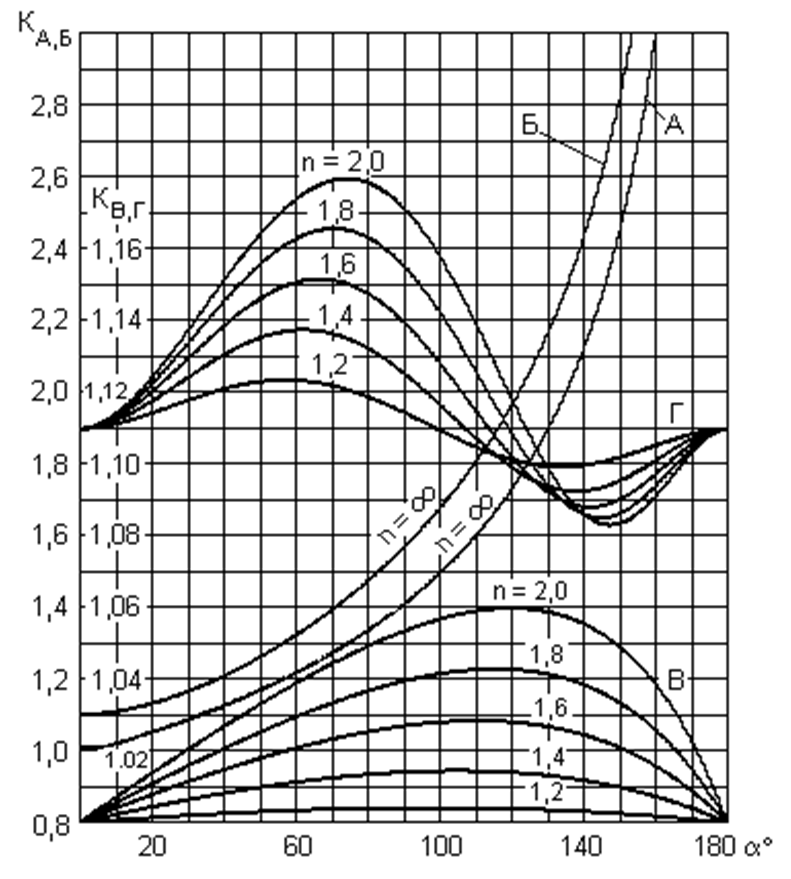
Графики , построенные по уравнениям (8.1)-(8.4) , представлены на рис. 8.2.
Относительная величина эффективного значения напряжения. Из общего выражения для эффективного значения периодической функции
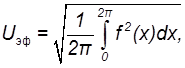
получаем
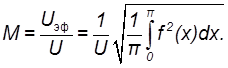
Подставив в это выражение значение f(x) , соответствующее кривой В , находим
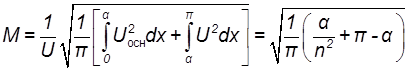 (8.5)
(8.5)
и для кривой Г
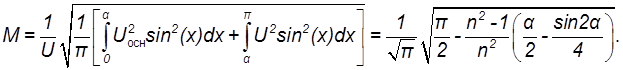 (8.6)
(8.6)
Подставляя
![]() , получаем для кривой
А
, получаем для кривой
А
![]() (8.7)
(8.7)
и для кривой Б
![]() (8.8)
(8.8)
Кривые , построенные по уравнениям (8.5)-(8.8) , приведены на рис. 2.3.
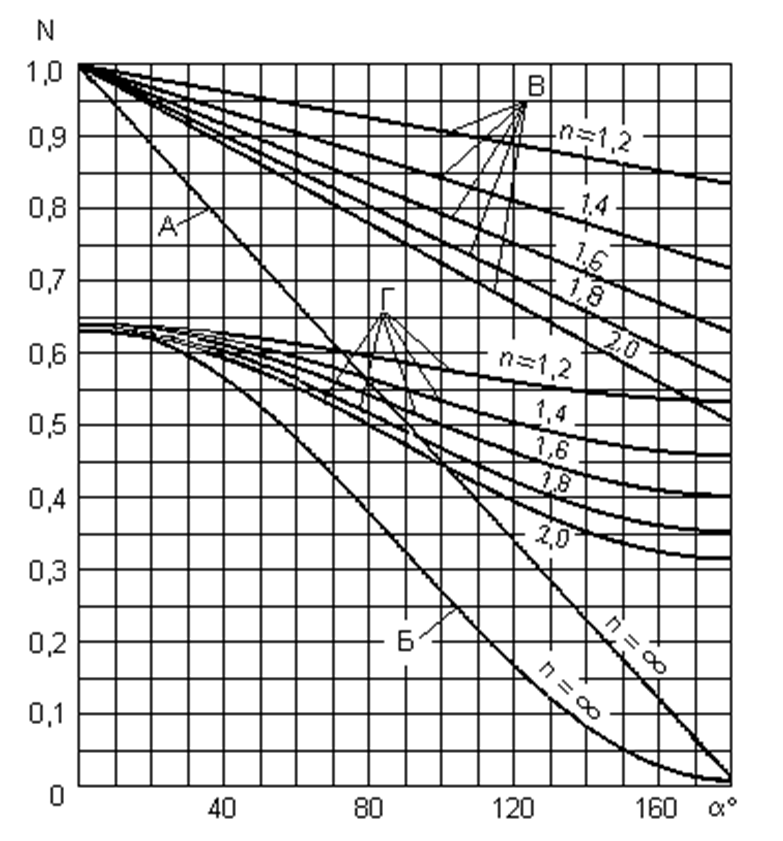
Рисунок 8.2 Зависимость N=f(a)
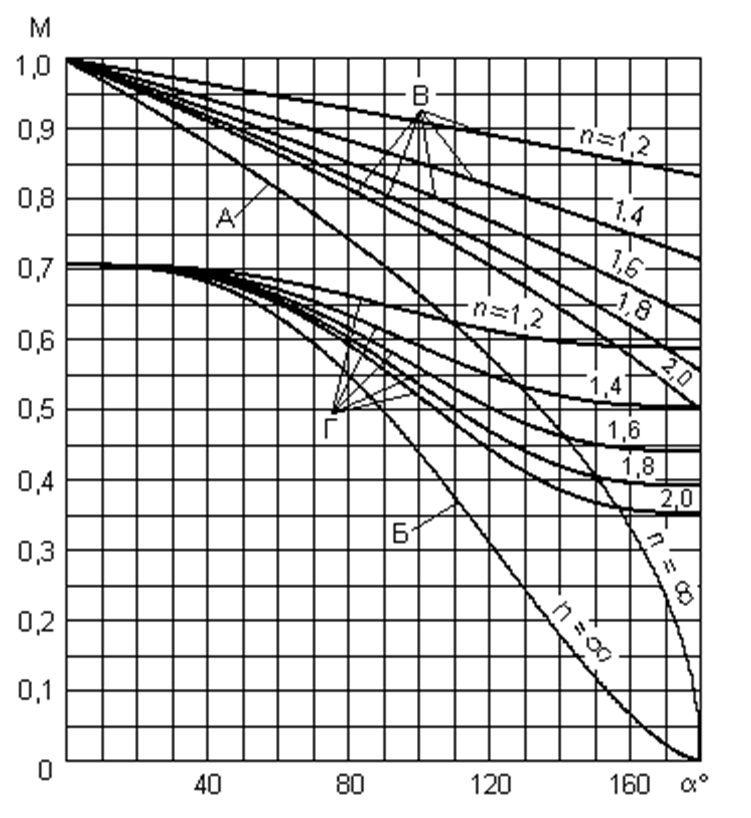
Коэффициент формы.
Полученные выражения для параметров N и M позволяют легко определить коэффициент формы
![]()
Следовательно, для кривой А
![]() (8.9)
(8.9)
для кривой Б
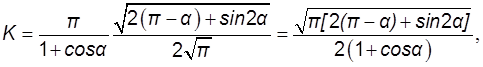 (8.10) для кривой В
(8.10) для кривой В
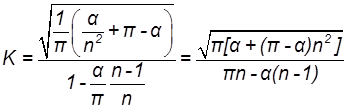 (8.11)
(8.11)
и для кривой Г
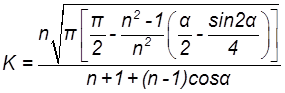 .
(8.12)
.
(8.12)
Кривые , соответствующие уравнениям (8.9)-(8.12) , приведены на рис. 8.4.
Относительная величина пульсаций.
Относительную величину пульсаций найдём, исходя из выражения
![]()
где амплитуда первой гармоники
напряжения ![]()
![]() и
и ![]() - коэффициенты
- коэффициенты
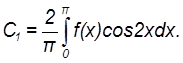 |
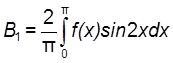 |
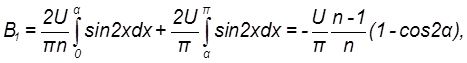
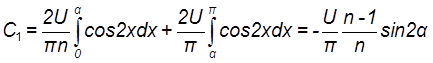
и с учётом уравнения (8.1)
![]() .
(8.13)
.
(8.13)
Аналогично для кривой Г:
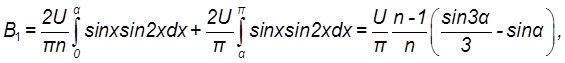
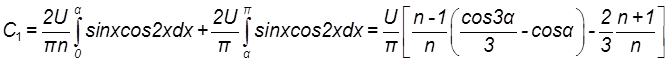
и с учётом уравнения (8.2)
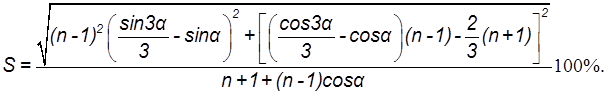 (8.14)
(8.14)
Подставляя в уравнения (8.13)
и (8.14) ![]() , получаем для кривой А
, получаем для кривой А
![]() (8.15)
(8.15)
и для кривой Б
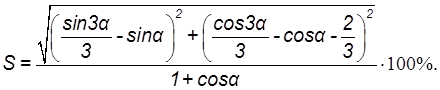 (8.16)
(8.16)
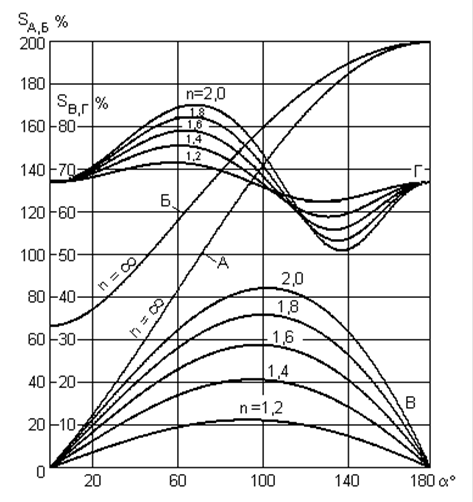 Полученные выражения для
относительной величины пульсаций представлены в виде графиков на рис. 8.5.
Полученные выражения для
относительной величины пульсаций представлены в виде графиков на рис. 8.5.
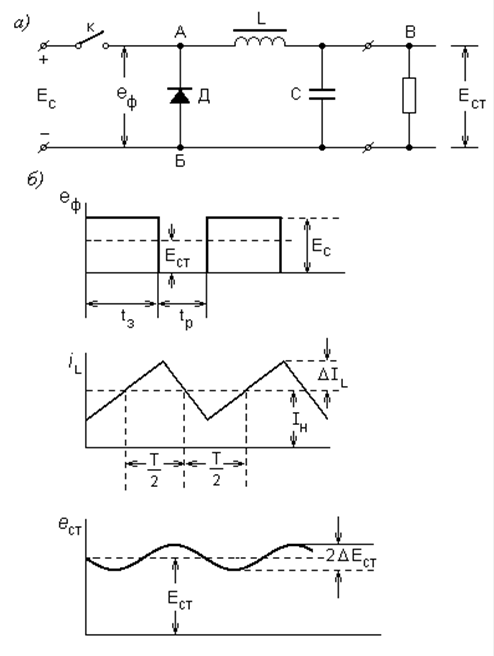 8.2 Сглаживающий фильтр
8.2 Сглаживающий фильтр
Рисунок 8.6 Сглаживающий фильтра) схемаб) диаграммы токов и напряжений. |
Для сглаживания пульсаций , образующихся в стабилизаторе при работе ключа , обычно применяется LC-фильтр (рис. 8.6а) , на входе которого установлен диод Д. При замкнутом ключе К диод находится под обратным напряжением и не оказывает влияния на работу схемы. В э то время происходит накопление энергии в дросселе и конденсаторе фильтра. При размыкании ключа ток продолжает протекать через нагрузку за счёт энергии, накопленной в элементах фильтра. Диод Д замыкает цепь тока, протекающего через дроссель. Зная форму кривой напряжения, образующегося после ключа (см.рис. 8.5),можно найти величину амплитуды первой гармоники и затем рассчитать фильтр по общеизвестной формуле
![]() (8.17)
(8.17)
где q
– заданный коэффициент сглаживания ; ![]() - круговая частота
первой гармоники пульсаций.
- круговая частота
первой гармоники пульсаций.
В ряде схем ключевых стабилизаторов (особенно релейных) фильтр оказывает влияние на работу всего устройства. Поэтому остановимся несколько более подробно на физических процессах, происходящих в нём. Рассмотрим наиболее часто встречающийся случай работы фильтра при сглаживании прямоугольных импульсов
напряжения.
Предположим
для упрощения расчёта , что величина тока нагрузки ![]() в
течение периода работы ключа остаётся постоянной. Учитывая сравнительно малую величину
пульсаций , такое допущение вполне оправдано. Из схемы рис. 8.6а следует, что
напряжение на дросселе будет равно (пренебрегая
в
течение периода работы ключа остаётся постоянной. Учитывая сравнительно малую величину
пульсаций , такое допущение вполне оправдано. Из схемы рис. 8.6а следует, что
напряжение на дросселе будет равно (пренебрегая
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.