Метод Монте-Карло. Применение метода Монте-Карло при анализе привлекательности инвестиционного проекта

предыдущей статье 1 я уже останавливался на разделении ответственности между различными менеджерами в связи с риск-менеджментом.

Возьмем, к примеру, планирование продаж, управление запасами (закупками) и ассортиментную политику. Это прямая задача коммерческого директора, но без использования ряда финансовых процедур и процедур из арсенала риск-менеджмента этот процесс будет носить половинчатый и непоследовательный характер. Вроде бы все ясно с этим вопросом – теория управления запасами хорошо проработана. Даже для вероятностных моделей существуют формулы определения оптимального заказа с учетом платы за дефицит, и, казалось бы, зачем для этой области применять сложные модели из области риск-менеджмента? Рискну заметить, что, на мой взгляд, все эти формулы в реальной жизни не применимы, а если и применимы, то не дают реального оптимального решения в связи с большим количеством стохастических переменных, которые трудно, а порой и невозможно учесть в аналитических решениях. В этом случае (то есть в любой практической задаче) на помощь приходит метод Монте-Карло.

Рассмотрим предельно простую задачу: у нас есть на складе определенное количество товара (например, легковые автомобили), срок исполнения заказа носит вероятностный характер, спрос носит также вероятностный характер (среднее значение и дисперсия стохастических величин нам известны). Вопрос: какое количество товара нам надо заказать? Можно взять средние значения входных данных и применить аналитические формулы. Но давайте теперь промоделируем эту ситуацию и найдем некий коэффициент k, который покажет отличие аналитического решения от решения, полученного методом Монте-Карло. Для начала необходимо выбрать переменную, которое оказывает наибольшее влияние на решение. Такой переменной, скорее всего, является стоимость капитала R. Ведь в условиях вероятностного спроса, чтобы не допустить возникновение дефицита, необходимо заказывать товара чуть больше, но стоимость хранения излишков товара в первую очередь связана со стоимостью капитала. Таким образом, решение выглядит следующим образом: закажешь много – часть прибыли съест финансирование излишков, закажешь мало – недополучишь часть прибыли вследствие дефицита. Скорее всего, существует оптимум. Это типичная оптимизационная задача, с подобными которой менеджер встречается на каждом шагу.

Построив простую модель в Excel’е для некоторых значений и изменяя стоимость капитала, проведем 10 000 испытаний для каждого значения R и k. Результат моделирования для вероятностного спроса с коэффициентом вариации, равным 0,2, представлен на рисунке:

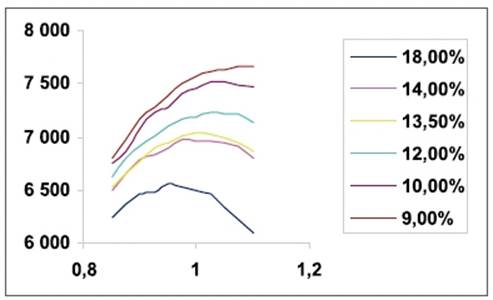
Как видно из графика, действительно имеется некоторое оптимальное решение. Проведем расчет для 3 вариантов вероятностного спроса, вариации которых равны 0,4; 0,3; 0,2, и построим кривые коэффициента k, приводящего к оптимальному решению для разных коэффициентов вариации:

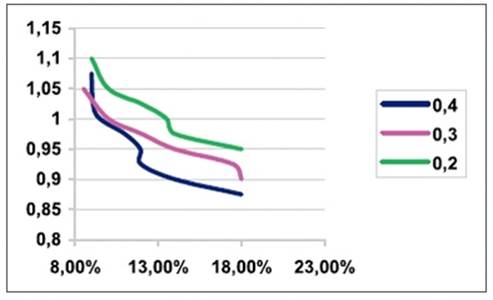
Из графика видно, что k равно 1 только для низких значений стоимости капитала. Метод Монте-Карло также позволяет определить вероятностные характеристики полученных решений – волатильность (или вариацию) и Value at Risk (вероятность получения убытков (ВУ)).

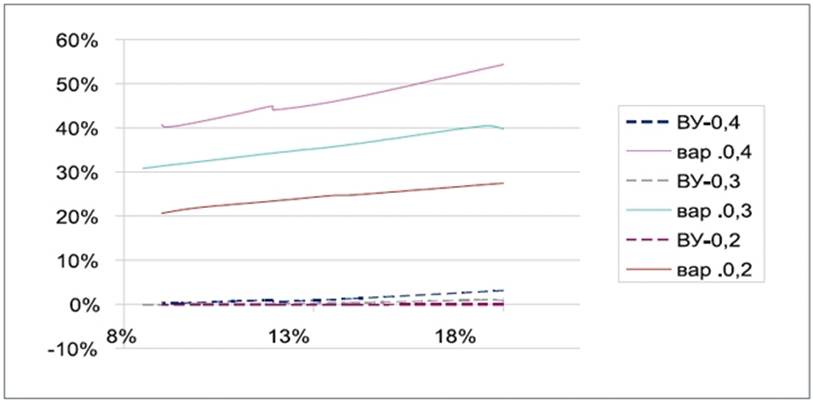
Как можно заметить, волатильность решения возрастает с ростом стоимости капитала, также возрастает и вероятность убытков.

Метод Монте-Карло в отличие от аналитических методов позволяет работать с входными данными со сложной структурой. Например, стоимость капитала редко бывает для компании постоянной величиной. Обычно она зависит от объема инвестиций, так как у нас существуют разные источники привлечения капитала с разными стоимостями, а кроме того, с увеличением долговой нагрузки может изменяться и ставка. Только метод Монте-Карло поможет в случае с нелинейными или логическими переменными.

Метод Монте-Карло незаменим, если нам требуется не просто определить конкретное значение переменной, но нужно найти некий алгоритм, приводящий к оптимизации. В этом случае аналитические методы совсем не применимы. Правда, определение этих алгоритмов все равно лежит на совести менеджмента. Метод Монте-Карло находит практическое применение в таких областях менеджмента, где, казалось бы, безраздельно царят методы линейного программирования, например транспортные задачи.

Если критерием мы выберем не прибыль, а капитализацию, то волатильность скажется на стоимости собственного капитала. Необходимо очень осторожно подходить к этому вопросу. При выборе, к примеру, в качестве критерия показателя EBITDA