Оптимизация финансовых ресурсов предприятий, перерабатывающих сырье

Оптимизация финансовых ресурсов предприятий, перерабатывающих сырье

Аннотация. В статье исследуются вопросы эффективного использования ресурсов предприятия для переработки строго ограниченного количества сырья. Для этого применяется разработанная автором математическая модель, позволяющая на практике получать заранее заданные финансовые результаты. Делаются соответствующие выводы прикладного характера.

Abstract. In the paper the problems of the effective use of the plant resources for processing of the restricted amount of raw have been researched. For this purpose the author's mathematical model has been used allowing to obtain the specified beforehand financial results. The applicable conclusions have been made.

1. Введение

Для перерабатывающих предприятий основным вопросом выживаемости являются своевременные и стабильные поставки сырья. Но в условиях экономической нестабильности и хаоса многие частные компании направляют сырьевые потоки в основном на экспорт, создавая тем самым их дефицит внутри страны. Перерабатывающие предприятия испытывают нехватку сырья для нормальной загрузки имеющихся производственных мощностей. В этой ситуации для повышения эффективности использования трудовых ресурсов и получения прибыли необходимо выработать оптимальную производственную программу выпуска продукции. Если предприятие имеет возможность из одного наименования сырья получать несколько видов продукции, то этим следует воспользоваться и составить программный перечень оптимального ассортимента выпускаемой продукции. И лишь после этого составляется математическая модель максимизации объема производства с учетом ограничений на сырье и численности рабочих.

2. Математическая модель

Перерабатывающее предприятие испытывает острую нехватку сырья для обработки и производства нескольких видов продукции. При ограниченных возможностях в получении достаточного количества сырья от поставщика ставится задача эффективного использования имеющегося в наличии сырья и возможных его поставок в дальнейшем. При этом необходимо получить удовлетворительные показатели финансовых результатов работы перерабатывающего предприятия (Чернов, 1996). Основным среди них является показатель прибыли, играющий важную роль в создании финансовой базы предприятия. За счет прибыли осуществляются мероприятия по расширенному воспроизводству, самофинансированию и материальному стимулированию трудового коллектива. Получаемая прибыль также характеризует степень деловой активности и конечный финансовый результат работы предприятия. Но исходным моментом в получении прибыли является положительный результат от производства и реализации продукции. Только после реализации продукции наступает возможность предприятия своевременно рассчитаться с поставщиками сырья и покрыть все авансированные на производство продукции расходы. Поэтому в модели максимизируется показатель товарной продукции, а на прибыль накладывается ограничение получения ее не ниже определенного уровня (Чернов, 1995).

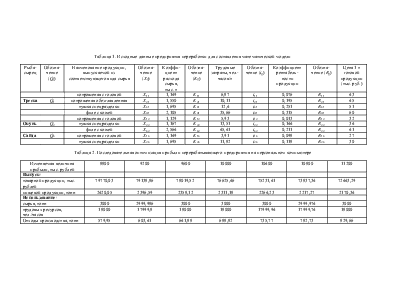
Построение математической модели необходимо начинать с идентификации переменных. Пусть:

R_ij - коэффициент рентабельности продаж i-ой продукции, вырабатываемой из j-го вида сырья;

Kij - коэффициент расхода j-го вида сырья для выпуска i-го названия продукции;

Pij - цена i-ой продукции, вырабатываемой из j-го вида сырья;

t_ij - количество человеко-часов, затрачиваемое на выпуск i-ой продукции, вырабатываемой из j-го вида сырья;

n_j - количество наименований продукции, получаемой из j-го вида сырья;

Q_j - количественный объем j-го вида сырья;

П - минимальный уровень прибыли, необходимый для нормального финансового состояния предприятия;

Т - ограничения по трудовым ресурсам.

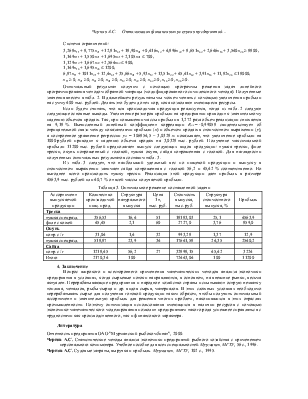
Следующий шаг состоит в том, чтобы сформировать ограничения. Запишем первое ограничение по сырью в виде нескольких неравенств: