Решение матричных игр в смешанных стратегиях. Основы теории принятия решений

Решение матричных игр в смешанных стратегиях.

Исследование в матричных играх начинается с нахождения её седловой точки в чистых стратегиях. Если матричная игра имеет седловую точку в чистых стратегиях, то нахождением этой седловой точки заканчивается исследование игры. Если же в игре нет седловой точки в чистых стратегиях, то можно найти нижнюю и верхнюю чистые цены этой игры, которые указывают, что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры. Улучшение решений матричных игр следует искать в использовании секретности применения чистых стратегий и возможности многократного повторения игр в виде партии. Этот результат достигается путём применения чистых стратегий случайно, с определённой вероятностью.

Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.

Таким образом, если игрок 1 имеет  m  чистых стратегий  1,2,...,m, то его смешанная стратегия  x – это набор чисел  x = (x₁, ..., x_m) удовлетворяющих соотношениям

x_i ³ 0  (i = 1,m),    = 1.

Аналогично для игрока 2, который имеет  n  чистых стратегий, смешанная стратегия  y – это набор чисел

y = (y₁, ..., y_n),  y_j ³ 0,  (j = 1,n), 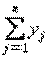 = 1.

Так как каждый раз применение игроком одной чистой стратегии исключает применение другой, то чистые стратегии являются несовместными событиями. Кроме того, они являются единственными возможными событиями.

Чистая стратегия есть частный случай смешанной стратегии. Действительно, если в смешанной стратегии какая-либо i-я  чистая стратегия применяется с вероятностью 1, то все остальные чистые стратегии не применяются. И эта  i-я  чистая стратегия является частным случаем смешанной стратегии. Для соблюдения секретности каждый игрок применяет свои стратегии независимо от выбора другого игрока.

Определение. Средний выигрыш игрока 1 в матричной игре с матрицей А выражается в виде математического ожидания его выигрышей

E (A, x, y) = 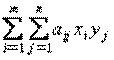= x A y^T

  Первый игрок имеет целью за счёт изменения своих смешанных стратегий  х  максимально увеличить свой средний выигрыш Е (А, х, y), а второй – за счёт своих смешанных стратегий стремится сделать Е (А, х, y) минимальным, т.е. для решения игры необходимо найти такие  х  и  y, при которых достигается верхняя цена игры

 Е (А, х, y).

Аналогичной должна быть ситуация и для игрока 2, т.е. нижняя цена игры должна быть

 Е (А, х, y).

Подобно  играм, имеющим седловые точки  в чистых стратегиях, вводится следующее определение: оптимальными смешанными стратегиями  игроков 1 и 2 называются такие наборы  х^о, у^о  соответственно, которые удовлетворяют равенству

 Е (А, х, y) = Е (А, х, y) = Е (А, х^о, у^о).

Величина  Е (А, х^о ,у^о) называется при этом ценой игры и обозначается через  u.

Имеется и другое определение оптимальных смешанных стратегий:  х^о, у^о называются оптимальными смешанными стратегиями соответственно игроков 1 и 2, если они образуют седловую точку:

Е (А, х, у^о) £ Е (А, х^о, у^о) £ Е (А, х^о, у)

Оптимальные смешанные стратегии и цена игры называются решением матричной игры.

Основная теорема матричных игр имеет вид :

Теорема (о минимаксе). Для матричной игры с любой матрицей А величины

 Е (А, х, y)  и   Е (А, х, y)

существуют и равны между собой.

Теория игр и статистических решений 1. Цели и задачи теории игр и статистических решений. В настоящее время математические методы находят широкое применение в различных областях человеческой деятельности. Помимо строгих математических методов, применяемых для описания различных физических процессов, приходится рассматривать неклассические методы. Дело в том, что не все процессы могут быть описаны строгим математическим языком. При применении классических методов абстрагируется от сущности проблемы, и решают задачи при определенных условиях; при этом часто не учитывают различные факторы, которые могут повлиять на решение задачи. Эти факторы могут быть неизвестными (неопределенными ). Различают два вида неопределенностей. Неопределенности первого вида обусловлены факторами, которые являются предметом изучения в теории вероятностей. Такие факторы представляют собой либо случайные величин, либо случайные функции. Они описываются определенными статистическими характеристиками, которые известны или же могут быть получены. Такого рода неопределенности называют вероятными или, иначе стохастическими. Неопределенности второго вида обусловлены неизвестными факторами, которые нельзя отнести к категории случайных величин (случайных функций ) по той же причине, что набор реализаций этих факторов не обладают статистической устойчивостью и, поэтому не позволяет ввести понятие вероятности. Разумеется, когда речь идет о неопределенности ситуации, выводы