Разработка алгоритмов и программ выполнения операций над последовательными и связанными представлениями структур данных

Принцип решения основан на методе полного перебора, что конечно не лучший вариант, но все-таки лучше, чем ничего.

Аномалии исходных данных и реакция программы на них:

1.  нехватка памяти при распределение: вывод сообщения на экран и завершение работы программы;

2.  неверный формат файла: вывод сообщения на экран и завершение работы программы;

Входные данные

Входными данными для моей работы является начальное число вершин графа, которое по мере работы программы увеличиться на 30 верши. Это число не может превосходить значения 80 вершин, так как в процессе работы программы число увеличивается на 30 и становиться 110 – это «критическое» число получается из расчета 110»2¹⁶/3. Это происходит потому, что стандартный тип int не может вместить в себя более чем 2¹⁶. Мне же требуется для нормально работы программы, чтобы тип вмещал в себя утроенное количество вершин неориентированного графа. Конечно, это всего лишь приближение, но с учётом того, что графы генерируются случайно возможность набора 33000 невелико и, следовательно, допустимо.

Входной файл генерируется каждый раз новый.

Графы для расчета мультипликативных констант генерируются случайным образом, используя датчик случайных чисел, это-то и накладывает ограничения на количество вершин. Дело в том, что при работе с генератором случайных чисел предпостительно иоспользовать целый тип данных – так говорил товарищ Подбельский В.В.

Оценка временной сложности.

Каткие сведения о временной сложности.

            Качество алгоритма оценивается как точность решения и эффективность алгоритма, которая определяется тем временем, которое затрачивается для решения задачи и необходимым объёмом памяти машины.

            Временная сложность алгоритма есть зависимость от количества выполняемых элементарных операций как функция размерности задачи. Временная сложность алгоритма А обозначается .

            Размерность задачи – это совокупность параметров, определяющих меру исходных данных. Временная оценка алгоритма бывает двух типов:

1.  априорная – асимптотическая оценка сложности

2.  апосториорная – оценка сложности алгоритма с точностью до мультипликативных констант, сделанных для конкретной машины.

Именно асимптотическая оценка алгоритма определяет в итоге размерность  задачи, которую можно решить с помощью ЭВМ. Если алгоритм обрабатывает входные данные размера Nза время CN², где С – некая постоянная, то говорят, что временная сложность этого алгоритма есть . Вернее говорить, что положительная и нулевая функция  есть , если существует такая постоянная С, что  для всех отрицательных значений N.

Вычисление временной сложности.

            Для того, чтобы проверить правильность временной оценки алгоритма, надо знать априорную оценку сложности.

            Проверка вычислительной сложности алгоритма сводиться к экспериментальному сравнению двух или более алгоритмов, решающих одну и ту же задачу. При этом возникают две главные проблемы: выбор входных данных и перевода результатов эксперимента в графики кривых сложности.

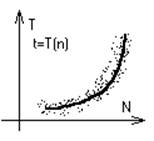
            При прогоне программы мы получаем значения функции, которые можно изобразить на графике как функцию f(NX,NY,NZ). Данные точки показывают характер кривой. Для аппроксимации этого облака точек в своей курсовой работе я использовал метод наименьших квадратов.

            Анализ по методу наименьших квадратов заключается в определении параметров кривой, описывающих связь между некоторым числом Nпар значений Xi, Yi (в данном случае n и tсоответственно), обеспечивая при этом наименьшую среднеквадратичную погрешность. Графически эту задачу можно представить следующим образом – в облаке точек Xi, Yiплоскости XY (смотри  рисунок) требуется провести прямую так, чтобы величина всех отклонений отвечала условию:

        N

F = 

K=1

Где

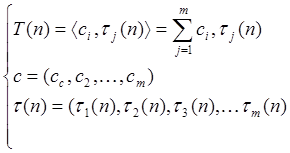
В моём случае T(NX,NY,NZ)=O(NX*(NY+NZ) =>

T(NX,NY,NZ)=C1*NX*(NY+NZ)+C2*(NY+NZ)+C3*(NY)+C4*(NZ)

Следовательно для моего примера мы получим:

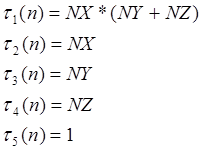
Для того чтобы получить значение функции на K-том эксперименте, мы засекаем значение времени перед вызовом функции, которая реализует алгоритм, вставим оператор вида:

TikTak=clock();

Где функция clock() даёт время с точностью до нескольких миллисекунд (в языке С++ она описана в заголовочном файле time.h). После выполнения процедуры, реализует алгоритм, мы находим разность времени

TikTak=cloc() - TikTak;

После всех проделанных манипуляций нужно прировнять к нулю все частные производные. Это будет выглядеть, в общем виде, примерно так:

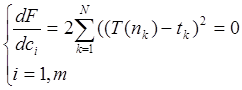
После раскрытия скобок и замены T(n)=T(n)=(c,t(n))= 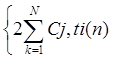получим

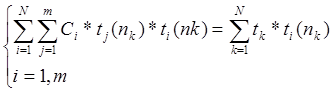
Положим Аij=(ti, tj) и B=(ti,TikTak) => мы получили систему уравнений AX=B, где Х=С. Формирование в матрице столбцов А и столбцов В записывается очень