Статистические свойства МНК оценок параметров регрессии. Доверительный интервал

Необходимость в подборе эмпирических формул возникает во многих случаях. Так, если аналитическое выражения сложное, требует громоздких вычислений, составления программ для ЭВМ или вообще не имеет аналитического выражения, то эффективнее пользоваться упрощённой приближённой эмпирической формулой.

Эмпирические формулы должны быть по возможности наиболее простыми и точно соответствовать экспериментальным данным в пределах изменения аргумента. Таким образом, эмпирические формулы являются приближёнными выражениями аналитических формул. Замену точных аналитических выражений приближёнными, более простыми называют аппроксимацией, а функции – аппроксимирующими.

Методы подбора эмпирических формул

Обычно экспериментальные точки на графике имеют случайные отклонения от видимой общей закономерности. Эти отклонения связаны с неизбежными при всяком опыте погрешностями. Желательно обработать экспериментальные данные так, чтобы по возможности точно отобразить общую тенденцию зависимости y от x и разработать регрессионную математическую модель. Общепринятым при решении подобных задач является метод наименьших квадратов (МНК), разработанный К. Гауссом (1809г.) и А. Марковым (1900г.). Физический смысл данного метода заключается в том, что требование наилучшего согласования теоретической (выравнивающей, сглаживающей, аппроксимирующей) кривой и экспериментальных точек сводится к тому, чтобы сумма (S)  квадратов экспериментальных точек от теоретической кривой была минимальной.

Разностные модели на примере модели 2-го порядка

(3) 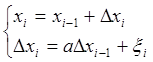        - разностная модель 2-го порядка

 - приращение, характеризует скорость изменения процесса

                                        Модель с приращением удобна в том

                         плане, что не требуется заранее

                          знать коэффициенты регрессии.

Разностные модели 3-го порядка

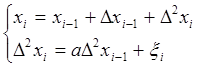
  - 1-я разность

  - 2-я разность

1-я разность характеризует скорость изменения случайного процесса.

2-я разность характеризует ускорение.

Эти модели очень широко иcпользуется на практике, т.к. здесь почти нет коэффициентов, которые нужно идентифицировать ( а и  ), они легко подбираются на ЭВМ по методу наименьших квадратов. Для этого надо иметь реальный процесс отсчетов , модель (4) и нужно воспользоваться следующей формулой МНК/метод наименьших квадратов/

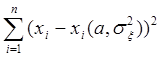         min      где,  - модель,    

 - реальный процесс

Суть МНК состоит в следующем :

Есть  m-отсчетов реального процесса, есть m-отсчетов  модели, составляется сумма квадратов и подбираются параметры (а,) так, чтобы минимизировать эту сумму (делается это на ЭВМ)(метод перебора) но в авторегрессии m-го порядка. Сделать это очень сложно.

Найденные значения коэффициентов а и bаппроксимирующего уравнения y(x) = a + b×x позволяют построить на графике прямую с роящимися вокруг неё точками. Подобным графиком на практике, как правило, завершают регрессионный анализ: график, во-первых, даст наглядное представление о качестве анализа, а во-вторых, поможет в случае чего отловить допущенные ошибки ввода исходных данных (пропуск десятичной точки, например). Этой цели может служить и предварительная сортировка векторов: ошибочные значения часто всплывают на концах упорядоченного вектора.

В-третьих, график сам по себе ценен. Графиком, т.е. с другого конца, можно довольно быстро решить линейную аппроксимационную задачу.

Дополнить результаты регрессионного анализа неплохо указанием точки, максимально отклонившейся от прямой.

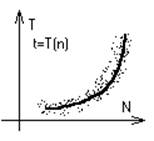
Анализ по методу наименьших квадратов заключается в определении параметров кривой, описывающих связь между некоторым числом Nпар значений Xi, Yi (в данном случае n и tсоответственно), обеспечивая при этом наименьшую среднеквадратичную погрешность. Графически эту задачу можно представить следующим образом – в облаке точек Xi, Yiплоскости XY (смотри  рисунок) требуется провести прямую так, чтобы величина всех отклонений отвечала условию:

        N

F =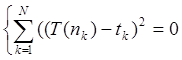 

      K=1

Где

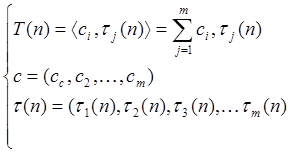
Основной смысл этого метода заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью. (Термин наименьшие квадраты впервые был использован в работе Лежандра - Legendre, 1805.)

2. Доверительный интервал.

Интервал задает пороги принятия и отвержения, которые используются в задачах классификации при решении вопроса о том, относится ли данный выходной набор к конкретному классу. Используются в соответствии с типом функции преобразования выходной переменной (Один-из-N, Два значения, Кохонена и т.д.). Доверительные интервалы для некоторой статистики (например, среднего значения или линии регрессии) показывают диапазон вокруг значения статистики, в котором находится истинное значение этой статистики (с определенным уровнем надежности или доверия).

Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее. Среднее - очень информативная мера "центрального положения" наблюдаемой переменной, особенно если сообщается ее доверительный интервал. Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее. Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия, находится "истинное" (неизвестное) среднее популяции. Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью