Казанское математическое общество
Вводные лекции по курсу
‘‘Высшая математика’’

Г Р А Ф
Казань 1998
УДК 517
ББК 22.16
Ж 66
Вводные лекции по курсу ‘‘Высшая математика’’ /В.Б. ; Казанское математическое общество. Казань, 1998. 46 с.
Пособие написано для широкого круга лиц, изучающих высшую математику и позволяет получить целостное представление об этой дисциплине. Оно может быть использовано преподавателями технических и гуманитарных ВУЗов, а также всеми желающими восстановить знания или самостоятельно начать изучение курса.
Табл. - Ил. - 21 Библ. -
Рецензенты: д.ф.-м.н., проф.
(Казанский государственный университет)
д.ф.-м.н., проф. (НИИММ им.
)
В.Б. , 1998
Глава 1. Пределы
1.1. Предел числовой последовательности
Будем рассматривать множества (совокупности) элементов различной природы, состоящие либо из конечного, либо из бесконечного числа элементов (конечные и бесконечные множества). Множество называется упорядоченным, если для каждых двух его элементов определено, какой из них предшествует другому. Например, координаты (x,y,z) какой–либо точки пространства представляют собой упорядоченное конечное множество (абсцисса x предшествует ординате y, которая в свою очередь предшествует аппликате z).
Элемент множества часто называют точкой множества. Это связано с тем, что, например, между множеством действительных чисел x и точками числовой прямой (так называют прямую, на которой выбраны начало отсчета, масштаб и положительное направление) существует взаимно однозначное соответствие, т. е. каждому действительному числу x соответствует точка на прямой с координатой x, и, наоборот, каждой точке на прямой соответствует определенное действительное число — координата этой точки. Множество точек на прямой (множество действительных чисел) обозначают R1.
Далее, между множеством упорядоченных пар действительных чисел (x,y) и множеством точек на плоскости также существует взаимно однозначное соответствие, т. е. каждой паре чисел (x,y) соответствует точка на плоскости с координатами x, y, и, наоборот, каждой точке плоскости соответствует определенная пара чисел (x,y) — ее координаты. Множество точек на плоскости (множество упорядоченных пар действительных чисел) обозначается R2.
Наконец, существует взаимно однозначное соответствие и между множеством упорядоченных троек действительных чисел (x,y,z) и множеством точек в пространстве, т. е. каждой тройке чисел (x,y,z) соответствует точка в пространстве с координатами x, y, z и, наоборот, каждой точке пространства соответствует тройка чисел (x,y,z) — ее координаты. Множество точек в пространстве (множество упорядоченных троек действительных чисел) обозначают R3.
Обобщая сказанное, можно ввести понятие n-мерного пространства Rn, под которым понимается множество упорядоченных наборов действительных чисел (x1, x2, ... , xn), именуемых точками n-мерного пространства. При этом множество действительных чисел (множество точек прямой) будет одномерным пространством, множество упорядоченных пар действительных чисел (множество точек на плоскости) — двумерным пространством, множество упорядоченных троек действительных чисел (множество точек физического пространства) — трехмерным пространством.
В математике, физике, технике различают величины двух родов: скалярные, характеризующиеся только численным значением (температура, плотность и т. п.), и векторные, характеризующиеся помимо численного значения и направлением (скорость, сила и т. п.). Приняв некоторую точку 0 за изображение нулевого вектора (за начало отсчета), векторную величину геометрически изображают в виде направленного отрезка (вектора) с началом в точке 0, длина которого соответствует численному значению векторной величины, а направление совпадает с направлением векторной величины. Положение вектора на числовой прямой характеризуется одним действительным числом x — координатой его конца; на плоскости — двумя числами (x,y) — проекциями вектора на координатные оси или, что то же, координатами его конца; в физическом пространстве — тремя координатами (x,y,z) — также проекциями вектора на координатные оси или координатами его конца. Соответствие между множеством действительных чисел и векторами на прямой взаимно однозначное, как и между множеством упорядоченных пар действительных чисел (x,y) и векторами на плоскости, или между множеством упорядоченных троек действительных троек (x,y,z) и векторами в физическом пространстве. Поэтому можно рассматривать множество действительных чисел x (пространство R1) не только как множество точек прямой, но и как множество векторов на прямой (с концами в точках с координатой x); множество пар действительных чисел (x,y) (пространство R2) не только как множество точек на плоскости, но и как множество векторов на плоскости с концами в точках с координатами x, y, или с проекциями на координатные оси, равными x, y; множество троек действительных чисел (x,y,z) (пространство R3) не только как множество точек в физическом пространстве, но и как множество векторов в этом пространстве с концами в точках с координатами x, y, z, или с проекциями на координатные оси, равныОмбиоб щx, аyя, zс.к азанное, можно рассматривать множество упорядоченных наборов n действительных чисел x=(x1, x2, ... , xn) (пространство Rn) не только как множество точек n-мерного пространства, но и как множество векторов в этом пространстве (с концами в точках с координатами x1, ... , xn или, что то же, с проекциями на координатные оси, равными x1, ... , xn).
Расстояние между точками x, y на прямой, между точками (x1,y1), (x2,y2) на плоскости и между точками (x1,y1,z1), (x2,y2,z2) в трехмерном пространстве определяется формулами
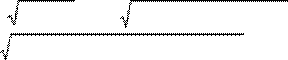 ρ1= | x − y
| = (x − y)2
, ρ2 = (x2 − x1 ) 2+ (y2 − y1)2 ,
ρ1= | x − y
| = (x − y)2
, ρ2 = (x2 − x1 ) 2+ (y2 − y1)2 ,
(1)
ρ3= (x2 − x1)2+(y2 − y1)2+(z2 − z1)2
причем видно, что первые две формулы являются частным случаем третьей. Обобщая формулу (1) на n-мерный случай, определим расстояние между точками x=(x1, ... , xn), y=(y1, ... , yn) n-мерного пространства по формуле
![]() ρn
(x,y)=
(x1
−
y1)2+
L
+(xn
−
yn)2
. (2)
ρn
(x,y)=
(x1
−
y1)2+
L
+(xn
−
yn)2
. (2)
Множество, для элементов которого введено понятие расстояния (введена метрика), называют метрическим пространством. Метрику (2) называют евклидовой метрикой.
Пространство Rn с евклидовой метрикой называют евклидовым
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.