МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
100400 – Электроснабжение
по лабораторной работе № 4
Выполнил:
студент группы 9А03
Принял:
Томск 2003
1. Для заданной цепи определить все токи в переходном режиме (аналитическими методами) и изобразить из графически.
2. Определить токи, напряжения в переходном режиме численными методами. Сравнить полученные результаты и сделать выводы.
3. Определить критерии подобия для данного процесса.
4. Определить будут ли полностью подобны процессы в данной цепи, если во втором процессе уменьшить величину L (или C) в 10 раз, а значение сопротивления R1 увеличить в два раза.
5. Определить значения масштабных коэффициентов и индикаторов подобия для двух рассматриваемых процессов.
Данные расчета:
Таблица 1
|
- |
E, B |
R1, Ом |
L, Гн |
|
iI(t1) |
40 |
10 |
30 |
|
iII(t2) |
40 |
20 |
3 |
Для первого процесса:
|
t, c |
0,33 |
0,5 |
0,67 |
1 |
1,33 |
1,5 |
2 |
2,5 |
|
i1(t1) |
2,102 |
2,148 |
2,191 |
2,264 |
2,325 |
2,354 |
2,424 |
2,478 |
|
i2(t1) |
1,899 |
1,853 |
1,811 |
1,738 |
1,677 |
1,649 |
1,58 |
1,526 |
|
i3(t1) |
0,203 |
0,295 |
0,38 |
0,525 |
0,648 |
0,704 |
0,844 |
0,953 |
Для второго процесса:
|
t, c |
0,01 |
0,015 |
0,02 |
0,025 |
0,03 |
0,035 |
0,04 |
0,045 |
|
i1(t1) |
1,347 |
1,354 |
1,361 |
1,368 |
1,374 |
1,38 |
1,386 |
1,392 |
|
i2(t1) |
1,304 |
1,29 |
1,277 |
1,264 |
1,251 |
1,239 |
1,227 |
1,215 |
|
i3(t1) |
0,043 |
0,064 |
0,084 |
0,104 |
0,123 |
0,141 |
0,159 |
0,177 |
Рис. 1. Схема электрической цепи
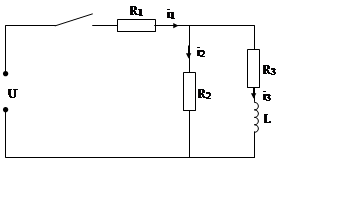
Расчет:
Классический метод (аналитический метод решения дифференциальных уравнений):
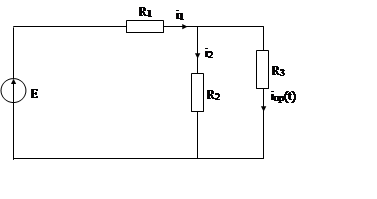
Расчет второго процесса (первый был рассчитан в ИДЗ№3):
ННУ:
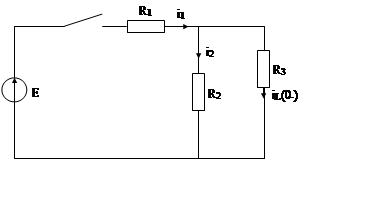
![]()
![]()
ЗНУ:
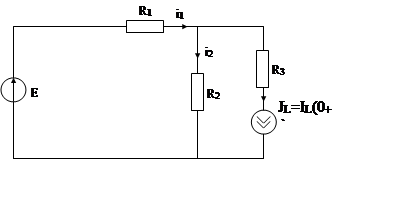
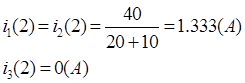
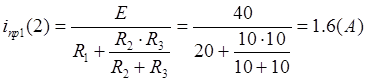
![]()
Корень характеристического уравнения
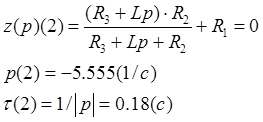
Время затухания переходного процесса
![]()
![]()
Постоянная интегрирования:
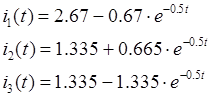
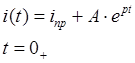
![]() , откуда
, откуда
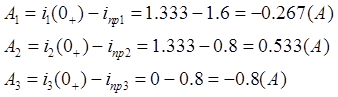
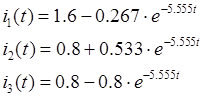
Известно, что процесс в заданной цепи описывается системой уравнений:
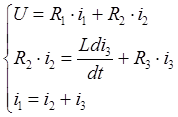
Приведем
исходные уравнения к безразмерному виду, разделив на ![]() ,
I3R3 соответственно:
,
I3R3 соответственно:
Итак:
![]()
![]()
Критерии подобия:
П1=![]() ; П2=
; П2=![]() ; П3=
; П3=![]() ; П4=
; П4=![]() ;
;
Для каждого критерия подобия есть свои степенные комплексы масштабных коэффициентов (индикаторы подобия).
Индикаторы подобия:
I1=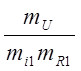 ; I2=
; I2=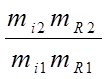 ;
I3=
;
I3=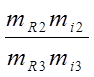 ; I4=
; I4=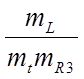 ;
;
Приравняем индикатор подобия I4 к единице и выразим новый масштаб по времени:
I4=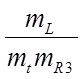 =1;
=1;
mt=mL/ mR3;
mL=30/3=10;
mR3=10/10=1;
mt=10/1=10;
mt=t1/t2 Þ t2=t1/mt =t1/10;
t2=0.02c.
i11=2.064 A; i21=1.367 A;
i12=1.948 A; i22= 1.277 A;
i13= 0.127 A; i23= 0.084 A;
Рассчитаем критерии подобия для процессов 1 и 2:
П11=![]() =
=![]() ; П21=
; П21=![]() ;
;
П12=![]() ; П22=
; П22=![]() ;
;
П13=![]() ; П23=
; П23=![]() ;
;
П14=![]() ; П24=
; П24=![]() ;
;
Вывод:
Критерии подобия П1, П2, П3, П4 можно рассматривать как обобщенные вторичные переменные определенного класса процессов, отражающих специфику группового взаимодействия физических факторов. Этими переменными исследуемые процессы могут быть описаны так же полно, как и первичными размерными физическими факторами. Однако, при переходе критериальному описанию сокращается число переменных, что обеспечивает более высокий уровень универсальности результатов исследования: критериальное описание едино для всех подобных процессов, что позволяет распространить на класс подобных процессов количественные результаты, полученные при исследовании одного из таких процессов.
В ходе выполнения данной лабораторной работы были рассчитаны 2 процесса. Для этих процессов определили критерии подобия, но равенства критериев достичь так и не удалось. Следовательно, процессы не подобны, что можно объяснить некорректно заданными условиями (параметры цепи менялись произвольно).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.