с = с(x,y,z); (2.6)
p = p(x,y,z). (2.7)
Установившееся движение - равномерное, если на данном участке F=const и с = const; примером может служить движение жидкости в цилиндрической трубе при Q = const.
Если при движении жидкости меняются F и с, то движение будет неравномерным.
Неустановившееся движение характеризуется переменными во времени полями скоростей и полями давлений. В этом случае наблюдаются функции:
с = с(x,y,z,t); (2.8)
p = p(x,y,z,t). (2.9)
t - время, с. Примером может служить истечение жидкости из резервуара при переменном уровне.
2.2.1. Уравнение неразрывности
Уравнение будет дано для одномерного потока и установившегося режима. Поток считается одномерным, если параметры изменяются только в направлении движения, по поперечному сечению канала параметры потока остаются постоянными, но по всему соседнему поперечному сечению канала они уже будут другими (все или частично).
Имеем канал (рис. 2.4) с сечениями F1 (параметры в любой точке его скорость с1, удельный объем v1) и F2 (параметры c2, v2), массовый расход жидкости G, кг/с.
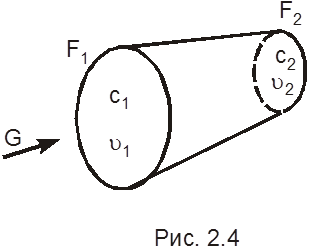
За одну секунду через сечение пройдет, очевидно, объем F1c1 = Q1 = Gv1, откуда G = F1c1/v1; аналогично имеем для второго сечения G = F2c2/v2. Стенки канала непроницаемы, поэтому массовый расход в обоих сечениях один и тот же. Тогда имеем
F1c1/v1 = F2c2/v2 = Fc/v = G = const . (2.10)
Это уравнение справедливо и для газов и для жидкостей. Для жидкостей можно принять v1 = v2: считаем жидкость несжимаемой. Отсюда
c1/c2 = F2/F1 , (2.11)
т.е. средние скорости жидкости в поперечных сечениях потока при неразрывном движении обратно пропорциональны площади этих сечений.
2.2.2. Уравнение Бернулли
Это уравнение справедливо для движущихся жидкостей, а также для газов при их движении со скоростями, много меньшими скоростей распространения в них звука. Оно может быть получено из уравнения 1-го закона термодинамики для потока (уравнения сохранения энергии), доказательство не очень строгое:
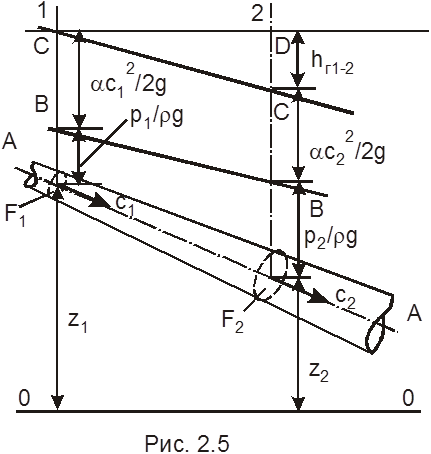
q = h2 – h1 + (c22 - c12)/2 + g(z2 – z1) + lтехн, контрольные сечения канала F1 и F2 даны на рис. 2.5. и и даны необходимые обозначения. Считаем тепло, подводимое извне, q = 0; энтальпия h = u + pv; считаем, что изменение внутренней энергии равно нулю, так как температуру считаем постоянной, u1 = u2; техническую работу приравниваем нулю lтехн = 0; далее v= 1/r, жидкость несжимаема r=const. Тогда
p1/r + c12/2+ gz1 = p2/r + c22 /2+ gz2;
или
p1/(gr )+ c12/(2g)+ z1 = p2/(gr )+ c22 /(2g)+ z2 = Hд=const; (2.12)
это уравнение называется уравнением Бернулли для идеальной несжимаемой жидкости.
Здесь z1, z2 - удельные энергии положения жидкости (геометрические напоры), м; p1/(gr1), p2/(gr2 ) – пьезометрические высоты или энергии давления, м; c12/(2g), c22/(2g) – удельные кинетические энергии в рассматриваемых сечениях, т.е. скоростные напоры, м; Hд – гидродинамический напор.
При течении реальной жидкости необходимо учитывать затраты энергии на преодоление гидравлических сопротивлений hг1-2 на участке между сечениями 1 и 2. В формуле у скоростных напоров необходимо ввести коэффициент учитывающий неравномерность распределения скоростей по площади живого сечения, a = 1,045 ¸ 1,03. Уравнение приобретает вид:
p1 /(gr )+ ac12/(/(2g)+ z1 = p2/(gr )+ ac22 /(2g)+ z2 + hг1-2. (2.13)
Графическое представление уравнения Бернулли для реальной жидкости дано на рис. 2.5.
При наличии между сечениями насоса, создающего напор Hнас, уравнение приобретает вид:
p1/(gr )+ ac12/(/(2g)+ z1 = p2/(gr )+ ac22 /(2g)+ z2 + hг1-2.- Hнас. (2.14)
Гидравлический уклон:
iеидр = (H1 – H2)/l = hг1-2//l, (2.15}
H1 =p1/(gr )+ ac12/(/(2g)+ z1;
H2 = p2/(gr )+ ac22 /(2g)+ z2 ;
l – длина участка, iеидр величина безразмерная.
Пьезометрический уклон:
lp = (p1/(gr ) – p2/(gr ))/l. (2.16)
Геометрический уклон:
lгеом= (z1 – z2)/l . (2.17)
lp, lгеом безразмерны.
Для характеристики режима течения используется критерий Рейнольдса:
Re = сd/n; (2.18)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.