Основы термодинамики. Уравнение состояния идеального газа. Смеси идеальных газов

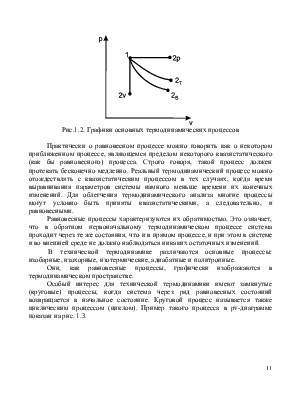
Термодинамический процесс в идеальном случае относится к равновесным, если все параметры системы успевают мгновенно выравниваться, т.е. принимать одни и те же значения по всему ее объему для каждого момента времени. Это происходит за счет протекания в системе различных физических явлений, таких, например, как теплообмен, диффузия и т. д.

Реальные термодинамические процессы часто сопровождаются вредными явлениями, связанными с диссипацией (рассеиванием) энергии системы. Рассеяние энергии происходит, например, за счет трения, вихреобразования и др. Поэтому подобные процессы по своей природе являются неравновесными и протекают при неравновесном взаимодействии внешней среды и системы. Кроме того, возникающие в системе неоднородности значений параметров р, v, T  не успевают выравниваться даже при достаточно больших скоростях этих взаимодействий, что также приводит к неравновесности процесса.

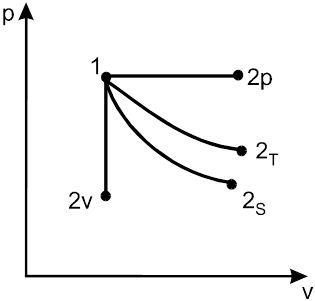Практически о равновесном процессе можно говорить как о некотором приближенном процессе, являющемся пределом некоторого квазистатического (как бы равновесного) процесса. Строго говоря, такой процесс должен протекать бесконечно медленно. Реальный термодинамический процесс можно отождествлять с квазистатическим процессом в тех случаях, когда время выравнивания параметров системы намного меньше времени их конечных изменений. Для облегчениятермодинамического анализа многие процессы могут условно быть приняты квазистатическими, а следовательно, и равновесными.

Равновесные процессы характеризуются их обратимостью. Это означает, что в обратном первоначальному термодинамическом процессе система проходит через те же состояния, чтои в прямом процессе, и при этом в системе и во внешней среде не должно наблюдаться никаких остаточных изменений.

В технической термодинамике различаются основные процессы: изобарные, изохорные, изотермические, адиабатные и политропные.

Они, как равновесные процессы, графически изображаются в термодинамическом пространстве.

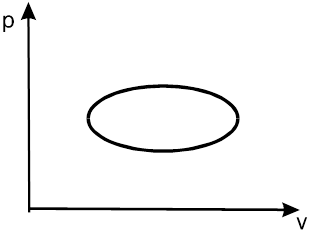
Особый интерес для технической термодинамики имеют замкнутые (круговые) процессы, когда система через ряд равновесных состояний возвращается в начальное состояние. Круговой процесс называется также циклическим процессом (циклом). Пример такого процесса в рv-диаграмме показан на рис. 1.3.

Рис. 1.3. Круговой процесс в рv-диаграмме

1.2.Уравнение состояния идеального газа

Газ, у которого отсутствуют силы взаимодействия между молекулами, а размеры их намного меньше межмолекулярных расстояний, принято называть идеальным газом. В реальных газах нельзя пренебречь силами межмолекулярного взаимодействия и собственным объемом  молекул.

В технике часто приходится иметь дело с реальными газами, близкими по своим свойствам к идеальным газам.

Введение понятия идеальный газ дает возможность связать термические параметры состояния термодинамической системы простой аналитической зависимостью.

В общем виде связь между термическими параметрами однородного вещества р, v и Т в равновесном состоянии имеет вид

j (p, v, T) = 0.

Эта зависимость называется термическим уравнением состояния тела.

Для идеального газа параметры в произвольном состоянии связаны между собой уравнением состояния идеального газа Клапейрона (1834 г.)

pv=RT .                                               (1.1.)

Физическая величина R, Дж/(кг×К), называется газовой постоянной, зависит от природы газа.

Запишем и другие формы уравнения , необходимые для термодинамических расчетов. Умножив на массу газа, получим уравнение состояния идеального газа для m кг: 

pV=mRT.

Здесь V=v×m, м³ – объем газа массой m кг.

При умножении на массу одного к-моля газа m, кг/к-моль, получим уравнение состояния  идеального газа для одного моля:

, где объем 1 кмоля газа при абсолютном давлении р и абсолютной температуре Т , что вытекает из закона Авогадро;  характеризует газовую постоянную для 1 кмоля газа и называется универсальной газовой постоянной, поскольку для всех газов, независимо от их природы, имеет одну и ту же величину. Ее легко вычислить для нормальных значений параметров состояния, а именно

.

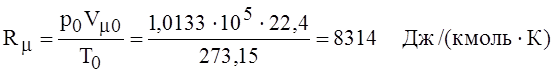Отсюда следует, что газовая постоянная для 1 кг любого конкретного газа может быть сравнительно просто рассчитана по формуле

R=8314/m, Дж/(кг×К).

Молекулярные массы m имеют следующие значения, кг/кмоль: азот – 28, аммиак – 17, аргон – 40, водород – 2, воздух – 29, кислород – 32, окись углерода – 28, углекислый газ – 44.

1.3.Смеси идеальных газов

В инженерной практике чаще приходится иметь дело не с чистыми газами