Кодирование двоичного кода 1001111011111000 с помощью 2B1Q и дифференциального манчестерского кода

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ СПО

НИЖЕГОРОДСКИЙ РАДИОТЕХНИЧЕСКИЙ КОЛЛЕДЖ

КОНТРОЛЬНАЯ РАБОТА

По дисциплине КОМПЬЮТЕРНЫЕ СЕТИ

Выполнил студент

группы 5АС-07-1з

Шифр 18

Вариант 8

Нижний Новгород

2009 год

 Задания

1.  Закодировать двоичный код 1001111011111000 с помощью 2B1Q и дифференциального  манчестерского кода. Улучшить двоичный код с помощью кода 4B/5Q. Заново закодировать код с помощью 2B1Q и дифференциального  манчестерского кода.

2.  Из представленных различных масок, указать маски, которых быть не может.

a)  255.255.255.192

b)  255.255.125.0

c)  255.182.0.0

d)  255.255.8.0

e)  255.255.254.0

f)  255.155.255.128

3.  Из представленных IP-адресов указать адреса, запрещенные для узлов и сетей.

a)  255.255.255.255

b)  167.89.0.0

c)  34.9.21.4

d)  255.23.12.1

e)  192.86.45.11

f)  127.255.255.205

4.  По заданному IP-адресу 206.11.175.39 и маске 255.224.0.0 определить номер сети ( подсети) и номер узла.

5.  Дана сеть класса В: 190.250.0.0. Разделить эту сеть на четыре подсети с N1, N2, N3, N4 компьютерами наиболее экономичным способом (неиспользуемых IP-адресов должно быть как можно меньше), указать пространство IP-адресов каждой подсети и маски подсети. N1=5, N2=256, N3=1000, N4=128.

1.  Закодировать двоичный код 1001111011111000 с помощью 2B1Q и дифференциального  манчестерского кода. Улучшить двоичный код с помощью кода 4B/5Q. Заново закодировать код с помощью 2B1Q и дифференциального  манчестерского кода.

Решение:

Закодируем двоичный код с помощью кода 2B1Q.

Код 2B1Q кодирует следующим образом:

·  комбинация 00 кодируется сигналом – 2,5

·  комбинация 01 кодируется сигналом – 0,833

·  комбинация 10 кодируется сигналом + 2,5

·  комбинация 11 кодируется сигналом + 0,833

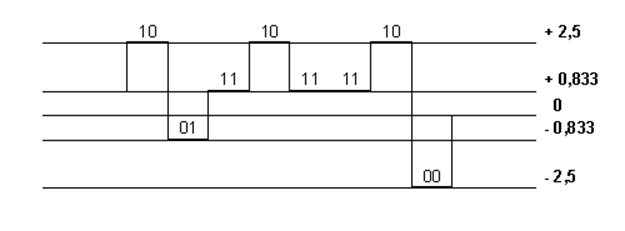
Двоичный код 10 01 11 10 11 11 10 00.

Получаем:

Закодируем двоичный код с помощью дифференциального манчестерского кода.

Дифференциальный манчестерский код кодирует следующим образом:

·  0 кодируется переходом в начале интервала

·  1 кодируется отсутствием перехода в начале интервала

В обоих случаях в середине интервала обязательно присутствует переход.

Двоичный код 1001111011111000.

Получаем:

Улучшим двоичный код с помощью кода 4B/5Q.

4B/5Q кодирует следующим образом:

·  комбинация 0000 кодируется комбинацией 11110

·  комбинация 0001 кодируется комбинацией 01001

·  комбинация 0010 кодируется комбинацией 10100

·  комбинация 0011 кодируется комбинацией 10101

·  комбинация 0100 кодируется комбинацией 01010

·  комбинация 0101 кодируется комбинацией 01011

·  комбинация 0110 кодируется комбинацией 01110

·  комбинация 0111 кодируется комбинацией 01111

·  комбинация 1000 кодируется комбинацией 10010

·  комбинация 1001 кодируется комбинацией 10011

·  комбинация 1010 кодируется комбинацией 10110

·  комбинация 1011 кодируется комбинацией 10111

·  комбинация 1100 кодируется комбинацией 11010

·  комбинация 1101 кодируется комбинацией 11011

·  комбинация 1110 кодируется комбинацией 11100

·  комбинация 1111 кодируется комбинацией11101

Двоичный код 1001 1110 1111 1000.

Получаем 10011 11100 11101 10010.

Закодируем получившийся двоичный код с помощью кода 2B1Q.

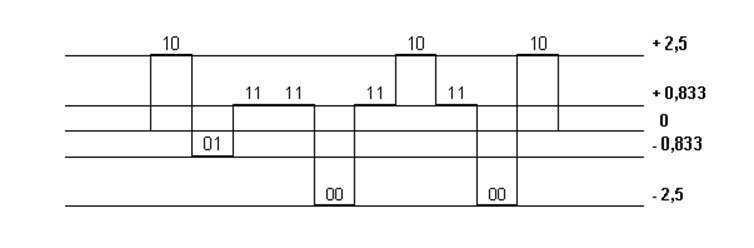
Двоичный код 10 01 11 11 00 11 10 11 00 10.

Получаем:

Закодируем получившийся двоичный код с помощью дифференциального манчестерского кода.

2.  Из представленных различных масок, указать маски, которых быть не может.

3.  255.255.255.192

4.  255.255.125.0

5.  255.182.0.0

6.  255.255.8.0

7.  255.255.254.0

8.  255.155.255.128

Решение:

Переведем маски из десятичного кода в двоичный:

a.  11111111.11111111.11111111.11000000

b.  11111111.11111111.11111101.00000000

c.  11111111.10110110.00000000.00000000

d.  11111111.11111111.00001000.00000000

e.  11111111.11111111.11111110.00000000

f.  11111111.10011011.11111111.10000000

Не может быть масок:

·  11111111.11111111.11111101.00000000

·  11111111.10110110.00000000.00000000

·  11111111.11111111.00001000.00000000

·  11111111.10011011.11111111.10000000

т.к. между единицами в масках не могут стоять нули.

9.  Из представленных IP-адресов указать адреса, запрещенные для узлов и сетей.

a)  255.255.255.255

b)  167.89.0.0

c)  34.9.21.4

d)  255.23.12.1

e)  192.86.45.11

f)  127.255.255.205

Решение:

Адрес 255.255.255.255 – запрещен, т.к. сейчас используются только А, В или С классы сетей (т.е. до адреса 223.255.255.255)

Адрес 167.89.0.0 – разрешен, класс сети В, если маска подсети до 15 единиц (т.е. до 11111111.11111110.00000000.00000000)

Адрес 34.9.21.4 разрешен, класс сети А.

Адрес 255.23.12.1 запрещен, т.к. сейчас используются только А, В или С классы сетей (т.е. до адреса 223.255.255.255)

Адрес 192.86.45.11 разрешен

Адрес 127.255.255.205 разрешен, класс сети А.

10.  По заданному IP-адресу 206.11.175.39 и маске 255.224.0.0 определить номер сети ( подсети) и номер узла.

Решение:

Переведем IP и маску из десятичного кода в двоичный:

IP:               11001110.00001011.10101111.00100111

маска:         11111111.11100000.00000000.00000000

№ сети:       206 (11001110)

№ подсети: 0 (000)

№ узла:       11.175.39 (01011.10101111.00100111)

11.  Дана сеть класса В: 190.250.0.0. Разделить эту сеть на четыре подсети с N1, N2, N3, N4 компьютерами наиболее экономичным способом (неиспользуемых IP-адресов должно быть как можно меньше), указать пространство IP-адресов каждой подсети и маски подсети. N1=5, N2=256, N3=1000, N4=128.

Решение:

От N1=5 (+2) справа 8 (-2=6), от N2=256 (+2) справа 512 (-2=510), от N3=1000 (+2) справа 1024 (-2=1022), от N4=128 (+2) справа 256 (-2=).

Получаем маски подсети:

·  N3=1000:    11111111.11111111.11111100.00000000

·  N2=256:      11111111.11111111.11111110.00000000

·  N4=128:      11111111.11111111.11111111.00000000

·  N1=5:          11111111.11111111.11111111.11111000

Получаем адреса узлов:

·  1000 (1024):         190.250.0.0 – 190.250.3.255 подсеть 0

10111110.11111010.00000000.00000000 – 10111110.11111010.00000011.11111111

·  256 (512):             190.250.4.0 – 190.250.5.255 подсеть 2 (10)

10111110.11111010.00000100.00000000 – 10111110.11111010.00000101.11111111

·  128 (256):             190.250.6.0 – 190.250.6.255 подсеть 6 (110)

10111110.11111010.00000110.00000000 – 10111110.11111010.00000110.11111111

·  5 (8):                     190.250.7.0 – 190.250.7.7 подсеть 224 (11100000)

10111110.11111010.00000111.00000000 – 10111110.11111010.00000111.00000111