Общим решением дифференциального уравнения первого порядка называется функция y = j(x, c), содержащая произвольную постоянную c и удовлетворяющая условиям:
1) функция j(x, c) является решением дифференциального уравнения при любом фиксированном значении с;
2) для любого начального условия y(x0) = y0 найдется такое значение постоянного с = с0, что функция j(x, с0), удовлетворяет этому начальному условию.
Определение 7. Частным решением дифференциального уравнения называется любая функция y = j(x, c0), полученная из общего решения y = j(x, c)
Если общее решение дифференциального уравнения находится в неявном виде F(x, y, c) = 0, то его называют общим интегралом дифференциального уравнения. Уравнение F(x, y, c0) = 0 называют частным интегралом.
Общее решение y = j(x, c) дифференциального уравнения изображается на плоскости в виде семейства интегральных кривых , частное решение y = j(x, c0) - одна кривая этого семейства, проходящая через точку (x0, y0).
Теорема 1 (существования и единственности решения задачи Коши). Пусть дано дифференциальное уравнение
(4)
при начальном условии
y(x0) = y0 (5)
Пусть
далее функция f(x, y) и
ее частная производная
непрерывна
в некоторой области D, содержащей точку
(x0, y0). Тогда существует единственное решение y = y(x) этого уравнения, удовлетворяющее начальному условию (5).
Теорема 2. Пусть
функция f(x, y) непрерывна в прямоугольнике D = {x0 - a £ x £ x0
+ a, y0 - b £ y £ y0
+ b} и имеет в нем
ограниченную производную 
,
удовлетворяющую неравенству 
.
Тогда на отрезке s= [x0 - d, x0 + d], где 
,
где 
существует
единственное решение y = y(x) дифференциальное уравнение (4), удовлетворяющее начальным условиям (5). При
этом выполняется неравенство 
.
Решение y(x) - непрерывно дифференцируемо на s. Если f(x, y) имеет
непрерывные частные производные по x и y порядка
p, то y(x) имеет на sнепрерывные частные производные до порядка p + 1 включительно.
3. Дифференциальные уравнения с разделяющимися переменными.
ДУ с разделенными переменными называется уравнение вида
P(x) dx + Q( y) dy = 0, (1)
где P(x), Q( y) - известные функции. Интегрируя обе части уравнения (1) найдем общий интеграл ДУ (1).
.
(2)
ДУ с разделяющимися переменными называется уравнение вида
P1(x) Q1( y) dx + P2(x) Q2( y) dy = 0, (3)
где P1(x), Q1( y), P2(x), Q2( y) - известные функции. Разделим обе части уравнения на Q1( y)P2(x)
и интегрируем обе его части найдем общий интеграл ДУ (1).
.
(4)
При этом Q1( y)P2(x) = 0 дает особое решение ДУ (3).
К разделяющим уравнениям приводится решение следующих двух дифференциальных уравнений:
1) y' = f1(x) f2(у),
2) y' = f(ax + by +c).
При решении второго уравнения полагаем ax + by +c = u. Тогда 
и
данное уравнение приводится к виду
.
4. Однородные дифференциальные уравнения.
Определение 1. Функция f(x, y) называется однородной функцией n-го порядка, если f(lx, ly) = ln f(x, y). Если f(lx, ly) = f(x, y) = l0 f(x, y), то функция f(x, y) однородной функцией 0-го порядка.
Определение 2. Дифференциальное уравнение y' = f(x, y) называется однородным уравнением, если f(x, y) - однородная функций нулевого порядка.
Полагая l = 1/x, в силу
однородности функции f(x, y) получаем 
.
Тогда ДУ перепишем в виде 
.
Полагаем 
имеем
y = ux, y' = u'x + u. Тогда дифференциальное уравнение преобразуется в ДУ с
разделяющимися переменными.
Однородные ДУ иногда задаются в дифференциальной форме
P(x, y) dx + Q(x, y) dy = 0, где P(x, y), Q(x, y) - однородные функции одного порядка от переменных x, y.
Дифференциальное уравнение
можно превратить в однородное, при замене переменных x = u + a, y = v + b, где a, b находятся из решения системы линейных уравнений
.
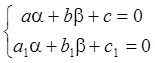5. Линейные дифференциальные уравнения первого порядка. Метод Бернулли. Метод Лагранжа.
Определение 1. Линейным дифференциальным уравнением первого порядка называется уравнение вида
y' + p(x)y = q(x), (1)
где p(x), q(x) - известные функции.
Метод Бернулли. Полагаем y = u v, где u = u(x), v = v(x). Тогда y' = u' v + u v' и уравнение (1) преобразуется к виду
u' v + u v' + p(x)uv = q(x), u' v + u(v' + p(x)v) = q(x).
Приравняем выражение в скобках к нулю и решим полученные дифференциальные уравнения
u' v
= q(x), v' + p(x)v
= 0, 
.
u' v
= q(x), 
Отсюда находим общее решение уравнения (1)
.
Метод Лагранжа (метод вартации произвольных постоянных). Решим сначала однородное ДУ соответствующее ДУ (1)
.
Заменяем в полученном решении однородного уравнения постоянную с функцией с(х) и ищем решение уравнения (1) в виде
.
Находим производную
.
Подставляем в уравнение (1) и получим
.
6. Уравнение Бернулли.
Определение 1. Уравнением Бернулли называется уравнение вида
y' + p(x)y = q(x)yn, n Î R., n ¹0, n ¹ 1. (1)
где p(x), q(x) - известные функции.
При n = 0 уравнение (1) - линейное первого порядка, n ¹ 1 - с разделяющимися переменными.
При n > 1 разделим обе части уравнения (1) на yn b уравнение
y' y-n + p(x)y-n+1 = q(x).
Полагаем y-n+1=z. Тогда получим
.
Получим линейное уравнение первого порядка
, решение которого удобно искать
в виде y = u v.
7. Дифференциальные уравнения в полных дифференциалах. Интегрирующий множитель.
Определение 1. Дифференциальное уравнение
P(x, y) dx + Q(x, y) dy = 0 (1)
называется дифференциальным уравнением в полных дифференциалах, если левая часть уравнения полный дифференциал от некоторой функции u(x, y), т.е.
P(x, y) dx + Q(x, y) dy = d u(x, y). (2)
Тогда
Теорема 1. Для того чтобы выражение D = P(x, y) dx + Q(x, y) dy, где функции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
