Линейные операторы. Определение линейного оператора и его свойства. Матрица линейного оператора, страница 2

Определение 3. Произведением AB линейных операторов A и B векторного пространства V называется отображение V в V, определенное для любого вектора, а из V по формуле: (AB)а = A(Bа).

Tеорема 1. 1. Сумма A + B двух линейных операторов A, B векторного пространства V линейный оператор векторного пространства V, и матрица линейного оператора A + B  равна A + B.

2.  Произведение aA числа a на линейный оператор A векторного пространства V линейный оператор векторного пространства V, и матрица линейного оператора aA равна aA.

3.  Произведение AB двух линейных операторов A, B векторного пространства V линейный оператор векторного пространства V, и матрица линейного оператора AB  равна AB.

4.  Характеристическое уравнение линейного оператора. Пусть V  - n - мерное векторное пространство над полем P, v =(v₁, v₂, …, v_n) - базис векторного пространства V, A - линейный оператор в векторном пространстве V, A - матрица линейного оператора A в данном базисе, l - переменная.

Определение 1. Характеристическим уравнением линейного оператора A называется уравнение

,

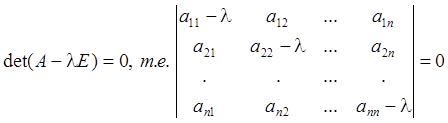Теорема 1. Характеристическое уравнение линейного оператора имеет степень n и не зависит от выбора базиса векторного пространства V.

5. Собственные векторы и собственные значения линейного оператора, и их связь с корнями характеристического уравнения. Пусть A - линейный оператор в векторном пространстве V над полем P.

Определение 1. Ненулевой вектор b называется собственным вектором линейного оператора линейного оператора A, если Ab = l b, lÎP. Число l называется собственным числом или собственным значением линейного оператора A.

Теорема 1.Число lÎP является собственным значением линейного оператора A тогда и только тогда, когда l корень характеристического многочлена линейного оператора A.

Собственные векторы линейного оператора A находятся из решения матричного уравнения

где B -координатный столбец собственного вектора b.

6. Линейные операторы  с простым спектром.

Определение 1. Пусть dim V = n. Если  линейный оператор A векторного пространства V имеет n попарно различных собственных значений, то он называется линейным оператором с простым спектром.

Теорема 1.Линейный оператор A n - мерного векторного пространства является линейным оператором с простым спектром тогда и только тогда, когда характеристическое уравнение линейного оператора имеет n попарно различных корней, принадлежащих полю P. 

Теорема 2. Линейный оператор A имеет в базисе v₁, v₂, ..., v_n диагональную матрицу тогда и только тогда, когда все вектора базиса являются собственными векторами линейного оператора A.

Доказательство. Необходимость. Пусть линейный оператор A имеет в базисе v₁, v₂, ..., v_n диагональную матрицу

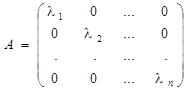 .                                                                          (1)

Тогда по определению матрицы линейного оператора имеем

Av₁ = l₁v₁ + 0×v₂ + ... + 0×v_n = l₁v₁, Av₂ = 0×v₁ + l₂v₂ + ... + 0×v_n = l₂v₂, …, Av_n = 0×v₁ + 0×v₂ + ... + l_nv_n = l_nv_n, и тогда по определению вектора v₁, v₂, ..., v_n являются собственными векторами линейного оператора A.

Достаточность. Пусть вектора базиса v₁, v₂, ..., v_n являются собственными векторами линейного оператора A, принадлежащими к собственным значениям l₁, l₂, ..., l_n. Тогда для них выполняются равенства (1) и матрица линейного оператора A в этом базисе диагональная. 

Теорема 3. Если вектора b₁, b₂, ..., b_k принадлежат к попарно различным собственным значениям линейного оператора A, то они образуют линейно независимую систему.

Доказательство. Доказательство теоремы проводим методом математической индукции по k . При k = 1 утверждение теоремы справедливо, так как собственный вектор b₁ ¹ 0 и образует линейно независимую систему.

Предположим, что утверждение теоремы верно для k - 1 векторов и докажем его для k векторов. По условию 

Ab_i = l_ib_i; i = 1, 2, ..., k,                                                                         (2)

где l_i ¹ l_j; i, j  = 1, 2, ..., k, i ¹ j. Пусть выполняется равенство:

a₁b₁ + a₂b₂ + ...+ a_kb_k = 0,                                                                         (3)

где a₁, a₂, ..., a_k Î Р. Покажем, что все a₁, a₂, ..., a_k  равны нулю. Действительно, если a_k = 0, то из (9) имеем a₁b₁ + a₂b₂ + ...+ a_k-1 b_k-1= 0 и в силу линейной независимости векторов b₁, b₂, ..., b_k-1(индуктивное предположение) все числа a₁, a₂, ..., a_k-1 равны нулю. Пусть a_k ¹ 0. Применяем к обеим частям равенства (3) линейный оператор A, используя свойства линейного оператора и равенства (2) получаем:

 a₁Ab₁ + a₂Ab₂ + ...+ a_k Ab_k = 0,   l₁a₁b₁ + l₂a₂b₂ + ...+ l_ka_kb_k = 0.

Умножая равенство (3) на l_k и вычитая почленно из последнего равенства, находим:

a₁(l₁-l_k)b₁ + a₂(l₂-l_k)b₂ + ...+ a_k-1(l_k-1-l_k)b_k-1 = 0.

Так как система векторов b₁, b₂, ..., b_k-1 линейно независима, то все числа a_i(l_i-l_k), i = 1,2, ...,k-1,  равны нулю. Так как по условию l_i ¹l_k, то l_i -l_k¹0 и a_i = 0, i = 1,2, ...,k-1, Тогда из (3) имеем a_kb_k = 0, a_k = 0и получаем противоречие. 

Теорема 4. Линейный оператор A с простым спектром имеет в некотором базисе диагональную матрицу.

Доказательство. Пусть A - линейный оператор с простым спектром, т.е. он имеет  n попарно различных характеристических корней , где n= dim V . По теореме 2 A имеет n попарно различных собственных значений l₁, l₂, ..., l_n , к которым принадлежат собственные вектора b₁, b₂, ..., b_n . По теореме 3 система векторов b₁, b₂, ..., b_n линейно независима, и образует базис V . Тогда по теореме 2 матрица линейного оператора A в этом базисе диагональная. Теорема доказана.

Следствие. Любая матрица А порядка n с элементами из поля Р, характеристический многочлен которой имеет nпопарно различных корней из Р, подобна диагональной матрице.