Приближенное решение уравнений. Отделение корней, страница 2

Чтобы можно было использовать этот метод, функция f(x) должна быть непрерывной и дважды дифференцируемой в интервале [a,b]. При этом могут представиться различные сочетания знаков производных и в интервале изоляции корня x^*, которые влияют на процесс отыскания приближенного значения корня методом хорд.

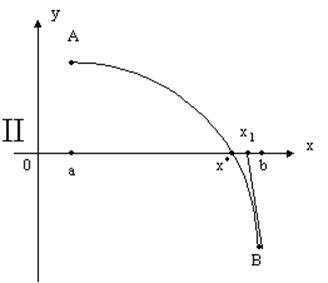
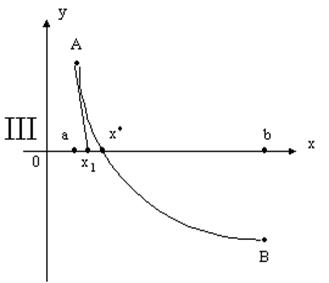
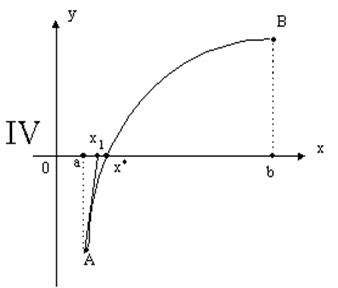
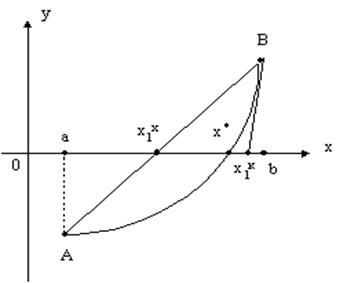
Проведем хорду AB, дуги AB кривой y=f(x). Абсцисса x₁ точки пересечения этой хорды AB с осью Ox будет первым приближением корня x^*.

(2)

или (3)

или (4)

Интервал изоляции [a;b] корня x^* можно сузить теперь до интервала [x₁;b] в случаях I, II и до интервала [a;x₁] в случаях III, IV. К новому интервалу изоляции [x₁;b] или [a;x₁] применим тот же прием проведения хорды. Для получения более точного второго приближения корня x^*, следует определить f(x₁).

Замечание. Знак f(x₁) всегда противоположен знаку на [a;b].

(5)

в случаях I и II,

(6)

в случаях III и IV.

На этом этапе интервал изоляции корня x^* можно сузить до интервала [x₂;b] в случаях I, II и до интервала [a;x₂] в случаях III, IV. Продолжая этот процесс, мы получаем все более точные значения корня x₁, x₂,? ,x_k.

Выясним теперь когда какую формулу применять. В случаях I, II и имеют одинаковые знаки на [a,b] (в I случае ; во II случае ), а в случаях III и IV - противоположные (в III случае ; в IV случае

Алгоритм метода:

1. Находим и . Определяем знаки и на [a,b].

2. В случаях I и II применяем формулу

(7)

В случаях III и IV

(8)

Корень x^* может быть вычислен методом хорд с любой степенью точности. Погрешность , где m - наименьшее значение модуля производной в интервале [a;b].

Пример: Методом хорд найти корень уравнения x³-3x²-13x-7=0 в интервале [-0.8;-0.6] с точностью e =0.0001.

Решение: f(x)=x³-3x²-13x-7, xÎ [-0.8; -0.6]. В этом интервале , (случай II), поэтому будем применять формулу (7):

f(-0.8)=0.968; f(-0.6)=-0.496; x₀=-0.8; b=-0.6.

; f(x₁)> 0.04541;

; f(x₂)> 0.00169;

; f(x₃)> 0.00014;

x^*> -0.66187.

п.4. Метод касательных. (Ньютона)

Метод касательных является одним из самых эффективных методов приближенного вычисления корня. Также как и метод хорд, метод касательных служит для уточнения корня x^* уравнения f(x)=0, для которого интервал изоляции [a;b] уже известен. Функция f(x) должна быть непрерывной и дважды дифференцируемой в интервале [a;b]. При этом могут представиться четыре различных сочетания знаков производных и в интервале изоляции корня x^*.

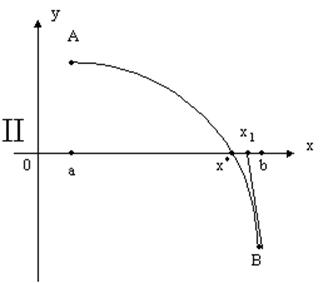
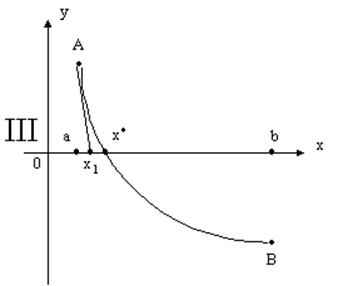
Проведем -касательную в точке B для случаев I, II и в точке A для случаев III, IV к кривой y=f(x). Абсцисса x₁ точки пересечения касательной с осью Ox будет равна

(9)

или (10)

соответственно.

Замечание. Значение x₁ может не принадлежать интервалу изоляции [a;b]. Поэтому надо правильно выбрать, в каком именно из концов дуги AB следует провести касательную, чтобы . Тогда x₁ будет первым приближением корня x^*.

Если f(b) и имеют одинаковые знаки (случаи I, II), то касательную следует провести в точке B. Тогда интервал изоляции корня x^* можно сузить до [a; x₁]. Если же f(a) и имеют одинаковые знаки (случаи III, IV), то касательную следует провести в точке A. Тогда интервал изоляции корня x^* можно сузить до [x₁; b].

К новому интервалу изоляции применим тот же прием проведения касательной и так далее, находя x₂,: ,x_n.

(11)

Корень x^* может быть вычислен методом касательных с любой степенью точности. Погрешность, как и в методе хорд, , где m - наименьшее значение модуля производной в интервале [a;b].