Генератор Ганна - это полупроводниковый прибор, действие которого основано на появлении отрицательного дифференциального сопротивления под воздействием сильного электрическою поля, предназначенный для генерации и усиления СВЧ - колебаний.
Рассмотрим вначале зависимостьr энергии свободного электрона, находящегося в вакууме, от его импульса P (рис. 7.1). Энергия такого электрона
![]() W
= m0vr2 =
m02vr2 =
Pr2 ,
(7.1)
W
= m0vr2 =
m02vr2 =
Pr2 ,
(7.1)
2 2m0 2m0
где vr - вектор скорости свободного электрона; m -0 его масса. Зависимость, представленная на рис. 7.1, является энергетической диаграммой свободных электронов в вакууме, изображенной в пространстве импульсов или в пространстве волновых векторов
r r = hkr = 2hπ kr).
k ( P
Рис. 7.1. Зависимость энергии свободного электрона, находящегося в вакууме, от его импульса
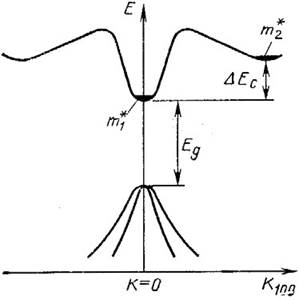
Рис. 7.2. Структура энергетических зон
арсенида галлия n-типа в кристаллографическом направлении [100]
В полупроводниковом кристалле свободный электрон можно считать свободным только условно, так как на электрон в кристалле действует периодическое потенциальное поле кристаллической решетки. Чтобы описать сложные законы движения электрона в кристалле с помощью соотношений, совпадающих по форме с законами классической механики, можно учесть влияние внутренних сил на электрон, изменив соответствующим образом значение его массы, т. е. введя понятие некоторой эффективной массы электрона (или дырки). Таким образом, эффективная масса - это коэффициент пропорциональности в законе, связывающем внешнюю силу, действующую на электрон в кристалле, с его ускорением.
Энергетическая диаграмманекоторых полупроводников, построенная в пространr
ствеквазиимпульсов (в k - пространстве), может иметь несколько минимумов. Например, в зоне проводимости арсенида галлия имеются два минимума, эффективные массы электронов в которых существенно различаются (рис. 7.2). Электроны, занимающие уровня, расположенные в центральном минимуме, называют легкими (т*1 = 0,072m0, m0 - масса свободного электрона), а в боковом минимуме - тяжелыми (т*2 = 1,2т0 ) . Так как подвижность обратно пропорциональна m*, то легкие электроны имеют высокую подвижность µ1 ≈ (5...8) •103 см2/(В•с), а тяжелые - низкую µ2 ≈ 100 см2/ (В•с).
Соотношение между концентрациями «легких» n1 и «тяжелых» п2 электронов изменяется при изменении напряженности электрического поля, так как в сильном электрическом поле (при напряженности, большей порогового значения Е > Eпор) электроны, приобретая дополнительную энергию, превышающую ∆Ec) (рис. 7.2), переходят в боковые долины и становятся «тяжелыми». Если при этом еще не происходит заметной ударной ионизации, то общая концентрация электронов остается неизменной и равной равновесной концентрации:
n1 + п2 = n0.
Обозначив подвижность «легких» электронов µ1, подвижность «тяжелых» электронов µ2 , выражение для плотности тока через кристалл запишем так:
J = q(n1µ +1 n2µ2)E . (7.2)
При слабых электрических полях (Е < Eпор) практически все электроны находятся в центральной долине, n1 ≈ n0 и плотность тока при этом J = qn0µ1E , что соответствует участку 1 ВАХ кристалла полупроводника (рис. 7.3). При сильных электрических полях (E >> Eпор) можно предположить, что практически все электроны приобретут добавочную энергию, большую ∆Ec , и окажутся в боковой долине. В этом случае n2 ≈ n0 и J = qn0µ2E , что соответствует участку 3. При средних напряженностях электрического поля, лишь немного превышающих пороговую, плотность тока
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.