Матрица, обратная Φ равна самой матрице, но с аргументом обратного знака, т.е.
Φ−1 ( )t = Φ(−t).
Для линейных систем переходная матрица представляет собой матричную экспоненту
![]() Φ( )t =
e At =
I +
At +
A t2 2 A tn n (4)
+Κ
+ .
Φ( )t =
e At =
I +
At +
A t2 2 A tn n (4)
+Κ
+ .
2! n!
Т.к. (4) удовлетворяет (3), действительно Φ&( )t = Ae At = AΦ .
Переходная матрица позволяет определить реакцию многосвязной системы на произвольные начальные условия.
Решение первого уравнения из системы (1) при произвольных начальных условиях тогда будет иметь вид:
t
![]() (5)
(5)
или выходная координата из второго уравнения (1)
t
y t( ) = x( )0 Ce At +![]() .
(6)
.
(6)
Модальные характеристики
Мода (англ.) – собственные значения и собственные вектора.
Модальные характеристики позволяют описывать собственные динамические свойства систем и находить свободную составляющую движения. Действительно, если объект описывается системой дифференциальных уравнений вида
при начальных условиях t0 = 0, x0 = x( )0 , то решение, как известно, имеет вид:
где xсв ( )t – свободная составляющая, xв ( )t –вынужденная составляющая.
Причем свободная составляющая получается из решения дифференциального уравнения.
x&= Ax . (3)
Решение (3) можно представить в виде:
Подставляя (4) в (3)
x( )0 λeλt = Ax( )0 eλt ⇒ (λI − A x) ( )0 = 0 (5)
Найдем λ и x(0) – соответствующие решению уравнения (5). Уравнение (5) будет иметь решение, если
Соотношение (6) представляет собой характеристическое уравнение, если раскрыть (6), то получаем:
anλ λn + an−1 n−1 + Κ + a1λ+ a0 = 0, (7)
где n – порядок дифференциального уравнения исходной системы (1).
Решения (7) λ1, λ2, ..., λn – корни характеристического уравнения (собственные значения матрицы A). Подставляя корни λi в уравнение (5), получим:
Можно определить значения всех компонент вектора x(0) – вектора начальных условий. Для λi
![]()
существует собственный вектор динамической системы – ei (i = 1,n).
Произведение eλit ei – мода системы.
Свободное движение динамической системы полностью определяется набором мод, т.е. существует определенная связь:
n
i=1
![]()
где fi – определяется заданными начальными условиями (i = 1,n) .
Часто для анализа свойств системы используют только собственные значения матрицы A (корни).
![]()
Как известно они могут быть: λi =±ai ± jbi , i = 1,n.
1. вещественные ± a1 ; ± a2 ; ± a3 ; Κ
2. комплексные ± a1 ± jb1; ± a2 ± jb2 ; ± a3 ± jb3; Κ
x1.1. Если все корни вещественны и отрицательны
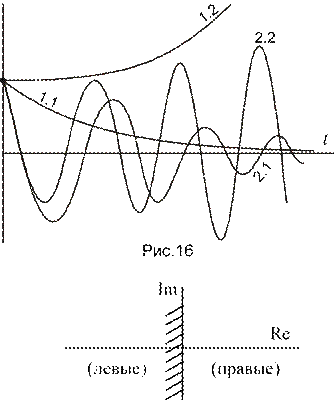
![]()
![]() λi
=−ai , i =1,n, тогда имеем
результирующую сходящуюся экспоненту (рис.16).
λi
=−ai , i =1,n, тогда имеем
результирующую сходящуюся экспоненту (рис.16).
1.2. Если среди отрицательных вещественных корней имеется хотя бы один положительный, то процесс будет соответствовать расходящейся экспоненте.
2.1. Если корни комплексные и все с отрицательной вещественной частью λi =−ai ± jbi , i =1,n , то процесс колебательный затухающий (сходящийся).
2.2. Если все корни комплексные и хотя бы один из них имеет положительную вещественную часть, то имеем расходящийся
колебательный процесс.
В ТАУ принято называть как вещественные, так и комплексные корни левыми, которые имеют отрицательную вещественную часть. Корни с положительной вещественной частью называются правыми. Их название ясно из рис.17.
Итак, для того, чтобы процесс был сходящимся (система линеаризованная была устойчива) необходимо и достаточно, чтобы все Рис.17 корни характеристического уравнения были левыми.
Кроме дифференциальных уравнений в ТАУ используются различные их преобразования, т.к. решение дифференциальных уравнений высокого порядка вызывает значительные трудности. Решения дифференциальных уравнений исследуются косвенными методами. Наиболее удобна алгебраизация дифференциальных уравнений.
Формальным обоснованием алгебраизации служит интегральное
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.