Расчет реакции опор нагруженного тонкого стержня, построение эпюр продольных сил и изгибающих моментов

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Комсомольский-на-Амуре государственный технический университет»

Кафедра «Промышленная электроника»

КОНСТРУКЦИОННЫЕ И БИОМАТЕРИАЛЫ

Контрольная работа

                                                 Группа 0БМб-1

Преподаватель: 

Студент:  В

Комсомольск-на-Амуре

2011

Содержание

1  Задание 1                                                                                                                   3                                                                                                                

2  Задания 2                                                                                                                   5

3  Задание 3                                                                                                                  7 

1 Задание 1

Дан нагруженный тонкий стержень. Рассчитать реакции опор, построить эпюры продольных сил и изгибающих моментов.

Таблица 1.1 – Данные к расчету

Рисунок 1.1 -  Схема задания

Решение:

Заменим рассредоточеную нагрузку сосредоточенной силой

 = q*d = 1.5кН и заменим опоры их реакциями .

Составим уравнение равновесия:

1)  Q+=0

2)  :

3)   

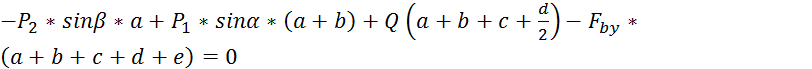
Из 2 уравнения имеем:

Из 3 уравнения имеем:

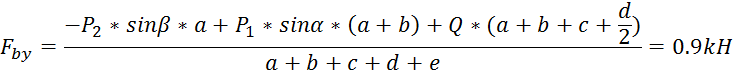
Из 1 уравнения имеем:

 - =0.3 kH

Для построения эпюры продольных сил разобьём балку на участки и вычислим данные продольной силы на каждом участке

 = -0.6 kH

= = -1.1kH

= 1.4kH

Построим эпюру изгибающих моментов, для этого выводим функции изгибающих моментов на каждом интервале:

Интервал (a+b+c+ )X(a+b+c+d+e)

=   

Интервал (a+b) (a+b+c+

=  + Q*(a+b+c-x)

Интервал ax(a+b)

= *(a+b+c+d+e-x)+Q*(a+b+c-x)-*(a+b-x)

Интервал  bxa

= *(a+b+c+d+e-x)+Q*(a+b+c-x) *(a+b-x)+*(a-x)

2 Задание 2

Дана система нагруженных тонких стержней. Рассчитать реакции опор, построить эпюры продольных сил и изгибающих моментов для стержня расположенного горизонтально. Принять α = 120º.

Таблица 2.1 – Данные к расчету

Рисунок 2.1 -  Схема задания

Решение:

Вместо опор проставим их реакции в итоге получаем балку с нагрузками

Рис 2.2 .

Составим уровнение равновесия

1)  ∑Fix=0: P3-FBx-FAx=0                                                            

2) ∑Fiy =0: FAy-P1+P2+FBy=0

3)  ∑MiA=0: P1*S1/2-P2*S1-FBx*S2/2*sin(180-α)-FBy*S2/2*cos(180-α)+P3*S2*sin(180-α)=0

Из 1 уравнения имеем:

FBx= Fax= =2кН

Из 3 уравнения получим:

FBу= 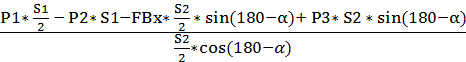 =4.5359кН

Из2 уравнения получим:

FAу= P1-P2-FBу= -3,5359кН

Далее рассмотрим горизонтальную часть балки и проставим реакцию опор: рис 2.3.

Составим уравнение равновесия и уравнение изгибающих моментов :

1)∑Fix=0: ∑Fсx- Fax=0

2) ∑Fiy=0: FAу-Р1+ Fсу+Р2=0

Оттуда получим

Fсx= Fax=2 кН

Fcy=Р1-Fay-P2=4,5359 кН

Продольные силы на участках будут:

Fпр1 = F пр2=Fcx=2 кН

Изгибающие моменты на участках будут:

при  < x < S1

M2=-(P2+Fcy)*(S1-x)

при 0<x<

M1=-(P2+Fcy)*(S1-x)+P1*( - x)

3 Задание 3

Дан нагруженный стержень переменного сечения. Построить эпюры продольных сил и нормальных напряжений. Рассчитать общее удлинение стержня. Принять модуль упругости первого рода Е = 2·10¹¹ Па.

Таблица 3.1 – Данные к расчету

Рисунок 3.1 -  Схема задания

Решение:

Для построения Эпура продольных сил вычислим продольные силы на участках

Pfg=P1=1кН

Pde=P1-P2=-2кН

Pbc=P1-P2-P3=-4кН

Pa=P1-P2-P3-P4=-6кН

Далее вычислим площади сечений

S1=πR1^2= 3.14

S2=πR2^2=28.26

S3=k^2=36

S4= =37.6

Тогда продольные напряжения будут:

δg==0.026 кН/

δf= =0.027 кН/

δe==0.055 кН/

    δd==0.070 кН/

δc==0.14 кН/

δb==1.27 кН/

δa==1.9 кН/

Далее вычислим удлинения:

Δ== м

= = 9.45*

= = 1.925*

= = 2.45*

= = 3.5*

= = 3.175*

= = 9.5*

=++++=