


Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего
Профессионального образования
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Кафедра теории рынка
Контрольная работа
По дисциплине: «Математические методы исследования экономики»
Вариант №2
Факультет: ВиЗОФБ
Группа: 001
Выполнила:
Проверил:
Новосибирск 2012
Задача 1.
Для заданной общей модели Леонтьева построить простую модель Леонтьева. Найти путь производства в единице каждого продукта. Определить минимальные затраты труда, необходимые для производства каждого продукта.
Для произвольного вектора выпуска решить двойственную задачу и определить теневые цены для каждого из продуктов.
Для варианта №2 даны следующие данные:
|
G0 |
G1 |
G2 |
G3 |
||||
|
P1 |
0,2 |
0,2 |
0,3 |
0,1 |
производит G3 |
||
|
P2 |
0,1 |
0,3 |
0,3 |
0,3 |
производит G2 |
||
|
P3 |
0,2 |
0,3 |
0,2 |
0,3 |
производит G1 |
||
|
P4 |
0,1 |
0,1 |
0,1 |
0,1 |
производит G3 |
||
|
P5 |
0,3 |
0,2 |
0,2 |
0,1 |
производит G2 |
||
|
P6 |
0,3 |
0,1 |
0,3 |
0,1 |
производит G1 |
Определим, какие технологические процессы следует включить в простую модель Леонтьева, т.е. будем минимизировать затраты труда при любом фиксированном ненулевом векторе выпуска.
Пусть хотим произвести набор продуктов y=(25, 50, 100)
0,2х1+0,3х2+0,1х3+0,3х4+0,1х5+0,2х6 → min
0,7х1+0,9х2-0,3х3-0,2х4-0,1х5-0,2х6=25
-0,2х1-0,3х2+0,7х3+0,8х4-0,1х5-0,3х6=50
-0,3х1-0,1х2-0,3х3-0,1х4+0,9х5+0,9х6=100
х1,х2,х3,х4,х5,х6 ≥ 0
Далее применим поиск решения:
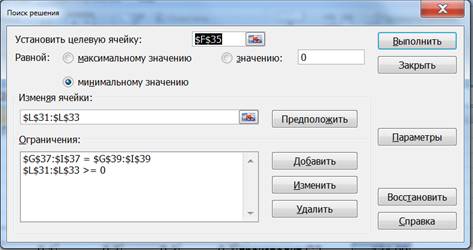
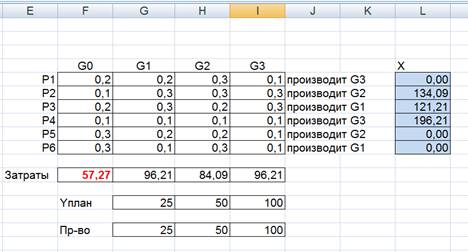
Далее построили простую модель Леонтьева (включили только процессы с положительными значениями интенсивности).
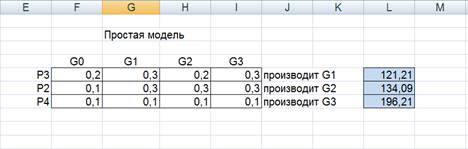
Найдем путь производства в единице каждого продукта:
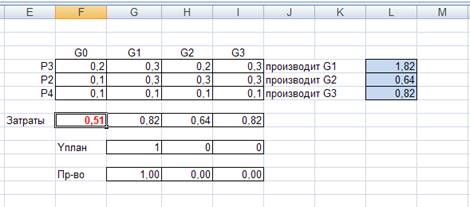
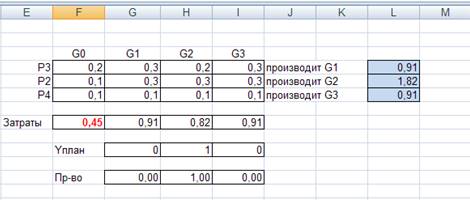
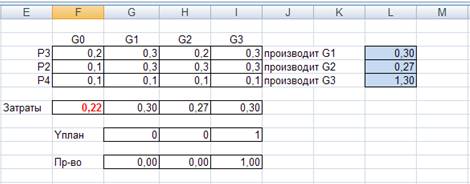
Можно сделать вывод, что минимальными будут затраты труда, необходимые для производства единицы продукта G3.
Прямая задача выглядит так:
0,2х1+0,1х2+0,1х3 → min
0,7х1-0,3х2-0,1х3=25
-0,2х1+0,7х2-0,1х3=50
-0,3х1-0,3х2+0,9х3=100
х1,х2,х3, ≥ 0
Двойственная задача выглядит следующим образом:
25р1+50р2+100р3 → max
0,7p1-0,2х2-0,3p3=0,2
-0,3р1+0,7р2-0,3р3=0,1
-0,1р1-0,1р2+0,9х3=0,1
р1,р2,р3, ≥ 0
Далее применим поиск решения:
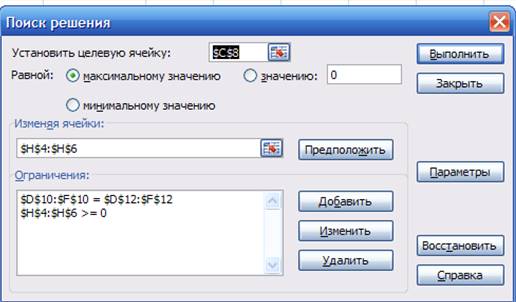
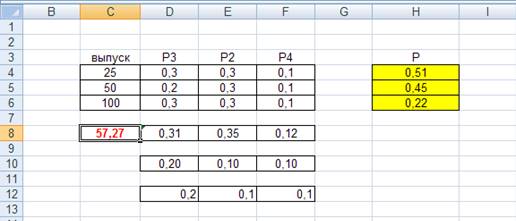
Решили двойственную задачу и определили теневые цены для каждого из продуктов.
Задача 2.
Для заданной экономической системы построить натуральную и стоимостную модели межотраслевого баланса. Вычислить матрицы прямых, полных и косвенных затрат.
Определить наиболее доходные (убыточные) отрасли с точки зрения государства и населения отрасли.
Для варианта №2 даны следующие данные:
Потребление в день:
Еда – 1, дрова – 2.
Возможное производство в день:
Еда – 16, дрова – 17, топоры – 7, бумеранги – 17.
Расход за один день деятельности:
При лесозаготовках топоров -1, на охоте бумерангов – 2.
Отдых после одного дня работы:
После охоты -0,5 , после лесозаготовок – 0,4 , после изготовлений орудий труда – 0,1.
Необходимо составить баланс на 344 дня.
Для потребления нам потребуется на весь период 344 ед.еды и 688 ед.дров.
Для производства 344 ед.еды потребуется 21,5 дней охоты, т.е. потребление в эти дни еды -21,5ед., дров – 43ед., бумерангов – 43шт., отдых – 10,75 св.дней.
Для производства 688 ед.дров потребуется 40,47 дней лесозаготовок, т.е. потребление в эти дни еды – 40,47 ед., дров -80,94 ед., топоров – 40,47 ед., отдых – 16,19 св.дней.
Для производства орудий труда нам потребуется 8,31 дней (2,53 дня для производства 43 бумерангов и 5,78 дней для производства 40,47 топоров). Понадобится 8,31 ед.еды и 16,62 ед.дров, отдыха - 0,83 св.дней.
1 тр.день=16 ед.еды=17 ед.дров = 7 топоров = 17 бумерангов , т.е.
1 ед.еды =0,063 тр.д.; 1 ед.дров =0,059 тр.д.; 1 топор =0,143 тр.д.;
1 бумеранг =0,059 тр.д.; 1 св.д. = 1ед.еды + 2 ед.дров = 0,181 тр.д.
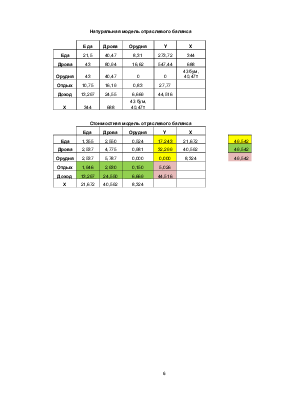
|
Натуральная модель отраслевого баланса |
|||||
|
Еда |
Дрова |
Орудия |
Y |
X |
|
|
Еда |
21,5 |
40,47 |
8,31 |
273,72 |
344 |
|
Дрова |
43 |
80,94 |
16,62 |
547,44 |
688 |
|
Орудия |
43 |
40,47 |
0 |
0 |
43 бум, 40,47т |
|
Отдых |
10,75 |
16,19 |
0,83 |
27,77 |
|
|
Доход |
13,297 |
24,55 |
6,669 |
44,516 |
|
|
Х |
344 |
688 |
43 бум, 40,47т |
||
|
Стоимостная модель отраслевого баланса |
|||||||
|
Еда |
Дрова |
Орудия |
Y |
X |
|||
|
Еда |
1,355 |
2,550 |
0,524 |
17,243 |
21,672 |
49,542 |
|
|
Дрова |
2,537 |
4,775 |
0,981 |
32,299 |
40,592 |
49,542 |
|
|
Орудия |
2,537 |
5,787 |
0,000 |
0,000 |
8,324 |
49,542 |
|
|
Отдых |
1,946 |
2,930 |
0,150 |
5,026 |
|||
|
Доход |
13,297 |
24,550 |
6,669 |
44,516 |
|||
|
Х |
21,672 |
40,592 |
8,324 |
||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.