Расчет одноступенчатого цилиндрического косозубого редуктора. Кинематический расчет привода. Определение требуемой мощности электродвигателя

Определение частоты вращения и угловой скорости каждого вала

 об/мин

Угловая скорость вращения вала шестерни, рад/с:

= 298,3 рад/с

Частота вращения вала колеса, об/мин:

 об/мин

Угловая скорость вращения вала колеса, рад/с:

 рад/с

Частота вращения вала исполнительного механизма, об/мин:

 об/мин

Угловая скорость вращения вала исполнительного механизма, рад/с:

 рад/с

1.4 Определение мощности на валах привода

Мощность на валу шестерни, кВт:

;следовательно

 кВт

Мощность на валу колеса, кВт:

 кВт

Мощность на валу исполнительного механизма, кВт:

 кВт

1.5 Определение крутящих моментов на валах привода

Крутящий момент на валу шестерни, Н ∙ м:

 Н ∙ м

Крутящий момент на валу колеса, Н ∙ м:

 Н ∙ м

Крутящий момент на валу исполнительного механизма, Н ∙ м:

 Н ∙ м

Вал	Р, кВт	n, об/мин	ω, рад/сек	Т, Н∙м	Примечание
1	2,2	2850	298,3	7,4	Вал шестерни
2	2,11	904,76	94,7	22,3	Вал колеса
3	1,96	285,4	29,87	65,6	Вал исполнительного  механизма
Uоткр пер=3,17

2 Расчет зубчатых передач

2.1 Расчет передач с цилиндрическими зубчатыми колесами

2.1.1 Выбор материала

Выбираем материал -  Ст 45.

Термообработка: улучшение.

Твердость зуба шестерня по Бринеллю – 280 НВ

Твердость зуба колеса по Бринеллю – 240 НВ

2.1.2 Определение допускаемых напряжений

где   – расчетная контактная прочность;

       – допускаемая контактная прочность.

Для колеса  , для шестерни :

где –  предел контактной выносливости (предельное напряжение);

       –  коэффициент запаса контактной прочности;

      –  коэффициент долговечности.

K_HL = 1 (по рекомендации)

S_H =1.1 – при нормализации, улучшении и объемной закалке.

Предел контактной выносливости, МПа:

Для шестерни, МПа:

 МПа

Для колеса, МПа:

 МПа

Допускаемая контактная прочность для шестерни, МПа:

 МПа

Допускаемая контактная прочность для колеса, МПа:

500 МПа

Расчетное допускаемое напряжение, МПа:

 МПа< Мпа

                               Верно!

2.1.3 Определение допускаемого напряжения изгиба при расчете на усталость

где   – расчетный предел выносливости;

       – допускаемый предел выносливости.

Для колеса  , для шестерни :

где –  предел выносливости по напряжению изиба;

      –  коэффициент безопасности;

     –  коэффициент долговечности;

    –  коэффициент, учитывающий влияние двухстороннего приложения нагрузки.

K_FL = K_FC =1 (по рекомендации)

S_F =1.75 – при нормализации и улучшении.

Для шестерни, МПа:

 МПа

Для колеса, МПа:

 МПа

Допускаемое напряжение для шестерни, МПа:

 МПа

Допускаемое напряжение для колеса, МПа:

246,86 МПа

2.2 Определение межосевого расстояния

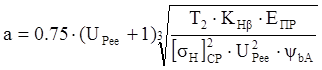
где – передаточное число редуктора;

       Н∙мм – крутящий момент на валу колеса; 

 МПа – расчетное допускаемое напряжение;              

       МПа – приведенный модуль упругости для стальных колес;

(по рекомендации)  –  коэффициент ширины колеса по межосевому расстоянию.

       – коэффициент ширины колеса по диаметру.

 – коэффициент концентрации нагрузки по длине зуба, определяем

 по таблице 2.4 [1]:

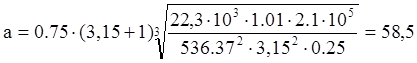 мм

Округляем до ближайшего стандартного по ГОСТ 2185-66:

 мм

2.3 Определение параметров зацепления и размеров зубчатых колес

2.3.1 Определение стандартного модуля зацепления m по ГОСТ 9563-60

2.3.2 Определение числа зубьев шестерни и колеса

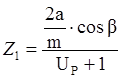
где β – угол наклона зубьев (принимаем 10° предварительно)

cos 10° = 0.9848

Число зубьев шестерни:

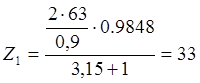
Число зубьев колеса:

Уточняем угол наклона зубьев β:

°

2.3.3 Определение геометрических параметров колес

Ширина колеса, мм:

 мм

Ширина шестерни, мм:

 мм

Делительный диаметр окружности шестерни, мм:

 мм

Делительный диаметр окружности колеса, мм:

 мм

Диаметр окружности выступов шестерни, мм:

 мм

Диаметр окружности выступов колеса, мм:

 мм

Диаметр окружности впадин шестерни, мм:

 мм

Диаметр окружностей впадин колеса, мм:

 мм

Проверка межосевого расстояния, мм:

 мм

2.4 Определение окружной скорости зубчатых колес и назначить степень точности передачи

Окружная скорость, м/с:

, м/с

где  – делительный диаметр окружности шестерни, м;

        – частота вращения шестерни, об/мин.

Степень точности 8 (средней точности).

2.5 Проверка прочности зубьев по контактным напряжениям

Допускаемое напряжение для косозубых колес:

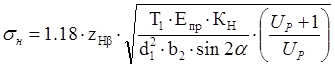
где  Н∙мм – крутящий момент на валу шестерни; 

       МПа

      – передаточное число редуктора;

       = 30,35– делительный диаметр окружности шестерни, мм;                                                                                

       мм – ширина колеса;

       ° - угол зацепления.

     

      -  коэффициент  расчетной нагрузки

где  - коэффициент динамической нагрузки, определяем по таблице 2,4 [1];

       - коэффициент концентрации, определяем по таблице 2,7 [1].

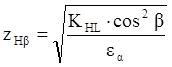
где  – коэффициент неравномерности нагрузки.

       – коэффициент торцового перекрытия.

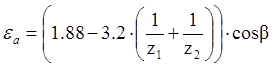
0,772

σ_н 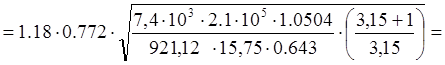437,4  МПа

на  % >15 – недопустимо

По рекомендации принимаем

σ_н 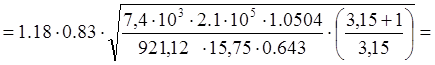470,7  МПа

 на  % <15 – допустимо

3 Проверочный расчет прочности зубьев по напряжениям изгиба

3.1 Определение сил, действующих зацеплений

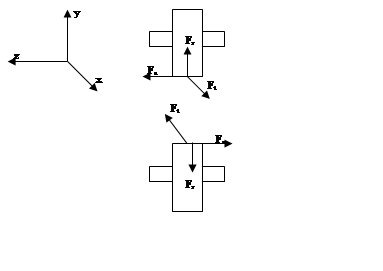
где  – осевая сила

       – радиальная сила

       – окружная сила

H

,

где  , т.к. °

H

где  , т.к.

 H

3.2 Определение нормальных напряжений при изгибе

Напряжение при изгибе

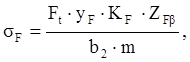
где  Н – окружное усилие;

 – стандартный модуль зацепления;

       – ширина колеса или шестерни;

       – коэффициент расчетной нагрузки;

       – коэффициент повышения прочности;

 – коэффициент формы зуба.

Расчет на изгиб проводится для того из колес зацепления, для которого отношение  - наименьшее.

3.2.1 Определение отношения для колеса и шестерни

Эквивалентное число зубьев шестерни:

35,2

Эквивалентное число зубьев колеса:

111

Коэффициент формы зуба шестерни:

 3.78

Коэффициент формы зуба колеса:

 3.6

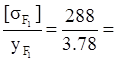 76,2

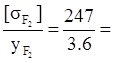 68.7 – расчёт ведём по колесу.

Расчет ведем для зуба колеса:

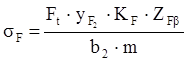
Коэффициент прочности зубьев:

где  – коэффициент распределения нагрузки по длине зуба;

       – коэффициент динамической нагрузки.

Коэффициент повышения прочности по напряжениям изгибов:

где  – коэффициент неравномерности нагрузки.

Коэффициент учитывающий повышение прочности на изгиб:

где  – угол наклона зубьев.

 МПа

 т.е.  – условие прочности выполняется.

4  Проектный расчет валов

4.1 Определение диаметра вала шестерни и колеса

4.1.1 Определяем диаметр вала шестерни

Для двигателя 80В2/2850  диаметр вала электродвигателя, мм:

 мм

Средний диаметр вала из расчета только на кручение при пониженных допускаемых значениях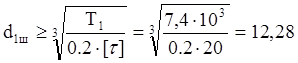, мм:

 мм

где =20 МПа – допускаемое напряжения для валов редукторов;

   мм

Принимаем:

Диаметр ведущего вала под подшипник, мм:

 мм

Диаметр ведущего вала под шестерней, мм:

 мм

4.1.2 Определяем диаметр вала колеса

Средний диаметр вала колеса из расчета только на кручение при пониженных допускаемых напряжениях, мм:

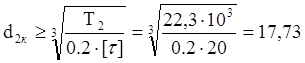 мм

Принимает:

Диаметр ведомого вала под колесом, мм:

 мм

Диаметр ведомого вала под подшипником, мм:

 мм

Диаметр выходного конца ведомого вала, мм:

 мм

Диаметр ступицы колеса, мм:

 мм

5 Уточненный расчет вала

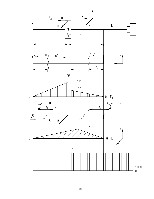
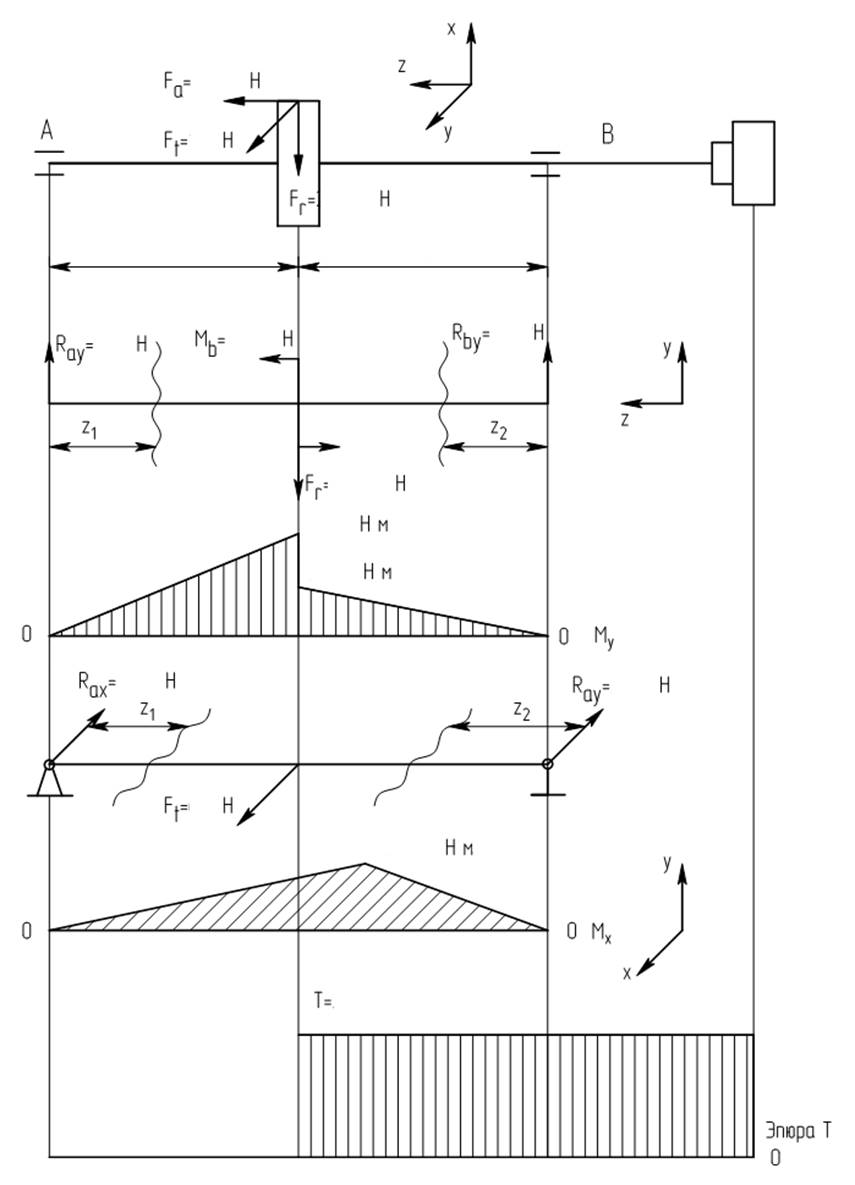
5.1 Построение эпюр  изгибающих моментов от сил действующих в вертикальной и горизонтальной плоскости, эпюры крутящего момента

 Н – окружная сила;

H – осевая сила;

H – радиальная сила.

Полная радиальная нагрузка на опору а, Н:

Полная радиальная нагрузка на опору b, Н:

R_bΣ =

Суммарный изгибающий момент, :

 мм

 Н∙мм,

где  мм – делительный диаметр окружности колеса.

5.1.1 Строим эпюру изгибающих моментов в вертикальной плоскости

Определяем опорные реакции, Н:

    

 Н

 

 Н

Проверка:

Строим эпюру изгибающих моментов, :

       

   

 

  

5.1.2  Строим эпюру изгибающих моментов от сил, действующих в горизонтальной плоскости

Определяем опорные реакции, Н:

Н

Строим эпюру изгибающих моментов, :

       

   

5.1.3  Строим эпюру крутящего момента

 Н∙м – крутящий момент на валу колеса.

5.1.4 Определение суммарного изгибающего момента

Суммарный изгибающий момент, :

 

5.2  Определение фактического коэффициента запаса усталостной прочности при совместном действии напряжений при кручении и изгибе

Фактический коэффициент запаса усталостной прочности при совместном действии напряжений при кручении и изгибе:

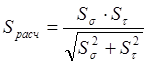
где  – коэффициент запаса усталостной прочности по нормальным напряжениям (от изгиба);

      – коэффициент запаса усталостной прочности по касательным напряжениям (от кручения);

Предел усталостной прочности материала вала при изгибе, МПа:

 МПа

где  = 600 МПа – предел прочности углеродистой стали;

Предел усталостной прочности материала при кручении, МПа:

 МПа

Коэффициент усталостной прочности по нормальным напряжениям при изгибе равен:

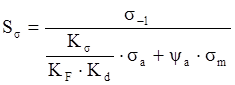
где ,– амплитуда напряжений от изгиба и кручения, МПа;

      ,  – среднее напряжение цикла при изгибе и кручении, МПа;

      ,  - коэффициенты концентрации напряжений;

       – коэффициент масштабного фактора;

       – коэффициент шероховатости поверхности.

Так как  – мало, то  =0

Амплитуда цикла напряжений при изгибе, МПа:

Момент сопротивления для круглого сечения при изгибе

 МПа

 – диаметр вала под колесом, мм

σ_a =  МПа

По таблице 3.1 [1] определяем эффективные коэффициенты концентраций напряжений при изгибе и кручении:

                

По таблице 3.2 [1] определяем масштабный коэффициент:

    

Коэффициент шероховатости поверхности:

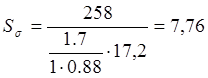
Коэффициент запаса усталостной прочности по касательным напряжениям при кручении:

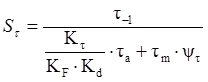
Амплитуда цикла напряжений при кручении, МПа:

,

где  – крутящий момент на валу колеса, Н∙мм;

       – момент сопротивления круглого сечения при кручении, .

По рекомендации принимаем коэффициент, корректирующий влияние среднего напряжения цикла на сопротивление усталости, равным:

ψ_τ = 0.05

 МПа

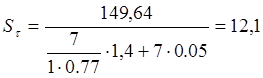
Фактический коэффициент запаса усталостной прочности:

S_расч = 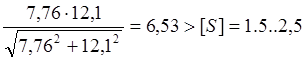 - условие прочности выполняется.

6 Элементы конструкции зубчатых цилиндрических колес

6.1 Определение размеров зубчатых колес

Диаметр ступицы, мм определяют

,

          где d – диаметр вала под колесом;

Длина ступицы, мм 

 ;      ;     

Толщина обода колеса, мм

Толщина диска, мм 

С=0,3b₂мм

 

Диаметр отверстий, мм 

;     

  ;     

 

7 Подбор и расчёт  подшипников  качения

Осевая сила F_а=98 H;

d_2п=20 мм;

Полная радиальная нагрузка на опоры:

ΣR_A===268,16 Н;

ΣR_В===236,72  Н;

По таблице П.3 выбираем:

серия подшипника №36204,

C=12,1  кH,

C₀=8,31  кH;

1)  Определение осевых составляющих S₁  и S₂ от радиальных нагрузок: