Достоинства синусоидальных токов и области применения. Изображение синусоидальных токов на комплексной плоскости, страница 2

17.Цепь синусоидального тока с индуктивностью.

Индуктивный элемент позволяет учитывать явление наведения ЭДС и явление накопления энергии в магнитном поле реальных элементов электрич цепей. Его характеризуют вебер-амперной характеристикой (зависимость Ф от i) или индуктивностью L=Ф/i. На схеме замещения индуктивную катушку можно представить в виде последовательно соединенных индуктвного и резистивного элементов. Приложим к индукт эл-ту синуоидальное напряжение u=U_msin(wt+j_u), тогда ток di=(1/L)udt, 

Синусоидальный ток в индуктивном эл-те: i=I_msin(wt+j_i), I_m=U_m/(wL); действующее значение I=U/(wL); где wL=X_L – индуктивное сопротивление, w=2pf (f-частота тока). Ток по фазе отстает от напряжения на p/2. j=j_u-j_I=p/2.

Заменим мгновенные значения напряжения и тока их комплексными выражениями:                                                , то по зак Ома                               падение напряжения                   ;  мгновенное значение мощности p= UIsin(2wt).

18.Цепь синусоидального тока с емкостным сопротивлением.

    Емкостной элемент – это идеализированный элемент цепи, по своим физич св-вам приближается к конденсаторам, он позволяет учесть протекание токов смещения и явление накопления энергии в электрическом поле реальных эл-тов электрической цепи. Его характеризует зависимость заряда q от напряжения u (кулон-вольтная характеристика) или ёмкость C=q/u. Если к емкостному эл-ту приложено синусоид напряжение u_C=U_msin(wt+j_u), то ток зарядки-разрядки емк                                                                                           

ток синусоидальный i=I_msin(wt+j_i); угол сдвига фаз м/у напряж и током  j=j_u+j_I=-p/2. Амплитуда тока I_m=wCU_m, а его действующее значение I=wCU; 1/(wС)=X_C – емкостное сопротивление. X_C=1/(wC)=1/(2pfC). Заменив мгновенные значения напряжения и тока комплексными выражен в показ-ной форме:

- по зак Ома .

Падение напряжения на участке цепи с емкостным эл-том в комплексной форме:

. В цепи содержащей емкость происходит преобразов эл-ой энергии в энергию электрич поля. p=UIsin(2wt). Качественно мощность на емкости характеризуется Q_C=I²/(wC) . Энергия электрич поля: W=CU²/2. Если проинтегрировать по времени обе части равенства                  , то получим                    .

Это равенство позволяет определить напряжение на конденсаторе через ток.

                                                                                      

19.Последовательное соединение цепи переменного тока.

- комплексное сопротивление;

                   - активное сопротивление;                                 - реактивн сопротивл;

                 - зак Ома для цепи синусоид тока.

20.Параллельное соединение в цепи переменного тока.

     Уравнение для мгновенных значений: i=i_a+i_L+i_C =

 u=Umsin(wt+j); В компл форме                       ;             

, где     - комплексное знач полной проводимости.

 

21.Векторная диаграмма для последовательной цепи.

Разделим векторн диагр напряж на вектор тока.

Умножим векторн диагр напряж на вектор тока.

P=Scosj; Q=Ssinj; S²=P²+Q². Полная мощность в комплексной форме определяется по формуле

, где -   сопряж значение комплексного тока. 

22.Векторная диаграмма для параллельной цепи.

   

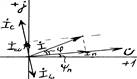
Разделим векторн диагр токов на вектор напряжения.

;     - компл знач полн сопротивл.

                                =g-j(b_L-b_C); g=R/Z²; b_L=(wL)/ Z²; b_C=1/(wC Z²); Z-модуль комплексной проводимости.

23.Эквивалентная схема замещения катушки индуктивности.

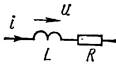
Реальная индуктивн катушка кроме индуктивн L обладает и активн сопротивлением R. Поэтому падение напряжения на реальной индуктивн катушке равно сумме напряж на L и R. Угол м/у напряж    и током  равен 90-d. tgd=                          ,  где Q_L – добротность реальной индуктивн катушки.

Чем больше Q_L, тем меньше угол d.

24.Эквивалентная схема замещения конденсатора.

При приложении синусоид напряж к пластинам конденсатора, разделенным твердым или жидким диэлектр, в последнем всегда имеются некоторые потери энергии, обусловл вязким трением при повороте дипольн молекул, а также несовершенством диэлектрика (налич у него небольш проводимости). Эти потери относит малы, и ими часто можно пренебречь. Если требуется учесть их в расчете, то конденс заменяют схемой замещения.   

1)Последовательная схема замещения.    -падение напряжения на реактивном эл-те;     - падение напряж на активном эл-те.

2)Параллельная схема замещения.

 

Угол d - угол диэлектрич потерь. Он зависит от сорта диэлектрика и частоты. 1/tgd=Q_C=(wC)/g – добротность конденсатора.