Расчет сборной предварительно напряженной арки пролетом 36м. Коэффициенты надежности по нагрузке и по назначению

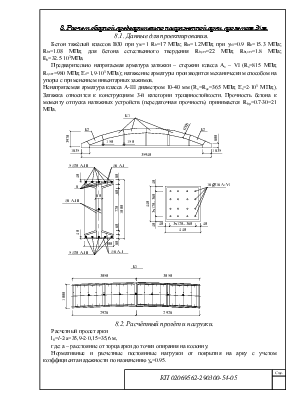
8. Расчет сборной предварительно напряженной арки пролетом 36м.

8.1. Данные для проектирования.

Бетон тяжёлый классов В30 при g_b1=1 R_b=17 МПа; R_bt=1.2МПа; при g_b1=0.9 R_b=15.3 МПа; R_bt=1.08 МПа; для бетона естественного твердения R_b,ser=22 МПа; R_bt,ser=1.8 МПа; E_b=32.5×10³МПа.

Предварительно напрягаемая арматура затяжки – стержни класса А_s – VI (R_s=815 МПа; R_s,ser=980 МПа; Е_s=1,9×10⁵ МПа); натяжение арматуры производится механическим способом на упоры с применением инвентарных зажимов.

Ненапрягаемая арматура класса А-III диаметром 10-40 мм (R_s=R_sс=365 МПа; Е_s=2×10⁵ МПа;). Затяжка относится к конструкциям 3-й категории трещиностойкости. Прочность бетона к моменту отпуска натяжных устройств (передаточная прочность) принимается R_bр=0.7×30=21 МПа.

8.2. Расчётный пролёт и нагрузки.

Расчетный пролет арки

l₀=l-2×a=35,9-2×0,15=35,6 м, где: а – расстояние от торца арки до точки опирания на колонну.

Нормативные и расчетные постоянные нагрузки от покрытия на арку с учетом коэффициента надежности по назначению g_n=0.95.

Расчетная постоянная нагрузка на 1 м с учетом веса арки G_n=400 кН

где g_f  и g_n – коэффициенты надежности по нагрузке и по назначению;

р – расчетная нагрузка на покрытие;

L – шаг колонн.

Расчетная временная нагрузка при S_n=1200 Н/м² для III снегового района.

S=S_n×L×g_n=1200×12×0,95=13680 Н/м=13,68 кН/м

8.3. Геометрические характеристики и усилия в сечениях арки.

Арку рассчитываем как двухшарнирную с затяжкой. Из соображений унификации блоков ось арки выполняют по круговому очертанию.

Находим геометрические характеристики арки; радиус оси круговой арки:

, где f – стрела подъема, принятая равной примерно 1/9 пролета, то есть 3,96 м;

Центральный угол

Длина арки

, где

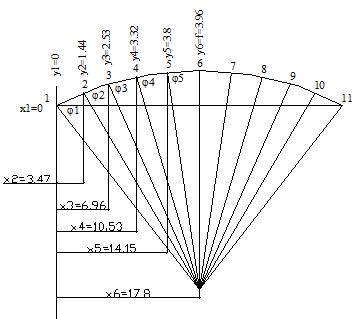
Арку разбиваем на 10 равных частей (дуге 0.1 части соответствует угол ) и определяем горизонтальные ординаты сечений по формулам

, где а=R-f=41,89-3,96=37,93 м

При j₁=25° (sin25°=0.4226; cos25°=0.9063):

;

;

при j₂=20° (sin20°=0.342; cos20°=0.9397):

м;

м.

Остальные значения x и y определяютcя аналогично.

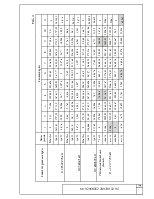
Величина y₀ соответствует длине стрелы подъема f. Результаты вычислений приведены в табл.1.

Табл.1

Предварительно задаемся площадями сечений арматуры в арке и в затяжке, а также вычисляем геометрические характеристики их сечений.

Принимаем приближенно для арки

А_s=0.01·A_b=0.01·(2×50×8+4×1/2×6×21+84×8)=0.01×1724=17.24 см²=1724 мм².

Принимаем А_s=1724 мм².

Отношение модулей упругости для арки

Тогда площадь приведенного симметрично армированного сечения арки

А_red=A_b+a×A_s+α·A¹_s=1724+5,85×17,24+5,85×17,24=1926 см² =19.26×10⁴ мм².

Момент инерции приведенного сечения при расстоянии до центра тяжести y_s=50 см

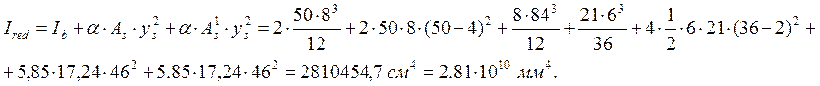
Радиус инерции приведенного сечения

.

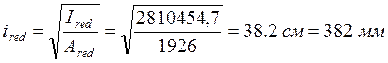Так как площадь сечения затяжки А₁=44×44=1936 см², то сечение арматуры принимаем приближенно

А_s1=0.01A₁=0.01×1936=19,36 см²»20 см²=2000мм².

Учитывая, что для отношения модулей упругости a=5.85, определяем площадь приведенного сечения затяжки

А_red1=1936+5.85×20=2053 см²=2.05×10⁵ мм².

Коэффициент податливости затяжки

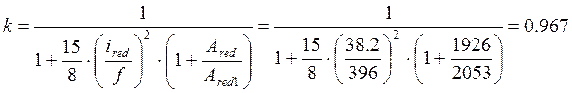
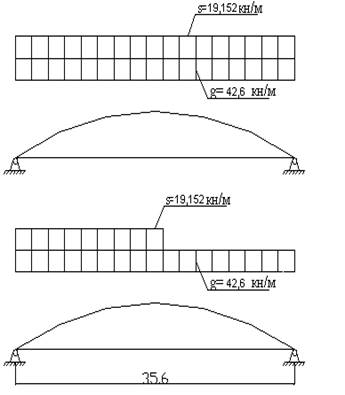
Для каждого случая загружения находим распор от нагрузки q=1000 Н/м, принятой за единичную:

ü  для равномерно распределенной нагрузки:

ü  для односторонней равномерно распределенной нагрузки на половине пролета арки:

По вычисленному распору для каждого вида загружения определяем расчетные усилия в сечениях арки. Для этого сначала определяем балочные изгибающие моменты М₀  и поперечные силы Q₀ .

При равномерно распределенной нагрузке балочные моменты и поперечные силы находим по формулам:

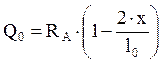  , где  – опорная реакция в балке.

Так, например, при х₆=17,8 м

;

При загружении половины пролёта арки балочный момент и поперечную силу в незагруженной части определяем по формулам:

М₀=R_B×x;  Q₀=R_B, где  – реакция в балке со стороны незагруженной части.

Например, при х₆=17.8 м;

М₀=4.45×17.8=79.21 кН·м.

После вычисления балочных моментов и поперечных сил по приведенным ниже формулам определяем расчетные усилия для всех сечений арки:

М_х=М₀-Н×у

N_x=Q₀×sinj+H×cosj

Q_x=Q₀×cosj-H×sinj

где j - угол между касательной к оси арки в рассматриваемом сечении и горизонталью;

M₀ и Q₀ – изгибающий момент и поперечная сила в балке на двух опорах пролетом, равным пролету рассчитываемой арки.

Определим M_x, N_x, Q_x  в середине пролета арки при действии равномерно распределенной нагрузки q=1000 Н/м  при j=0; М₀=158.42 кН·м; Q₀=0; Н=38.68 кН; у₆=3.96 м:

М₆=158.42-38.68×3.96=5.25 кН×м;

N₆=0-38.68×1=38.68 кН;

Q₆=0×1-38.68×0=0.

В табл. 2 приведены усилия от единичной нагрузки q=1000 Н/м, распределенной