Расчет деревянной крыши из сборных дощатых стропил. Расчет стропильного щита. Погонная нагрузка на один брусок

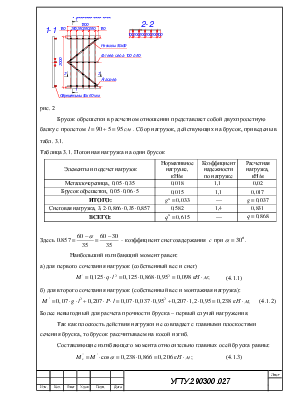
Нагрузку на второстепенную балку собираем с ее грузовой полосы, ширина которой равна шагу второстепенных балок  кроме того учитываем вес ребра балки.

Расчетные нагрузки:

постоянная: ;

временная: ;

полная: .

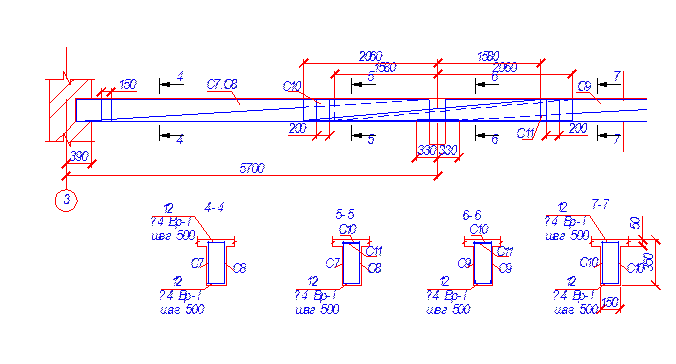
Расчетная схема балки и ее поперечное сечение

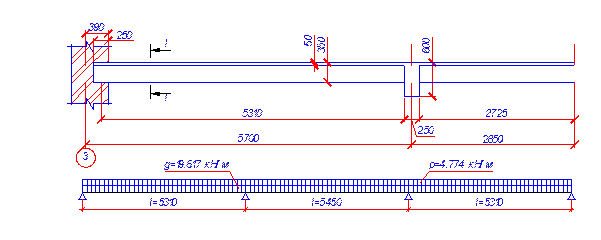
4.2.4.2 Определение расчетных усилий

Расчетные усилия в балке определяют с учетом их перераспределения.

Отношение временной нагрузке к постоянной: .

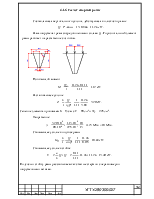
Так как во многих сечениях балки могут действовать изгибающие моменты с Разными знаками, то определение их только для основных пролетных и опорных сечений недостаточно. Необходимо вычислить положительные и отрицательные моменты для нескольких сечений балки по длине с целью построения огибающей эпюры моментов. При симметричной нагрузке и схеме балки расчетные усилия достаточно определить только для половины балки. Поскольку в данном случае разница в размере пролетов l₁ и l₂ меньше 10 %, используют формулы для равнопролетных балок.

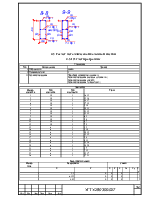
Таблица4.2.2  Изгибающие моменты в сечениях второстепенной балки

В первом пролете расстояние от правой опоры до нулевой ординаты отрицательных моментов:

.

В том же пролете расстояние от правой опоры до нулевой ординаты положительных моментов:

.

То же расстояние во втором пролете:

.

Вычисляем расчетные значения поперечных сил:

на крайней опоре: ;

на первой промежуточной опоре слева:

:

на первой промежуточной опоре справа:

.

4.2.4.3 Расчет прочности сечения

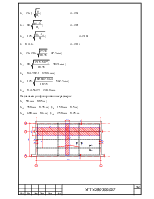
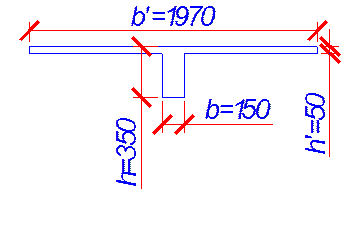
Размеры бетонного сечения второстепенной балки определены ранее – при компоновке монолитного перекрытия (). Для тех участков балки, где действуют положительные изгибаемые моменты, принимаем тавровое сечение с полкой в сжатой зоне. Вводят в расчет ширину сжатой полки , учитывая, что ширина свеса в каждую сторону от ребра должна быть не более 1/6 пролета, то есть:

.

Следовательно, для тавровых сечений балки: .

Рабочая высота сечений балки:

в крайних пролетах при а=0,05 м: ;

в среднем пролете при а=0,03 м: ;

у опор при а=0,05 м: .

Проверяем прочность бетона стенки по сжатой полосе между наклонными трещинами у первой промежуточной опоры слева, где действует наибольшая поперечная сила. Предполагаем отсутствие поперечной арматуры (для запаса прочности), при  проверяем условие:

, где  для тяжелого бетона.

;

.

Следовательно, принятые размеры бетонного сечения достаточны.

4.2.4.4 Расчет продольной арматуры

Определяем граничное значение относительной высоты сжатой зоны .

При ;

;

.

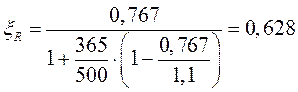Определяем положение нулевой линии в тавровом сечении балки. Наибольший положительный момент действует в крайнем пролете.

.

.

Нулевая линия расположена в полке, поэтому при действии положительных изгибающих моментов все сечения балки рассматриваем как прямоугольные шириной .

Определяем сечение продольной арматуры в пролетных сечениях балки при действии положительных моментов.

В пролете 1 при М=62,58 кН∙м

;

;

.

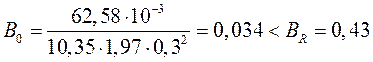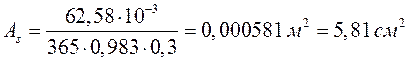В пролете 2 при М=45,28 кН∙м

;

;

.

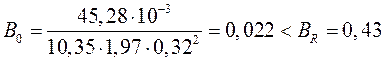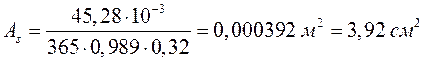В опорных сечениях балки действуют отрицательные изгибающие моменты, плита расположена в растянутой зоне, поэтому сечения балки рассматриваем как прямоугольные шириной b=0,15 м.

На опоре при М=-49,17 кН∙м

;

;

.

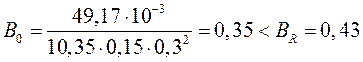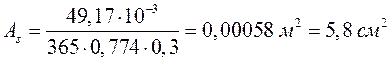4.2.4.5 Расчет поперечной арматуры

При .

Так как

, принимаем .

Проверяем условия:

;

для наклонных сечений балки у опоры А, где действует наименьшая поперечная сила.

;

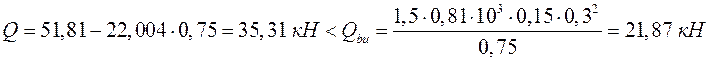 - не выполняется.

Необходима постановка поперечной арматуры по расчету.

Наибольшая поперечная сила (Q=77,71 кН) действует у опоры В слева. Поскольку на приопорных участках свесы полок в сжатой зоне отсутствуют, . требуемую интенсивность хомутов определяем из условий:

;

;

,

,

.

;

;

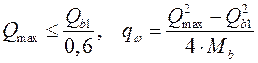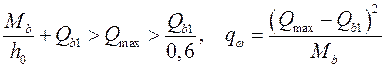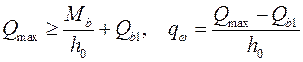 - не верно,

 - верно,

 - не верно,

.

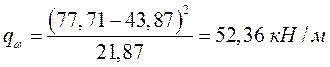Дополнительное условие:

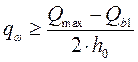
 - не верно.

Так как условие не выполняется, то

.

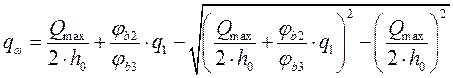
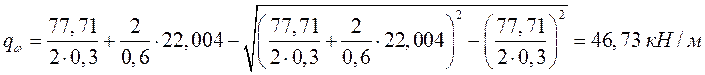Приминаем .

Назначаем шаг поперечных стержней. Наибольшее расстояние между ними:

.

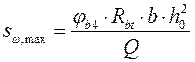
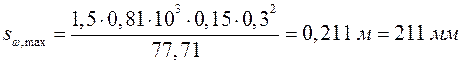При высоте сечения балки  шаг поперечных стержней должен быть не более  и 150 мм.

Принимаем шаг поперечных стержней 150 мм.

Требуемая площадь сечения хомутов:

.

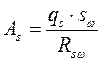
Принимаем 2Ø5 Вр1 с А_w=0,39 см² с шагом 150 мм.

Вычисляем, на каком расстоянии от опоры может быть увеличен шаг хомутов:

на приопорном участке: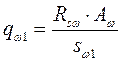

;

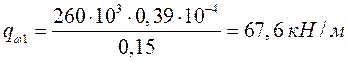на пролетном участке:

.

Так как

;

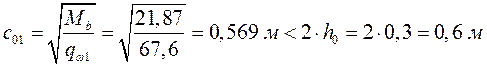, то

.

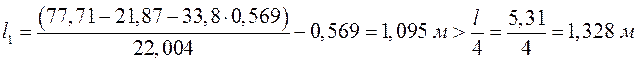У опоры В слева и у опоры А принимаем длину участка с шагом 150 мм равной 1,5 м, на пролетном участке 250 мм.

У опоры В справа (второй пролет) расчет выполняем в той же последовательности.

.

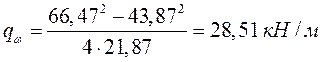 - не верно.

Так как условие не выполняется, то

.

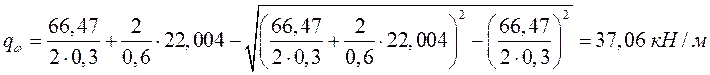Принимаем .

Требуемая площадь сечения хомутов:

.

Принимаем 2Ø5 Вр1 с А_w=0,39 см² с шагом 150 мм на опорном участке длиной 1,5 м, 300 мм на пролетном.

4.2.5 Расчет и конструирование главной балки

4.2.5.1 Расчетная схема

Расчетный пролет равен расстоянию между серединами площадок опирания балки на стену. Принимая длину опирания на стену для главной балки 0,3 м, получаем: