Практические задания.
1. Задание.
В. м- 4,5:
L. м – 3,5:
h, м - 4:
Снеговой район – 4 (2,4)
α - 350 С
Сечение балки - бревно:
Сечение колонны - квадратное.
2. Конструктивная схема стропильных ног.
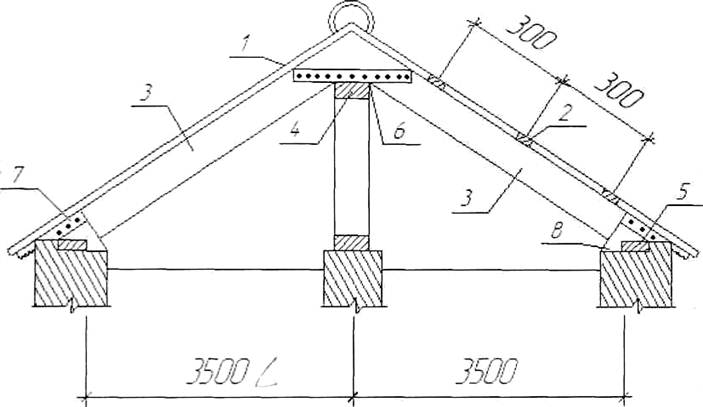
Простейшие наслонные стропила
1 - черепица; 2 - бруски обрешетки; 3 - стропильные ноги; 4 - прогон; 5 - мауэрлат; 6 - накладки 25х100 мм; 7 - кобылки 60х100 мм; 8 - скрутка из проволоки d = 4мм.
Расчетная схема.
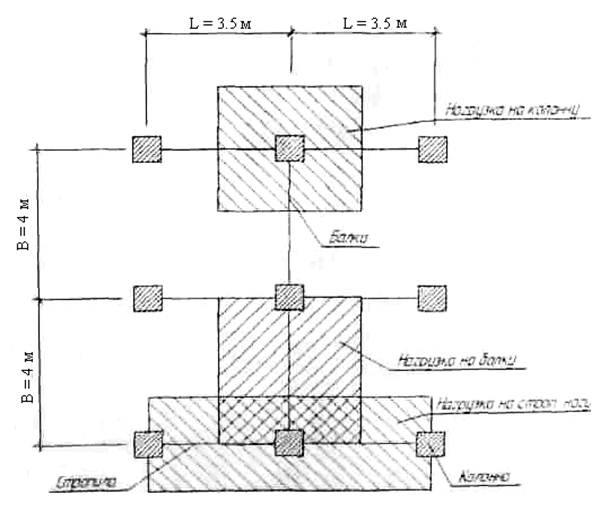
3. Подбор сечения наслонных стропил.
α - 350 С
1) Сбор нагрузок.
Вычисляем нагрузку, приходящуюся на 1 м2 горизонтальной проекции стропильной ноги.
|
№ п/п |
Нагрузки |
Подсчет |
Нормативная нагрузка, кПа |
Ч |
Расчетная нагрузка. кПа |
|
1 .Постоянные нагрузки |
|||||
|
1 2 3 |
Черепица t = 0,03 м: р=2900 кг/м3 Обрешетка t = 25 мм; р=550 кг/м3. Строп, нога, ориентировочно сечением 20*30 см; р=500 кг/м3. |
|
1,06 0,17 0,37 |
1,1 1,1 1,1 |
1,17 0,19 0,41 |
|
qn =1,6 |
q =1,77 |
||||
|
2.Временные нагрузки |
|||||
|
1 |
Снеговая нагрузка 4 снеговой регион |
S=Sg; Sn=Sg*0.8= 2,4*0,8 = 4,48 |
Sn = 1,92 |
— |
S =2,4 |
|
Итого: |
gn= 1,92 |
g =2,4 |
|||
|
Всего: |
gстр. ноги = 3,52 |
gстр. ноги = 4,17 эСТр.НОГИ О.ЧЛ Kl id |
|||
Полная нагрузка, приходящаяся на погонный метр горизонтальной проекции стропильной ноги с учетом коэффициента надежности по ответственности:
γn = 0,95
q = 4,17 *3.5*0.95=24.32 кН/м
qn = 3,52*3.5*0.95= 19.85 кН/м
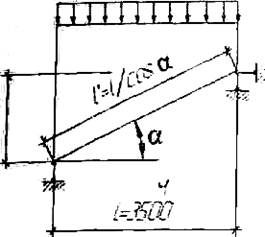
2) Наибольший изгибающий момент при свободном опирании стропильной ноги на двух опорах:
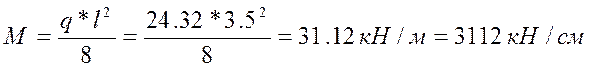
3) Требуемый момент сопротивления:
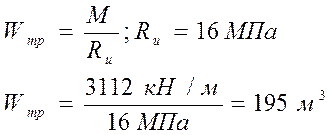
4)
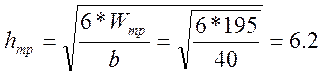
Принимаем по сортаменту размеры сечения 100*250 мм, с F=250см2; b=100 мм; h=250 мм.
5)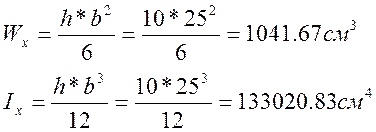
6) Определяем длину стропильной ноги по скату:
I' = l/Cosα,; cosα = cos35° = 1' = 3.5 м/0,819 = 7.
7) Напряжение
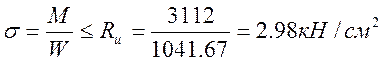
8)
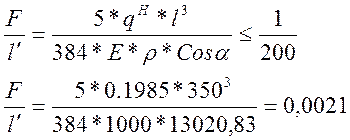
0,0021<0,005 - верно!
Условие выполняется.
4. Подбор сечения балки.
|
№ п/п |
Нагрузки |
Подсчет |
Нормативная нагрузка, кПа |
Ч |
Расчетная нагрузка. кПа |
|
1 .Постоянные нагрузки |
|||||
|
1 2 3 |
Черепица t = 0,03 м: р=2900 кг/м3 Обрешетка t = 25 мм; р=550 кг/м3. Строп, нога, ориентировочно сечением 20*30 см; р=500 кг/м3. |
|
1,06 0,17 0,37 |
1,1 1,1 1,1 |
1,17 0,19 0,41 |
|
qn =1,6 |
q =1,77 |
||||
|
2.Временные нагрузки |
|||||
|
1 |
Снеговая нагрузка 4 снеговой регион |
S=Sg; Sn=Sg*0.8= 2,4*0,8 = 4,48 |
Sn = 1,92 |
— |
S =2,4 |
|
Итого: |
gn= 1,92 |
g =2,4 |
|||
|
Всего: |
gстр. ноги = 3,52 |
gстр. ноги = 4,17 эСТр.НОГИ О.ЧЛ Kl id |
|||
q = 4,17 *3.5*0.95=24.32 кН/м
qn = 3,52*3.5*0.95= 19.85 кН/м
2) Определяем изгибающий момент:
![]()
![]()
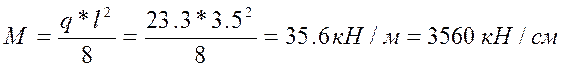
3) Принимаем породу древесины, сорт, температурно-влажностный режим:
Материал: кедр сибирский; сорт - 2; температурно-влажностные условия эксплуатации -А2.
Коэффициент условия работы mВ =1,0 (СНиП II - 25 - 80). Сечение бревна - круглое.
Расчетное сопротивление изгибу Ru=16 МПа=1,6 кН/см2. Расчетное сопротивление скалыванию RCK=1,6 МПа=0,16 кН/см2.
Переходный коэффициент от древесины сосны, ели к древесине кедра mП=0,9
Расчет сопротивления с учетом коэффициента mП равны:
Ru = 16 * 0.9 = 14.4 МПа = 1,44 кН / см2
Rск = 1.6 * 0.9 = 1.44 МПа = 0.144 кН /см2
4) Определяем требуемый момент сопротивления
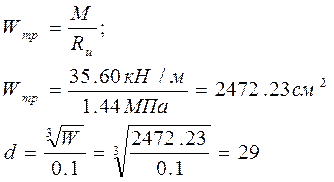
Принимаем сечение балки с учетом размеров, приведенных в сортаменте: принимаем d = 30 см.
5)W=0.1d3; W=0.1*303=2700 см3
6) Проверяем прочность по уровням:
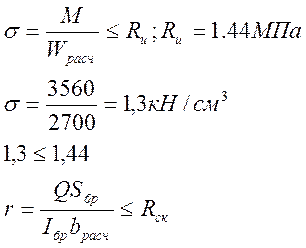
Iбр- момент инерции
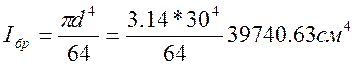
Q- расчетная поперечная сила
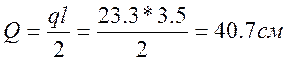
Sбр – статический момент
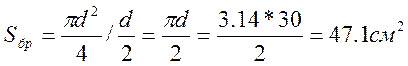
bрасч = d = 30см
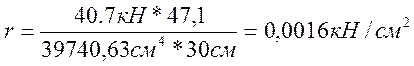
0,0016кН/см2≤0,144кН/см2
7) Проверяем жесткость:
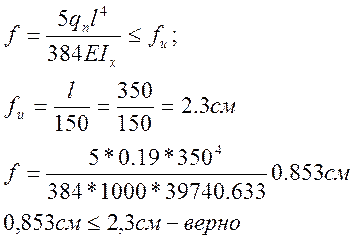
5. Подбор сечения колонны.
 1) Определяем нагрузку,
которая действует на стойку:
1) Определяем нагрузку,
которая действует на стойку:
N=mкровлиSкровли
S=bL=4,5 м*3,5 м = 14 м2.
N= qS = 23,3 кН/м * 14 м2 = 326,2 кН
2) Определяем расчетную длину стойки:
![]()
![]()
μ=1 - принимается в зависимости от степени подвижности опоры (т.5.1 Сетков).
1о=1*5 м = 5 м = 500 см.
3) Принимаем породу древесины, сорт.
Материал: сосна, сорт I.
4) Определяем расчет сопротивления древесины на сжатие Rс (СНиП II - 25 - 80).
Rс=16МПа =1.6кН/см2.
5) Задаемся % продольного изгиба, который может быть:
Φ =0,6*0,7
6) Определяем требуемую площадь поперечного сечения колонны:
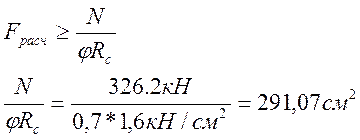
7) По найденной площади назначаем размеры поперечного сечения:
![]() -
для квадратного сечения.
-
для квадратного сечения.
![]()
Принимаем сечение 175*175 мм с учетом сортамента; с фактической площадью F = 306,25 см2.
8) Определяем радиусы инерции и проверяем условие, ограничивающее гибкость:
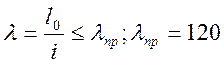
i- радиус инерции
ix=0.289h=0.289* 17.5 см =5.06 см.
iy =0.289h=0.289*17.5см =5,06см.
1о = 5 м = 500 см
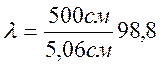
98.8≤120 - верно
9) Проверяем устойчивость принятого сечения:
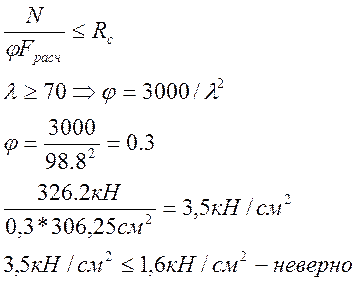
10) Увеличиваем размеры сечения и снова делаем проверку.
Принимаем сечение 200*200 мм, с фактической площадью F = 400 см2.
11 )Определяем радиусы инерции и проверяем условие ограничивающее гибкость.
ix = iy=0.289h=0.289*20 см = 5,78 см.
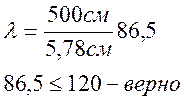
12) Проверяем устойчивость принятого сечения:
λ >70 =>φ = 3000/λ2 .
![]()
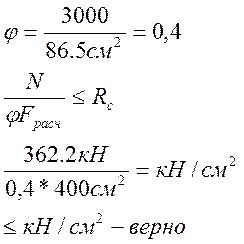
Условие устойчивости удовлетворено и сечение не имеет ослаблений, следовательно, расчет окончен.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.