Фазовая синхронизация. Синхронная машина, как аналог фазового детектора. Статическая синусоидальная угловая характеристика синхронной машины

Лекция 9

Глава5. Фазовая синхронизация

5.1. Краткая история проблемы

Решением проблемы фазовой сихронизации электоромеханических систем научная школа кафедры САУ занималась более 40 лет. Кроме решения ряда важных  научно - прикладных задач, нами были созданы и введены в постоянную промышленную эксплуатацию многочисленные электромеханические комплексы (ЭМК) для поверки и аттестации навигационной аппаратуры для  летательных аппаратов и изделий ракетно - космического комплекса страны. Высшим достижением нашего научно - технического и инженерного творчества являются  государственные эталоны "линейных  ускорений твердого тела" и "перемещений скоростей и ускорений твердого тела при колебательном движении", установленные в Российском Институте Метрологии им Д.И. Менделеева (СПб ). Рис.1. 9

Одновременно (при незначительных контактах с нами) начинал свои работы "по математической теории фазовой синхронизации" в 70 -е годы в Ленинградском Государственном Университете (ЛГУ) будущий член. - корр. РАН Геннадий Алексеевич Леонов. Рис.2. 9.Такова, кратко, история вопроса.

Электротехническую основу ЭМК составляют прецизионные (точные) системы стабилизации угловой скорости рабочих органов  комплекса  и их электроприводов.

Созданные нами  установки не имеют равных себе ни по диапазонам регулирования скорости (до 1:10⁶) и по точности стабилизации скорости (до 1.10^-4  - 1.10^-5) %, ни по равномерности медленных вращений (примерно 1оборот\в год).

В большинстве прецизионных замкнутых систем электропривода заложен принцип фазовой синхронизации, основным элементом которой является фазовый детектор.

Рассмотрим фазовый детектор (аналог синхронной машины)

5. 2 Синхронная машина, как аналог фазового детектора

Рассмотрим математическую модель установившегося (синхронного) движения такой машины. Обычно её называют "угловой характеристикой "(Рис.3. 9)

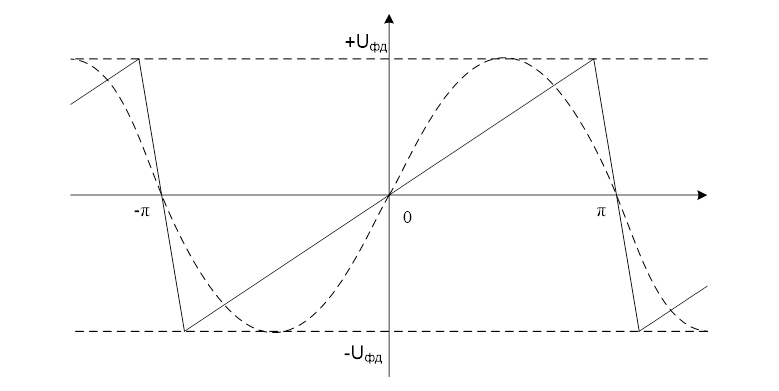Рис.3. 9. Статическая синусоидальная угловая характеристика синхронной машины.

Рис.1.9

Кстати, профессор А. А. Горев (ЛПИ) в (50 - 60)г.г. XX в. много занимался проблемами устойчивости синхронных машин, существует система уравнений Горева-Парка..

Но мы воспользуемся  работой Трикони (Италия), который записал уравнение синхронной машины в таком виде:

                                               (1. 9)

где - синхронный момент,  - асинхронный (синхронизирующий) момент.

Скорость вращения ротора  и скольжение

, где  - число пар полюсов машины

                                (2. 9)

Уравнение (2. 9) может быть переписано в ином виде:

                                                                       (3. 9.)

Уравнение (3. 9) может быть переписано в канонической форме, что позволяет представить траектории движения его координат в фазовой плоскости. Обозначим:

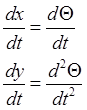
Следовательно:

,                                                                              (4. 9)

где  - возможное изменение скорости машины - "полоса удержания"

 - величина скорости ротора машины  при которой он (ротор) "втягивается"в синхронизм

Рис.2. 9

Исследуя  эту модель синхронной машины, Г.А. Леонов в одной из своих последних работ (Фазовая синхронизация. Теория и приложения. "Автоматика и телемеханика № 10,2006.) показал, что могут возникать в этой нелинейной динамической системе различные режимы движений.

Режим Глобальной устойчивости (Рис.4. 9)  Система  может проскальзывать в своем синхронном движении на угол "" (электрических)

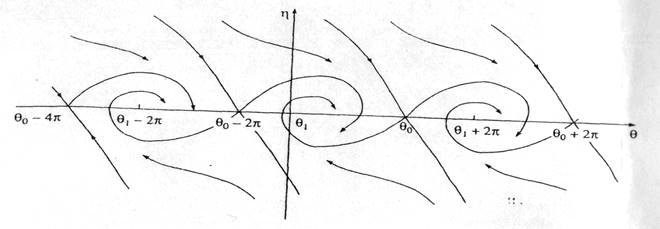
Рис. 4. 9. Глобальная устойчивость периодических движений фазовой системы - синхронной машины при угле нагрузке  

Гомоклиническая бифуркация

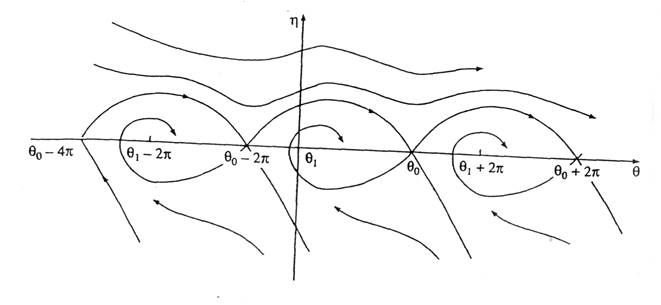
Рис. 5. 9. Гомоклиническая бифуркация периодических движений фазовой системы - синхронной машины при угле нагрузке  и .

Случай α < α(γ)

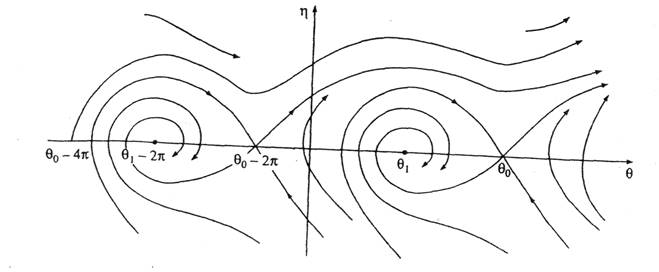
Рис. 6.9. Неустойчивые периодические движения

Вернемся вновь к рис.3. 9. Синхронный двигатель имеет рабочую зону  угла ,играющего роль внутреннего фазового детектора (ФД), равную π. Желательно расширить её. Для этого необходимо  внутренние электромагнитное взаимодеиствие между ротором и статором машины осуществляемое через угол   вынести во внешнии контуры управления , создав внешний  фазоывй детектор Это можно сделать только  в синхронизированной электрической машине с внешним фазовым детектором. Характеристика такого ФД изображена на рис .3. 9 прямыми ломаными линиями

Кроме того, в точном электроприводе желательно иметь многополюсную синхронную машину, что конструктивно сложно и дорого. В синхронизированной машине эта проблема вполне решаема.

3. 9. Гармоническая линеаризация периодических нелинейностей второго рода

Модели фазовых систем с периодическими нелинейностями имеют обычно больший порядок , чем рассмотренная выше модель второго порядка .Такие модели можно гармонически линеаризовать, но только специальным образом со сдвигом входного гармонического сигнала на угол 2π радиан за время Т.

, где   

Необходимо найти коэффициенты такой линеаризации: , и

Эти работы выполнены только на нашей кафедре.

4. 9. Система фазовои синхронизации с машиной постоянного тока .

Структурная схема системы фазовой синхронизации изображена  нна рис 7.9

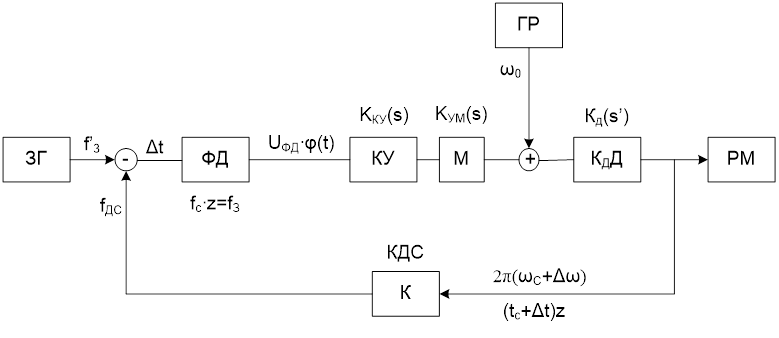
Здесь принято:z – число делений датчика скорости, КУ – корректирующее устройство, ДС – датчик скорости,ГР – грубый регулятор.. ЗГ задающий генератор, ФД фазовый детектор

, ,

С помощью ГР можно поддерживать скорость на заданном уровне, поднимая/опуская механическую характеристику двигателя (рис 8. 9).

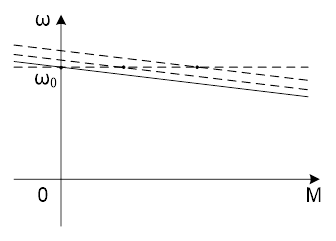
Рис. 8. 9 Механические  характеристики

Фазовой системы

, где

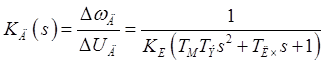 - ПФ датчика скорости

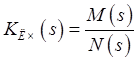
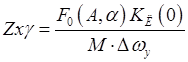            (1)

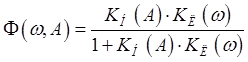
В замкнутой системе знаменатель должен равняться нулю

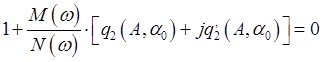
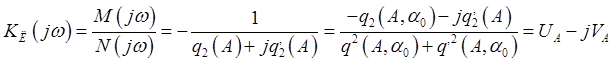
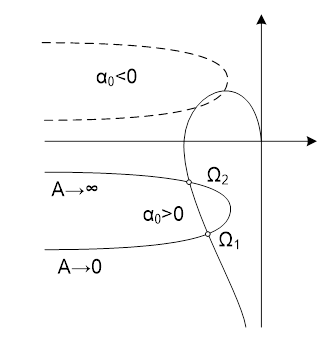
При  режим автоколебаний получить сложнее. Автоколебаний может не возникнуть.