Динамические свойства механической части электропривода. Корни характеристического уравнения

Лекция 3

Динамические свойства механической части электропривода

Полученные уравнения движения позволяют проанализировать динамические особенности механической части электропривода как объекта управления. Основой для анализа являются структурные схемы, вид которых определяется принятой расчетной схемой механической части.

Для получения структурной схемы трёхмассовой упругой механической системы используем (2-15) и (2-16) и полагая , получим

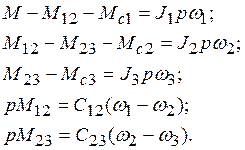                               (3-1)

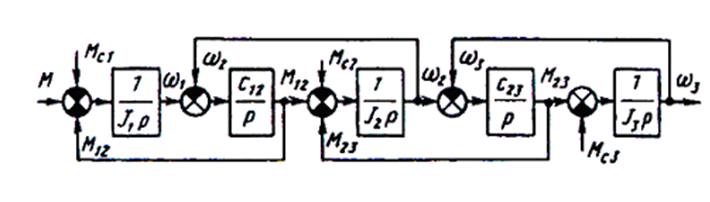
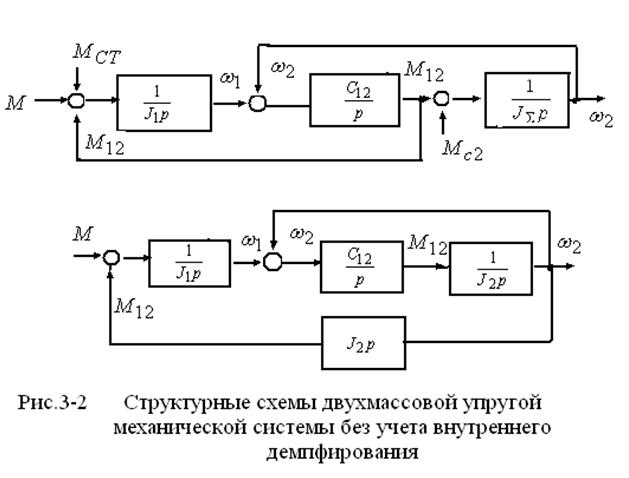
Системе уравнений (3-1) соответствует структурная схема, приведенная на рис. 3-1.

Управляющим воздействием здесь является электромагнитный момент двигателя М, а возмущениями — моменты нагрузки .  Регулируемыми переменными могут быть скорости , перемещения ,  а также упругие  моменты . Структурно механическая часть электропривода представляет собой сложный объект, состоящий из цепочки интегрирующих звеньев, замкнутых перекрестными внутренними обратными связями

Передаточная функция этой системы по управляющему воздействию

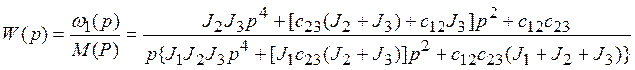.   (3-2) Характеристическое уравнение имеет вид

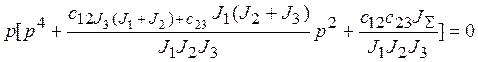
Решив это уравнение, получим корни характеристического уравнения системы

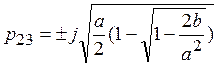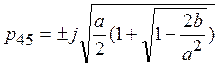 ;  , где ,   .

Анализ корней показывает, что при всех реальных сочетаниях параметров подкоренные выражения представляют собой действительные положительные числа. Следовательно, .

Корни характеристического уравнения свидетельствуют о том, что система содержит два колебательных звена с резонансными частотами  и . При ступенчатом изменении момента М(р) в системе могут возникать незатухающие колебания с частотами и , а когда частота возмущающих воздействий совпадает с одной из этих частот, в системе развивается недемпфированный резонанс, при котором амплитуды колебаний теоретически могут возрастать до бесконечности. Реально в системе присутствуют диссипативные силы, которые демпфируют колебания, ограничивая амплитуды резонансных колебаний.

Более детальный анализ свойств упругих механических систем удобно  провести на основе двухмассовой расчетной схемы, структура которой представлена на рис.3-2. Она составлена на основе  (3-1) при   .  Для исследования свойств этой системы как объекта управления примем возмущения  и выполним показанные на рис. 3.2  преобразования ее структуры. Далее находим передаточную функцию двухмассовой системы по управлению при выходной переменной  

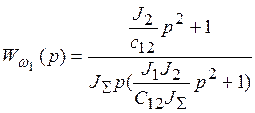                                        (3-3)

Характеристическое уравнение системы имеет вид:                              

.

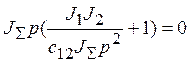Корни характеристического уравнения

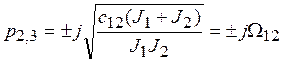  ,                (3-4)

где  — резонансная частота двухмассовой упругой системы.

Передаточная функция, связывающая выходную координату со скоростью :

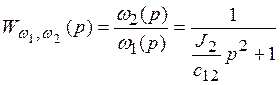.                            (3-5)

При переходе от трехмассовой упругой системы к двухмассовой выявляется только одна частота , на которой возможно проявление механического резонанса. Однако если при этом значение  оказывается достаточно близким к одной из частот исходной системы  или , можно полагать, что двухмассовая система правильно отражает главные особенности механической части электропривода.

Для удобства анализа введем следующие обобщенные параметры двухмассовой упругой системы:

 соотношение масс;

 - резонансная частота системы;

 резонансная частота второй массы при жестком закреплении  первой ().

С учетом этих обозначений (3-3) и (3-5)  могут быть представлены в виде

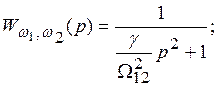                                (3-6)   

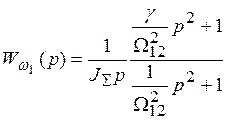.                                  (3-7)

Полученные передаточные функции позволяют представить механическую часть электропривода как объект управления в виде трех звеньев, показанных на рис. 3-3.

Рис. 3-3

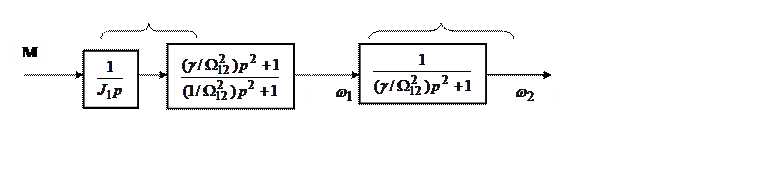
С помощью этой схемы нетрудно записать и передаточную функцию системы по управляющему воздействию при выходной переменной :

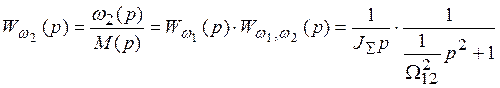.           (3-8)

Передаточной функции (3-8) соответствует структурная схема, рис. 3-4.

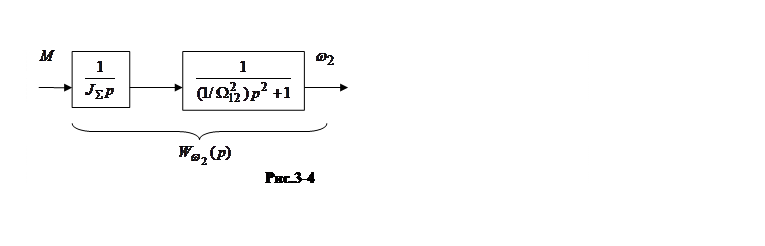
Для анализа свойств системы воспользуемся методом частотных характеристик, для чего запишем выражение частотной характеристики для двухмассовой модели механической системы

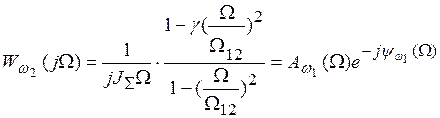,                        (3-9)

где - амплитудно-частотная характеристика (АЧХ),

- фазочастотная характеристика (ФЧХ) при выходной переменной .

Необходимо обратить внимание на то, что при анализе механической и электрической частей системы электропривода здесь и в дальнейшем рассматриваются их передаточные функции, в которых выходная и входная величины чаще всего имеют различные единицы измерения. В этом случае представляет собой не комплексный коэффициент усиления, а комплексный коэффициент передачи, имеющий определенную единицу измерения. В выражении (3-9) его размерность , такую же размерность имеет величина