Основные положения. Упрощенная функциональная схема электромеханической системы. Дискретное преобразование информации, страница 5

Вывод. При реализации импульсных систем не слишком важна форма модулирующего импульса. Но практически наиболее просто реализовать (в математической модели и в реальной установке) прямоугольный импульс. Поэтому и в теории ДСАУ, в качестве основного модулирующего импульса принимают прямоугольный, хотя возможны и другие варианты.

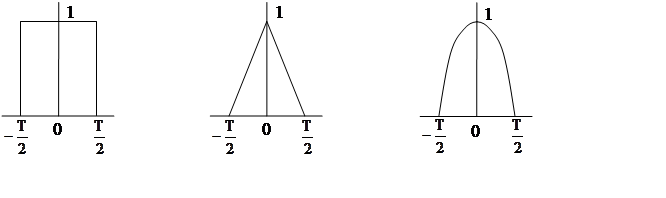
1) Прямоугольная           2) Треугольная                  3) Косинусная

                                     Рис.7. В.

В. 5. Виды модуляции, используемые в импульсных системах

1) Модуляция с изменением амплитуды импульса (АИМ) (см. Рис.8. В.)

При этом виде модуляции выходной сигнал имеет форму такого же импульса, с теми же временными параметрами, но измененного по амплитуде

                                                   

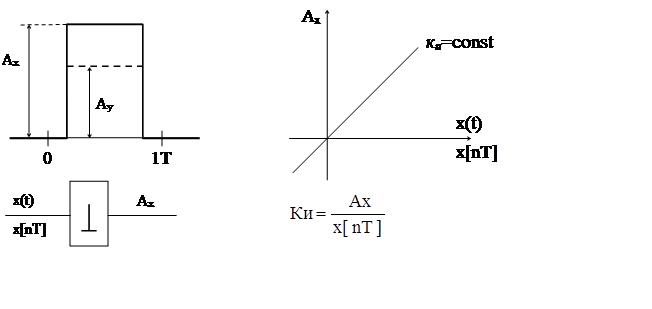
Рис.8. В

В силу такой характеристики коэффициента передачи (коэффициента крутизны) модулятора к_и, амплитудно-импульсную модуляцию (АИМ) называют линейной. Чаще всего к_и =1.

2) Модуляция с изменением ширины импульса (ШИМ) (см. Рис. 9.В.)

 - коэффициент крутизны импульса (каппа),

- относительная продолжительность импульса.

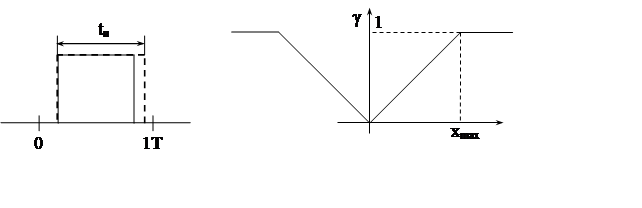
Рис.9.В

Преобразование информации с помощью ШИМ является нелинейным. На графике видно, что ШИМ обладает статической четно - симметричной нелинейностью, если использовать однополярные импульсы. В реальных импульсных устройствах с ШИМ, кроме статической, присутствует еще и динамическая нелинейность. Например, усилители мощности, используемые в регулируемых электроприводах постоянного тока (широтно-импульсные преобразователи), имеют оба вида нелинейностей.

Рассмотрим еще 2-х полярную ШИМ (рис. 10. В). В этом устройстве на протяжении одного интервала квантования Т формируются два импульса t_и1 и t_и2 противоположной полярности. Статическую характеристику устройства

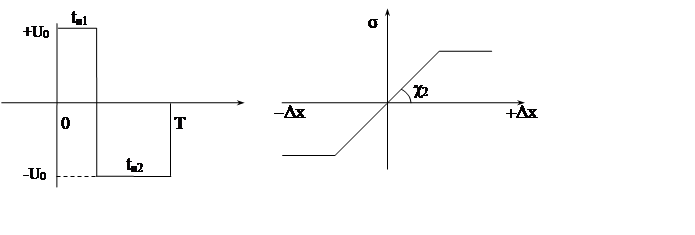
Рис.10. В.

можно рассчитать следующим образом.

Среднее значение входного сигнала преобразователя на интервале Т будет:

Dx=x₁-x₂; где x₁  и x₂ значения входных сигналов, формирующих выходные сигналы преобразователя с амплитудой +U₀ и - U₀ длительностью t_и1 и t_и2.

Коэффициент крутизны двухполярного модулятора χ₂  определим аналогичным образом, учтя, что  и .

Тогда

χ₂, где σ =2γ₁-1.

Двухполярную модуляцию следует применять в ДСАУ с широким диапазоном регулирования выходной координаты (например, скорости  электропривода ω). Поясним это.

Примем во внимание, что невозможно технически сделать электронное устройство (преобразователь напряжения в ширину импульса) без относительной зоны нечувствительности. Поэтому при однополярной ШИМ можно получить γ_max=(0,980,99)≈1 и γ_min=(0,020,01)≈0. Соответственно максимальное напряжение преобразователя пропорционально  и  пропорционально . Поэтому диапазон регулирования  скорости "d" получим не более .

При двухполярной модуляции  при , поэтому диапазон регулирования в таких преобразователях d. Кроме того, модулятор приобретает нечетно - симметричную статическую характеристику.

3) Фазоимпульсная модуляция (время импульсная модуляция) (ФИМ, ВИМ). Коэффициент крутизны таких модуляторов вычисляется по формуле:

χ . Здесь меняется только фаза импульса (см. Рис. 11. В).

          Часто используют еще частотно - импульсную модуляцию (ЧИМ).

Модуляцию различают еще и по роду.

При модуляции первого рода модулятор воспроизводит на выходе значение входного сигнала в моменты квантования (АИМ - I, ШИМ - I и т.д.)                               

Рис. 11. В.

При модуляции второго рода модулятор воспроизводит на выходе значение и форму  сигнала в период квантования (АИМ - II, ШИМ - II и т.д.). Но такие модуляторы используют сравнительно редко.

Скорректировано 08 и 11 02.09. Скорректировано 14.02.10 и 04.04.2011, 12.01.12