Интервальные оценки с доверительной вероятностью. Закон распределения и выбор подходящего методом проб

Часть 1

В результате измерений получена выборка x1, x2, …, xN из генеральной совокупности с неизвестным законом распределения. Выборочные значения расположены в файлах (для каждой групп свой каталог, для каждого варианта файл с названием Distribtuion i), где i – номер варианта.

Число значений N, а также сам массив выборочных значений записаны в файлеи отделены друг от друга пробелами. В случае дискретного распределения значения целые, в случае непрерывного – вещественные.

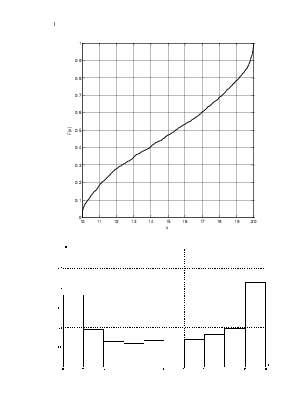
1. Построить:

1.1. Выборочную функцию распределения F(x) (она должна быть ступенчатой!!!)

1.2. Гистограмму

2. Вычислить:

2.1. Точечные оценки:

2.1.1. моментов

·  первого начального,

·  центральных моментов: второго, третьего, четвертого по выборочной функции распределения.

Для оценки первого начального момента использовать среднее арифметическое, выборочную медиану, средину размаха. Определить моду.

2.1.2. асимметрии и эксцесса;

2.1.3. границ интерквантильного промежутка для P=0.95 только по полной выборке; 2.1.4. характеристики по пп. 2.1.1-2.1.2 по отдельным частям выборки, содержащим по N/10 значений (всего 10 частичных выборок). (!!!! Подвыборки должны быть взяты из неотсортированной изначальной выборки)

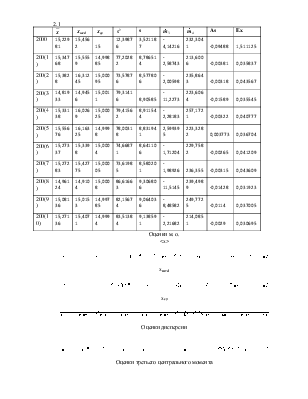
Результаты представить в таблице следующей формы.

Представить эти же результаты графически точками на осях с указанием масштаба на этих осях по форме:

2.2. Интервальные оценки с доверительной вероятностью Q=0.8:

·  первого начального и второго центрального моментов (вычисления выполнить по полной выборке и по отдельным частям, как в п. 2.1.4 - по N/10 значений в каждой частичной выборке).

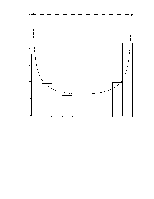
·  интерквантильного промежутка J для P=0.95:

o  по всей выборке с помощью непараметрических толерантных пределов, симметричных и несимметричных относительно среднего арифметического

o  по частичным выборкам с помощью параметрических толерантных пределов, считая закон распределения генеральной совокупности нормальным.

Результаты представить только графически аналогично тому, как описано выше – под графическим представлением соответствующей точечной оценки, предусмотрев для каждого варианта расчета отдельную ось.

Графическое представление толерантных пределов — также на отдельных осях для каждого варианта. Все оси обозначить.

3. Идентифицировать закон распределения и выбрать подходящий методом проб, определяя параметры закона (если моменты параметрами не являются) и проверяя для КАЖДОЙ пробы гипотезу о соответствии предполагаемого закона распределения экспериментальным данным с помощью ТРЕХ критериев:

"хи-квадрат",     Колмогорова-Смирнова,     "омега-квадрат".

Для начальной ориентировки в выборе закона использовать вид гистограммы, соотношения между моментами и полученные значения эксцесса и асимметрии. Многие теоретические сведения можно найти в интернете по адресу