










этом знаменатель
передаточной функции будет преобразован к виду: 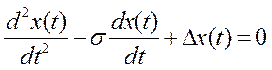 . (3)
. (3)
В
зависимости от соотношения ![]() корни
характеристического уравнения передаточной функции могут быть комплексными,
вещественными, правыми, левыми… Следовательно, кривая
корни
характеристического уравнения передаточной функции могут быть комплексными,
вещественными, правыми, левыми… Следовательно, кривая ![]() есть граница, отделяющая комплексные
корни от вещественных. Изобразим эту границу:
есть граница, отделяющая комплексные
корни от вещественных. Изобразим эту границу:
|
|
Тогда выделяются следующие области: Область Область Область Область Область В каждой из этих областей будет свое движение системы |
Дифференциальное уравнение второго порядка (1) соответствует системе уравнений первого порядка вида:
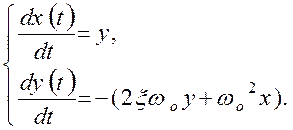
И для этой систему уравнение фазовой траектории будет иметь вид:
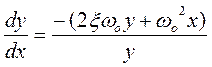 или
или 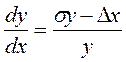 . (4)
. (4)
Изучим влияние ![]() и
и ![]() на решение дифференциального
уравнения.
на решение дифференциального
уравнения.
Система без вязкого трения
Рассмотрим случай системы без вязкого трения, когда ![]()
![]() . Уравнение траектории (4) будет
приведено к виду
. Уравнение траектории (4) будет
приведено к виду 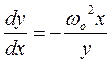
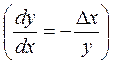 , (5)
, (5)
а дифференциальное уравнение (1) также преобразуется:
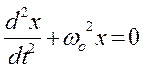 или
или
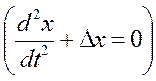 .
.
Изоклины (линии равных углов наклона касательных к
фазовой траектории 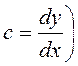 будут
определены уравнением
будут
определены уравнением ![]() или
или ![]() . При
. При ![]() угол наклона касательных к
траектории составляет
угол наклона касательных к
траектории составляет ![]() , а при
, а при ![]() угол равен
угол равен ![]() (фазовая траектория пересекает
оси OX и OY
под прямым углом).
(фазовая траектория пересекает
оси OX и OY
под прямым углом).
|
|
Решением уравнения (5) будет эллипс При этом решение исходной системы при |
Движение автономной системы при 0<ξ<+1
Корни характеристического уравнения при таких
параметрах будут комплексными с отрицательной вещественной частью. Движение ![]() будет колебательным и
затухающим.
будет колебательным и
затухающим.
Уравнение изоклины в этом случае имеет вид:
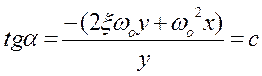
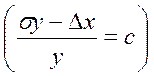 , откуда
, откуда 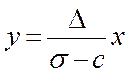 .
.
|
|
Полагая
|
Уравнение движения системы является колебательным с затуханием:
![]() ,
, ![]() .
.
Фазовая траектория имеет вид спирали, закручивающейся по часовой стрелке в начало координат – это состояние покоя (устойчивого равновесия).
Движение автономной системы при 0>ξ>-1
В этом случае все выкладки аналогичны предыдущим.
|
|
Уравнение прямой Так как движение расходящееся, то центр (.) – неустойчивый фокус. |
Движение автономной системы при ξ>+1
Корни характеристического уравнения являются
отрицательными вещественными: ![]() . Движение
системы – асимптотически устойчиво и определяется соответствующими экспонентами:
. Движение
системы – асимптотически устойчиво и определяется соответствующими экспонентами:
![]()
![]() .
.
Изоклины фазовой траектории, как и ранее, имеют вид 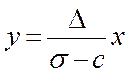 . В дополнение к ним появляется
еще одна изоклина, соответствующая конечному
. В дополнение к ним появляется
еще одна изоклина, соответствующая конечному ![]() движению системы. При этом выполняется
движению системы. При этом выполняется
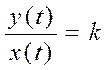 (так как
(так как ![]() убывает быстрее, чем
убывает быстрее, чем ![]() ), причем
), причем 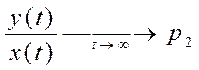 . То есть
. То есть ![]() .
.
|
|
Тогда
из общего уравнения изоклины |
Движение автономной системы при ξ<-1
|
|
Решение
системы в этом случае Точка (.) – неустойчивый узел. |
Движение автономной системы при ω²<0
Рассмотрим область ![]() . Дифференциальное уравнение,
соответствующее этой области, имеет вид:
. Дифференциальное уравнение,
соответствующее этой области, имеет вид: 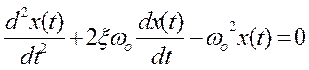 .
.
|
|
Корни
его характеристического уравнения будут вещественными, но разных знаков: Фазовая траектория имеет форму гиперболы. Фазовый портрет – седло. |
Точка (.) – точка неустойчивого равновесия.
Расчет переходных процессов по фазовой траектории
Рассмотрим
некоторую фазовую траекторию. Пусть начальная точка на ней: ![]() и некоторое
и некоторое ![]() . Возьмем небольшое приращение х,
то есть ∆х. Вообразим, что ∆х задано как
. Возьмем небольшое приращение х,
то есть ∆х. Вообразим, что ∆х задано как ![]() . Тогда
. Тогда ![]() - это скорость.
- это скорость.
|
|
Полагая,
что |
|
Если правая часть дифференциального уравнения не дифференцируемая функция (релейная система), то особые точки могут сливаться в целые линии – линии переключения, и по разные стороны от них нелинейный элемент НЭ системы переключается в разные состояния.
Рассмотрим нелинейную следящую систему с гистерезисом:
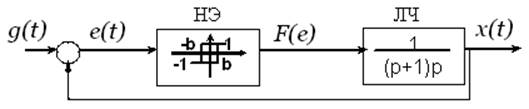
Свободные движения этой системы (при g(t)=0) описываются нелинейным дифференциальным уравнением второго порядка:
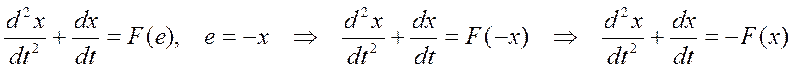 , которое преобразуется к системе
двух уравнений первого порядка:
, которое преобразуется к системе
двух уравнений первого порядка:
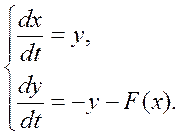
Уравнение фазовой траектории для этой системы будет иметь вид:
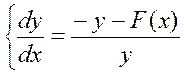 .
.
Основная идея: там, где нелинейный элемент находится в одном из своих устойчивых состояний, дифференциальное уравнение сильно упрощается и его решают отдельно в каждой из этих областей и на границе линии переключения.
1)
Область N1: F(x)
= –1 при условии: 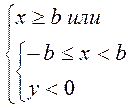 .
.
Система
уравнений упрощается: 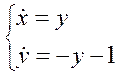 ;
уравнение фазовых траекторий:
;
уравнение фазовых траекторий: 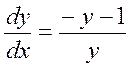 ,
решение которого имеет вид:
,
решение которого имеет вид: ![]() .
.
В соответствии с этим уравнением строится фазовая траектория системы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.