1 вопрос: Метрические характеристики графовых моделей сетей и аксиомы Фреше.
Граф называется взвешенным если его вершинам или ребрам приписаны числовые характеристики (веса).
Граф связен тогда и только тогда , когда любая пара его вершин связаны маршрутом.
Задан взвешенный связный граф G :
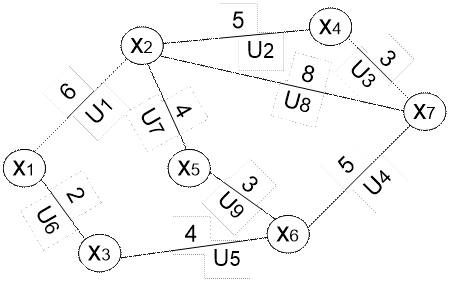
Рис.1 Граф G
Составим для заданного графа матрицу смежности.
Две вершины называются смежными в графе тогда и только тогда , когда существует ребро графа инцидентное (принадлежащее) им обоим .
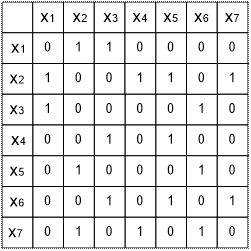
Рис.1 Матрица смежности графа G
Цифра 1 на пересечении строки и столбца таблицы обозначает смежность этих вершин, а цифра 0 – говорит о том, что эти две вершины не смежны между собой.
Теперь составим матрицу инцидентности.
Вершина Х и ребро U
называются инцидентными если ![]() , т.е. ребро U принадле-жит этим двум ребрам.
, т.е. ребро U принадле-жит этим двум ребрам.
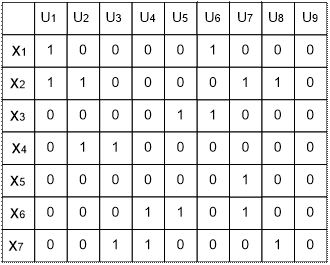
Рис.2 Матрица инцидентности графа G
Теперь составим матрицу расстояний графа G.
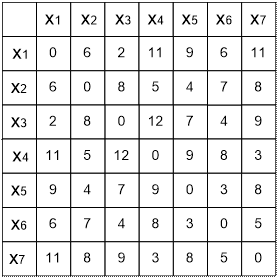
Рис.2 Матрица расстояний графа G
Зная расстояния от вершины к вершине, можем найти эксцентриситеты графа G.
Эксцентриситетом вершины в графовой модели сети называется максимальное из расстоя-ний от вершины Х до других вершин графа.

Рис. 3 Эксцентриситеты графа G
Радиус графа – это минимальное из эксцентриситетов вершин графа .
Диаметр графа – это максимальное из эксцентриситетов вершин графа.
Согласно этим определениям и результатам таблицы на рис.3 определяем радиус и диаметр гра- фа G . Радиусом графа являются вершины х2 и х6 , а его диаметрами х3 и х4 .
Центр (центральная вершина) графа – это вершина, эксцентриситет которой равен радиусу.
Периферийная вершина – это вершина, эксцентриситет которой равен диаметру графа.
Значит, в заданном графе G центрами будут вершины х2 и х6 , а его периферийными вершинами будут вершины х3 и х4.
Аксиомы Фреше
Рассмотрим их на простом примере.
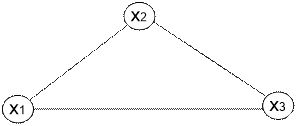
1) Аксиома рефлексивности :
![]() , т.е.
расстояние от х1 до х1 равно 0 (замкнута на саму себя).
, т.е.
расстояние от х1 до х1 равно 0 (замкнута на саму себя).
2) Аксиома симметричности :
![]() ,т.е.расстояние
от вершины х1 до вершины х2 равно расстоянию от вершины
х2 до вершины х1.
,т.е.расстояние
от вершины х1 до вершины х2 равно расстоянию от вершины
х2 до вершины х1.
3) Аксиома транзитивности :
![]()
![]()
![]()
![]()
2 вопрос:Алгоритм Прима-Краскала. Его применение при оптимизации проектных решений
Одной из важнейших задач , возникающих при проектировании сетей связи – определение кратчайших путей между всеми парами узлов сети. Предполагается что существует несколько вариантов путей соединяющих пару вершин, а выбран один из них – кратчайший
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.