Колебания атомов кристаллической решетки. Одномерные колебания упругой струны. Дисперсионная зависимость для непрерывной струны

обычное волновое уравнение для упругих волн, распространяющихся вдоль струны. Решение этого уравнения будем искать в виде бегущей продольной монохроматической волны:

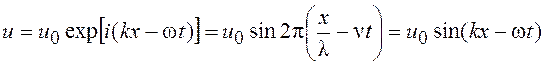,            (2.5)

где  – амплитуда колебания;  – частота колебаний;  – круговая частота;  – время;  – длина волны:  – волновое число. После подстановки решения (2.5) в уравнение (2.4) получим дисперсионное соотношение

.                                            (2.6)

Из (2.6) следует, что для упругой волны, распространяющейся в неограниченно протяженной струне, частота колебаний линейно зависит от волнового числа (рис. 2.2).

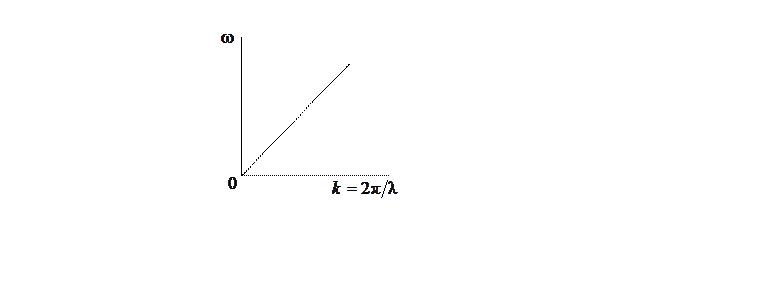
Рис. 2.2. Дисперсионная зависимость для непрерывной струны

При этом скорость распространения волны  для данного материала –  величина постоянная, поскольку  и  являются характеристиками только материала. Так, для железной струны (, ) имеем .

Как видно из рис. 2.2, модуль волнового числа может меняться от  до , а следовательно, частота колебаний меняется непрерывно от  до .

2.2. Упругие волны в монокристаллах

Процессы распространения упругих волн в кристаллах много сложнее процессов распространения электромагнитных волн. Электромагнитные волны всегда поперечны, упругие (звуковые) волны могут быть поперечными и продольными. Продольные волны – волны сжатий и растяжений, поперечные – волны деформации сдвига. В каждом заданном направлении в кристалле распространяются в общем случае три поляризованные упругие волны с разными скоростями.

Рассмотрим распространение упругих волн в кристалле, плотность которого , внутри кристалла выберем элементарный параллелепипед с ребрами , параллельными кристаллографическим осям координат . Как и в случае упругой струны, при движении упругой волны по кристаллу каждая грань элементарного параллелепипеда под действием напряжения  совершает небольшое перемещение (в области упругости, когда справедлив закон Гука). Найдем уравнение движения для поступательного перемещения элементарного параллелепипеда при распространении упругой волны вдоль направления  (рис. 2.3).

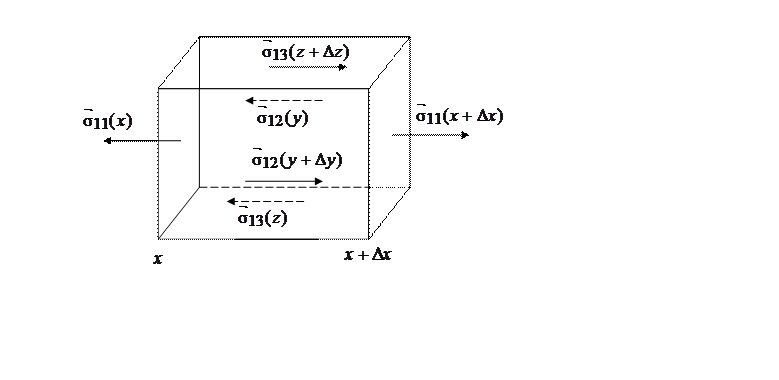
Рис. 2.3. Силы, действующие на элементарный параллелепипед

при движении упругой волны в направлении оси

На грань  действует напряжение , а на параллельную ей грань  - напряжение . Результирующая сила, действующая в направлении , равна 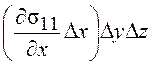. Другие силы, действующие в направлении , вызваны изменением внутри параллелепипеда напряжений  и , так что в направлении  результирующая сила

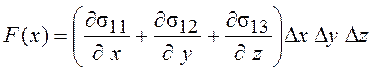.                         (2.7)

Обозначим  компоненты вектора смещения центра масс параллелепипеда. Сила, согласно второму закону Ньютона, равна массе параллелепипеда , умноженной на  – компоненту ускорения . Уравнение движения параллелепипеда в направлении  под действием напряжений, принимает вид

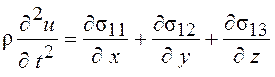.                                     (2.8)

Если смещение  обозначить через , где  и  соответствует , , то возможные уравнения движения можно записать в виде

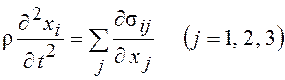,                                   (2.9)

где  – компоненты тензора напряжений.

Найдем решение уравнений движения для плоских волн, распространяющихся в направлении [100] для кубического кристалла. Решение с учетом упругих постоянных для данной ориентации будем искать в виде продольной волны

.                                          (2.10)

Здесь  – амплитуда колебаний;  – волновой вектор.

Волновой вектор  и смещение  направлены вдоль ребра куба и совпадают по направлению с осью , т.е. вектор направлен по нормали к фронту волны.

После соответствующих преобразований получим

,                                          (2.11)

где  – скорость распространения продольной упругой (звуковой) волны в направлении [100].

Другим решением будет поперечная волна или волна сдвига, с волновым вектором, направленным вдоль ребра куба, совпадающим по направлению с осью , смещение же  происходит по направлению оси :

.                                            (2.12)

После преобразований для смещения v получим

,                                              (2.13)

где  – скорость распространения поперечной упругой волны в направлении [100].

Наконец, третье решение – это также волна сдвига с волновым вектором, направленным вдоль ребра куба, совпадающим по направлению с осью , но смещение  происходит по направлению :

.                                            (2.14)

После преобразований для смещения  получим

.                                                   (2.15)

Таким образом, для одного и того же волнового вектора  параллельного направлению [100] возникают три упругие волны – одна продольная и две поперечные. При этом две независимые волны сдвига имеют одинаковые скорости. В случае произвольного направления вектора  имеют место три поляризованные волны, распространяющиеся с разными скоростями, которые не зависят от частоты колебаний. Как видно из выражений для скоростей, чем меньше плотность