Макет тензорезистивного измерительного преобразователя силы в напряжение. Калибровка одиночных тензорезисторов на образцовой пластине с оценкой характеристик погрешности результатов калибровки

1. Цель работы.

Практическое ознакомление:

·  с устройством, методами испытаний и применением тензорезисторов для измерения механических упругих деформаций механических конструкций,

·  с методикой калибровки тензорезистивных преобразователей,

·  с принципами построения и методами калибровки тензорезистивных измерительных преобразователей деформации и силы в напряжение и цифровой код.

2. Объекты исследования.

·  Тензорезисторы.

·  Четырехканальный тензорезистивный измерительный преобразователь деформации в напряжение.

·  Макет тензорезистивного измерительного преобразователя силы в напряжение.

3. Использованные средства измерений.

Таблица 3.1. Перечень использованных средств измерений

№ п/п	Наименование средства измерений	Тип средства измерений	Измеряемая величина	Предел измерений (конечное значение)	Собственное сопротивление	Предел допускаемой основной погрешности
1	Универсальный мост	Е7-10	Сопротивление	0÷1000 Ом	-	0,01 Ом

4. Программа работы.

4.1. Калибровка одиночных тензорезисторов на образцовой пластине с оценкой характеристик погрешности результатов калибровки.

4.2. Калибровка макета тензорезистивного преобразователя силы в напряжение.

4.3. Измерение деформации консольной балки.

5. Выполнение работы.

5.1. Пункт 4.1 программы работы.

Исходные данные:

1. Тензорезисторы № 5 и № 2.

2. Расстояние от точки приложения прогибающего воздействия до места закрепления пластины: H = (200 ± 1) мм,

3. Толщина пластины: h = (1 ± 0,1) мм,

4. Количество циклов измерений: k = 6.

Расчет теоретических значений деформаций ε_i для тензорезисторов при значениях прогибов, равных соответственно, Δf_i = 5, 10, 15, 20, 25 мм.

Таблица 5.1.1. Теоретические значения деформаций ε_i

Δfi, мм	5	10	15	20	25
εi	0,025	0,05	0,075	0,1	0,125

Пример расчетов:

Тензорезистор № 5.

f₀ = 20 мм.

Таблица 5.1.2. Значения сопротивления тензорезистора.

Перемещ. винта fi, мм	Прогиб Δfi, мм	Ri	Сопротивление тензорезистора, Ом
			1	2	3	4	5	6
20	0	R0	425,72	425,68	425,79	425,73	425,71	425,71
25	5	R1	425,80	425,78	425,98	425,80	425,81	425,47
30	10	R2	425,86	425,87	426,10	425,90	425,88	425,87
35	15	R3	425,96	425,95	426,19	426,20	426,00	425,94
40	20	R4	426,39	426,27	426,42	426,36	426,20	426,22
45	25	R5	426,40	426,40	426,45	426,45	426,31	426,31

Таблица 5.1.3

i	Прогиб Δfi, мм	Деформация εi	Относительное изменение сопротивления тензорезистора						Средние арифм. значения	Среднеквадр. знач. si
0	0	0	-0,000007	-0,000101	0,000157	0,000016	-0,000031	-0,000031	0,00000078	0,000086
1	5	0,025	0,000181	0,000134	0,000604	0,000181	0,000204	-0,000594	0,000118	0,000390
2	10	0,050	0,000322	0,000345	0,000886	0,000416	0,000369	0,000345	0,000447	0,000217
3	15	0,075	0,000557	0,000533	0,001097	0,001120	0,000651	0,000510	0,000745	0,000286
4	20	0,100	0,001567	0,001285	0,001637	0,001496	0,001120	0,001167	0,001379	0,000217
5	25	0,125	0,001590	0,001590	0,001708	0,001708	0,001379	0,001379	0,001559	0,000149

Примеры расчетов.

Относительные изменения сопротивлений тензорезистора:

Средние арифметические значения этих величин:

Среднеквадратические отклонения:

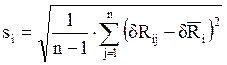
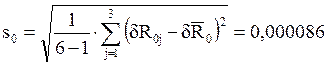
Проверка гипотезы о равноточности измерений по критерию Кочрена:

Таблица 5.1.4. Значения дисперсий.

i	Дисперсия si2*10-8
0	0,7430
1	15,177
2	4,7156
3	8,1880
4	4,7230
5	2,2217

g(α, k, n) = g(0.05, 6, 6) = 0.4447

Как видно, G < g, следовательно, гипотеза верна, наши измерения равноточные.

Рассчитаем коэффициент тензочувствительности:

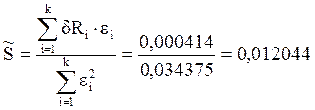
И среднеквадратическое отклонение:

 

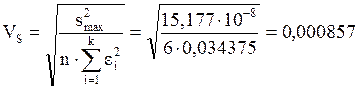
Тензорезистор № 2.

f₀ = 20 мм.

Таблица 5.1.3. Значения сопротивления тензорезистора.

Перемещ. винта fi, мм	Прогиб Δfi, мм	Ri	Сопротивление тензорезистора, Ом
			1	2	3	4	5	6
20	0	R0	426,30	426,29	426,30	426,31	426,30	426,32
25	5	R1	426,19	426,27	426,20	426,16	426,23	426,16
30	10	R2	425,98	425,96	425,97	425,97	425,97	425,99
35	15	R3	425,82	425,82	425,81	425,83	425,81	425,81
40	20	R4	425,69	425,69	425,78	425,68	425,68	425,70
45	25	R5	425,58	425,58	425,56	425,56	425,56	425,56

Таблица 5.1.3

i	Прогиб Δfi, мм	Деформация εi	Относительное изменение сопротивления тензорезистора						Средние арифм. значения	Среднеквадр. знач. si*10-5
0	0	0	-0,0000077	-0,0000311	-0,0000077	0,0000157	-0,0000077	0,0000391	0,00000078	2,42268
1	5	0,025	-0,0002658	-0,0000781	-0,0002423	-0,0003361	-0,0001719	-0,0003362	-0,00023840	9,99813
2	10	0,050	-0,0007584	-0,0008053	-0,0007818	-0,0007818	-0,0007818	-0,0007349	-0,00077402	2,42268
3	15	0,075	-0,0011337	-0,0011337	-0,0011572	-0,0011102	-0,0011572	-0,0011571	-0,00114152	1,91530
4	20	0,100	-0,0014387	-0,0014387	-0,0012275	-0,0014621	-0,0014621	-0,0014152	-0,00140737	8,98353
5	25	0,125	-0,0016967	-0,0016967	-0,0017436	-0,0017436	-0,0017436	-0,0017436	-0,00172796	2,42268

Примеры расчетов:

Относительные изменения сопротивлений тензорезистора:

Средние арифметические значения этих величин:

Среднеквадратические отклонения:

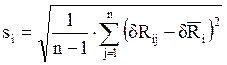
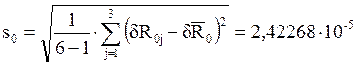
Проверка гипотезы о равноточности измерений по критерию Кочрена:

Таблица 5.1.4. Значения дисперсий.

i	Дисперсия si2*10-10
0	5,86937
1	99,9963
2	5,86937
3	3,66835
4	80,0704
5	5,86937

g(α, k, n) = g(0.05, 6, 6) = 0.4447

Как видно, G > g, следовательно, гипотеза отклоняется, и наши измерения незначительно изменяются.

Рассчитаем коэффициент тензочувствительности:

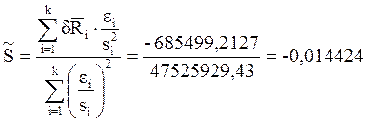
И среднеквадратическое отклонение:

 

 

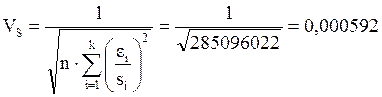
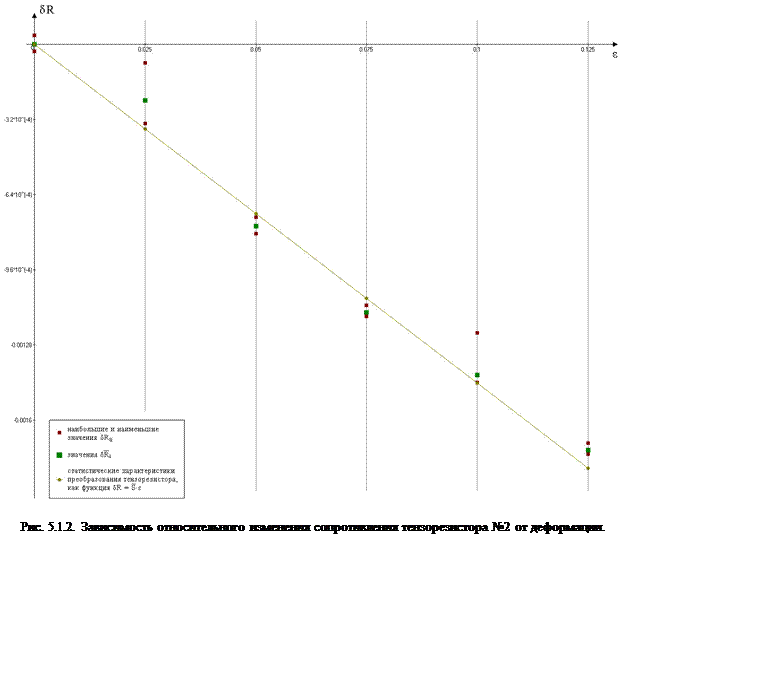5.2. Пункт 4.2 программы работы.

Исходные данные:

1. Каналы № 2 и № 3.

2. Количество измерений в каждой точке: n = 6.

Канал № 2.

Таблица 5.2.1. Экспериментальные данные.

Сила F, Н	Среднее арифметическое значение Ū, В	Дисперсия si2, В
0	-0,004667	0,000137
5	1,320333	0,000227
10	2,675333	0,000257
15	3,965333	0,000257
15	3,993666	0,000147
10	2,695333	0,000417
5	1,335333	0,000177
0	0,005333	0,000377

Проверка гипотезы о равноточности измерений.

g(α, k, n) = g(0.05, 8, 6) < 0,3974

G < g, следовательно гипотеза о равноточности измерений верна.

Коэффициент преобразования:

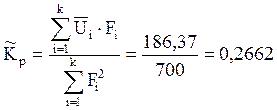
Среднеквадратическое значение:

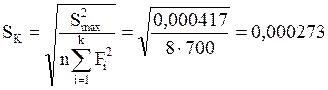
Таблица 5.2.2.

Сила F, Н	Характеристика преобразования U датчика силы, В	Среднее арифметическое значение Ū, В	Среднеквадратическое значение si, В	Параметрические толерантные пределы siк(n,P,Q), В
0	0	-0,004667	0,011704700	0,043681940
5	1,331	1,320333	0,015066519	0,056228250
10	2,662	2,675333	0,016031220	0,059828511
15	3,993	3,965333	0,016031220	0,059828511
15	3,993	3,993666	0,012124356	0,045248095
10	2,662	2,695333	0,020420578	0,076209597
5	1,331	1,335333	0,013304135	0,049651031
0	0	0,005333	0,019416488	0,072462333

Пример расчетов:

Определим границы интервала (– Δ_слК, +Δ_слК) для случайной составляющей абсолютной погрешности коэффициента преобразования.

Границы интервала неопределенности значения систематической составляющей абсолютной погрешности (– Δ_сК, +Δ_сК) вычисляются по формуле:

Границы интервала (– ΔК, +ΔК), содержащего с вероятностью P значения общей погрешности определения коэффициента преобразования, определяется суммой:

ΔК = Δ_слК + Δ_сК = 0,00064 + 0,00532 = 0,00596

Коэффициент с двучленной формулы:

Вычислим параметрические толерантные пределы:

Предельное значение абсолютной аддитивной погрешности:

В результате можно определить коэффициент d двучленной формулы:

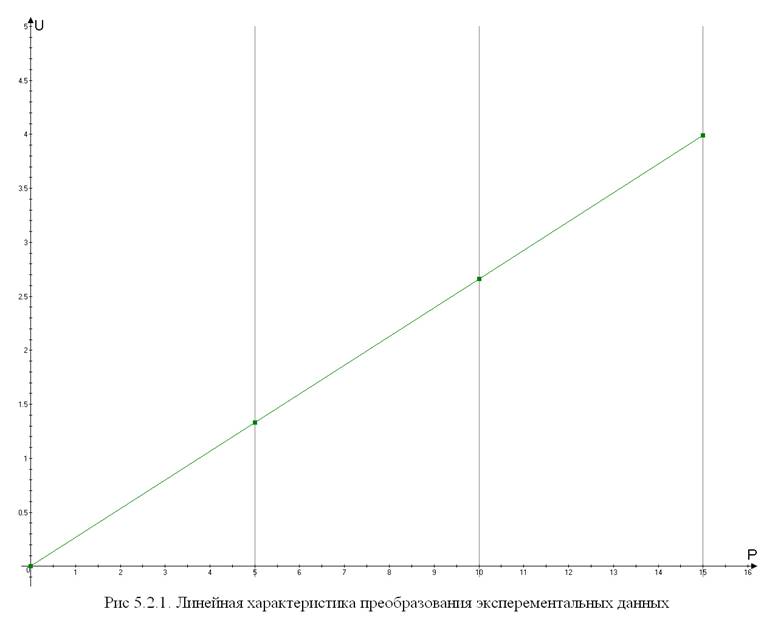
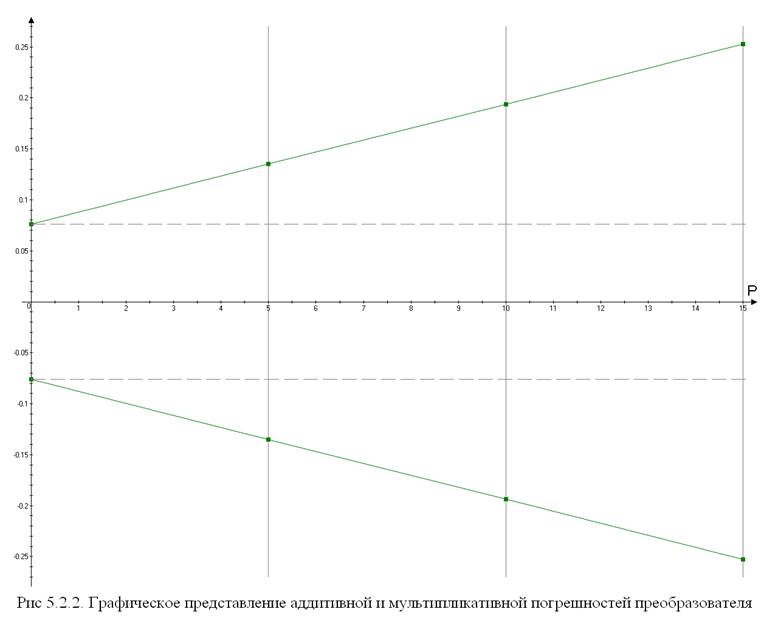
Канал № 3.

Таблица 5.2.3. Экспериментальные данные.

Сила F, Н	Среднее арифметическое значение Ū, В	Дисперсия si2, В
0	-0,000666	0,000297
5	1,072667	0,000057
10	2,166000	0,000270
15	3,224333	0,000107
15	3,251000	0,000200
10	2,197667	0,000387
5	1,101000	0,000280
0	0,014333	0,000147

Проверка гипотезы о равноточности измерений.

g(α, k, n) = g(0.05, 8, 6) < 0,3974

G < g, следовательно гипотеза о равноточности измерений верна.

Коэффициент преобразования:

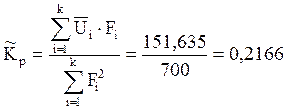
Среднеквадратическое значение:

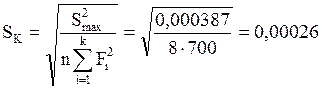
Таблица 5.2.4.

Сила F, Н	Характеристика преобразования U датчика силы, В	Среднее арифметическое значение Ū, В	Среднеквадратическое значение si, В	Параметрические толерантные пределы siк(n,P,Q), В
0	0	-0,000666	0,017233688	0,064316124
5	1,083	1,072667	0,007549834	0,028175980
10	2,166	2,166000	0,016431677	0,061323019
15	3,249	3,224333	0,010344080	0,038604107
15	3,249	3,251000	0,014142136	0,052778452
10	2,166	2,197667	0,019672316	0,073417083
5	1,083	1,101000	0,016733201	0,062448306
0	0	0,014333	0,012124356	0,045248097

Пример расчетов:

Определим границы интервала (– Δ_слК, +Δ_слК) для случайной составляющей абсолютной погрешности коэффициента преобразования.

Границы интервала неопределенности значения систематической составляющей абсолютной погрешности (– Δ_сК, +Δ_сК) вычисляются по формуле:

Границы интервала (– ΔК, +ΔК), содержащего с вероятностью P значения общей погрешности определения коэффициента преобразования, определяется суммой:

ΔК = Δ_слК + Δ_сК = 0,00062 + 0,00532 = 0,00594

Коэффициент с двучленной формулы:

Вычислим параметрические толерантные пределы:

Предельное значение абсолютной аддитивной погрешности:

В результате можно определить коэффициент d двучленной формулы:

 

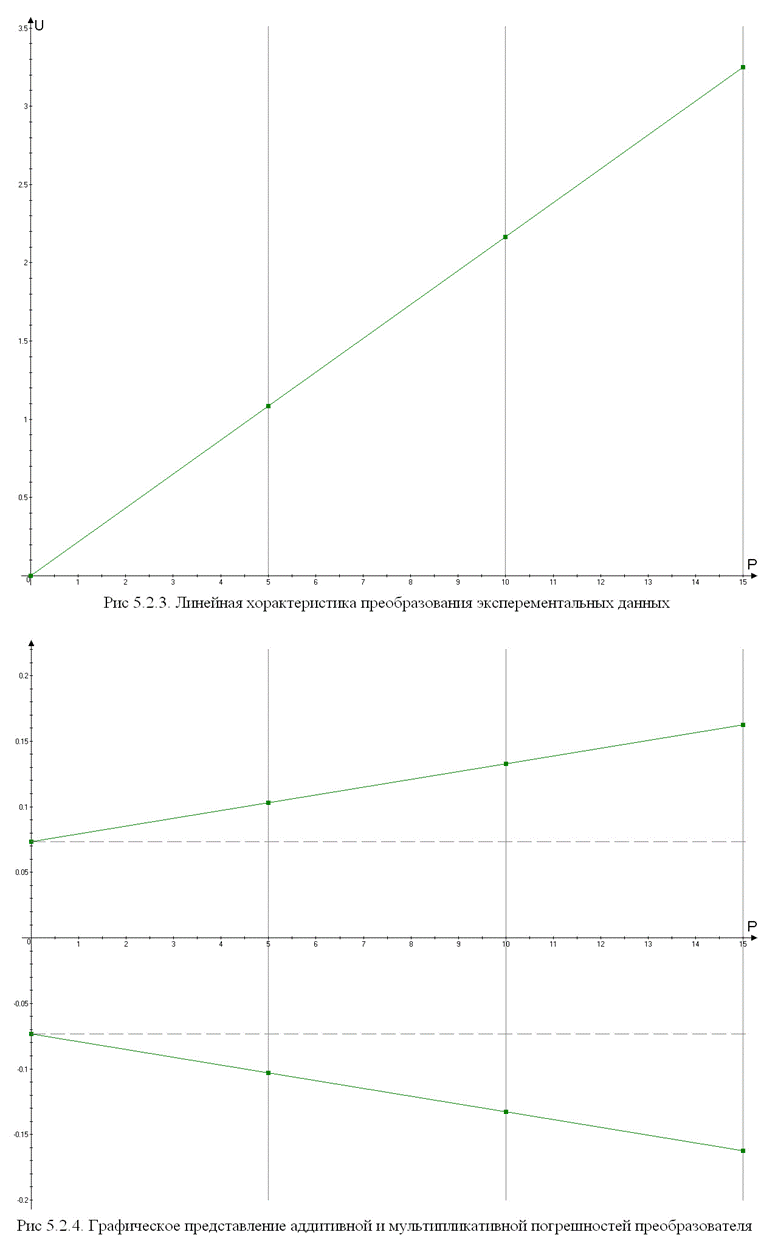
6. Вывод

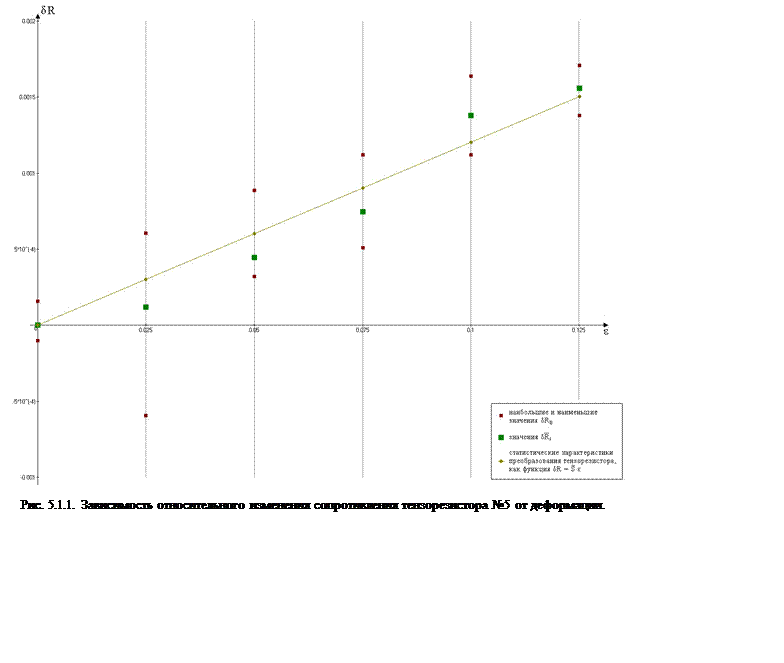
В ходе калибровки тензорезисторов были получены их коэффициенты тензочувствительности, что позволяет их использовать для выполнения измерений деформации. Была произведена оценка их погрешностей, и среднеквадратичное значение случайной погрешности определения коэффициента тензочувствительности транзистора №2 меньше, чем у транзистора №5, а значит он более надежен, и его использование будет приносить достаточно четкие характеристики.

Калибровка каналов №2 и №3 макета преобразователя силы в напряжение показала, что характеристика преобразования каналов практически совпадает. Так же было замечено, что основной вклад в погрешность определения