Измерение параметров электрических цепей на переменном токе. Измерение параметров конденсатора с помощью моста переменного тока, страница 5

Реактивные компоненты электрических цепей (конденсаторы и катушки индуктивности) проявляют себя, как комплексные сопротивления, обладающие кроме реактивной составляющей активным сопротивлением, которое характеризует потери активной энергии и называется сопротивлением потерь. Для учета вклада этого сопротивления в общий импеданс, которым обладают реактивные компоненты, их представляют в виде схем замещения (см. рис 4).

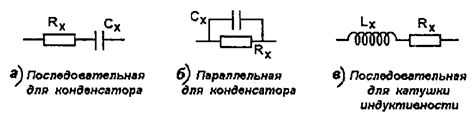
Рис.4 Схемы замещения

Если конденсатор обладает малыми потерями, его схему замещения удобно представить в виде последовательного соединения идеального конденсатора и сопротивления потерь, а импеданс такого соединения выражается формулой

   ,

Конденсатор со значительными потерями описывается параллельной схемой замещения, импеданс и комплексная проводимость которой выражается формулами :

 , где G=1/R

Для катушек индуктивности принята последовательная схема замещения с импедансом :

Активные потери в конденсаторе и катушке индуктивности приводят к тому, что фазовый сдвиг между напряжением и током в реальном реактивном компоненте электрической цепи отличается от π/2 на угол δ. Общепринятой характеристикой потерь конденсаторов является тангенс этого угла: tgδ Для катушек индуктивности характеристикой потерь является добротность, но в ряде случаев и для них используется tgδ .

Для рассмотренных схем замещения tgδ выражается формулами (в порядке их представления):

tgδ=ωRC;   tgδ=1/ωRC=G/ωC;   tgδ=R/ωL=1/ωGL

6.2. Мосты переменного тока

Одним из наиболее эффективных средств измерения параметров электрических цепей являются мосты постоянного и переменного тока, которые широко применяются и в качестве образцовых средств при поверке мер электрических величин. Мосты переменного тока позволяют производить измерения емкости, индуктивности и связанных с ними параметров: тангенса угла потерь конденсаторов, добротности катушек индуктивности, а также активного сопротивления с погрешностью от единиц до тысячных долей процента. Конкретное значение погрешности определяется погрешностью элементов, из которых составлен мост, а также чувствительностью индикатора равновесия моста. Принципиальная схема моста переменного тока может быть представлена в виде эквивалентной схемы, состоящей из четырех комплексных сопротивлений Z₁ - Z₄ (рис. 5).

Источником питания моста переменного тока является генератор синусоидального напряжения Г. Индикатор равновесия моста ИН включен в измерительную диагональ моста. Как известно, ток и напряжение в измерительной диагонали моста равны нулю, если выполняется условие равновесия:

Z₁xZ₃ = Z₂xZ₄.           (1)

Если в одно из плеч моста включено комплексное сопротивление,   значение которого необходимо измерить, например Z₁, то, изменяя сопротивления других плеч, можно добиться отсутствия тока или напряжения в измерительной диагонали и, зная сопротивления плеч Z₂-Z₄, рассчитать значение неизвестного сопротивления. Комплексному условию равновесия моста (1) соответствуют два вещественных равенства, которые получают покомпонентным приравниванием действительных и мнимых частей комплексных сопротивлений Z=R+jX:

                                                                                   (2)

Полагая  имеем

Последнее соотношение можно выразить двумя равенствами :

 ,

Таким образом, мостовые цепи переменного тока в отличие от мостовых цепей постоянного тока, могут быть уравновешены только при одновременном выполнении двух условий равновесия. Для этого необходима регулировка, по крайней мере, двух параметров.

В качестве индикаторов равновесия удобно использовать электроннолучевой осциллограф, который позволяет разделить признаки неуравновешенности моста по амплитуде и по фазе благодаря схеме его включения. Если фазы напряжения питания и напряжения в диагонали моста различны, то на экране осциллографа будет изображаться эллипс, а при равенстве фаз - прямая, наклон которой определяется амплитудой напряжения в диагонали моста: с уменьшением амплитуды наклон прямой уменьшается. По мере приближения к равновесию наклон большой оси эллипса и его малая ось будут уменьшаться, и при достижении равновесия эллипс вырождается в горизонтальную прямую.