ДОПОЛНЕНИЕ. Образуемый контур должен как можно более соответствовать реальной цепи протекания электрического тока.
РЕКОМЕНДАЦИЯ. Во многих случаях в качестве "общей" ветви желательно использовать ветвь, включающую нагрузку.
Итак, в соответствии со II законом Кирхгофа (алгебраическая сумма ЕДС контура равна алгебраической сумме падений напряжений на элементах контура) при обходе обоих контуров схемы рис.7 получают:
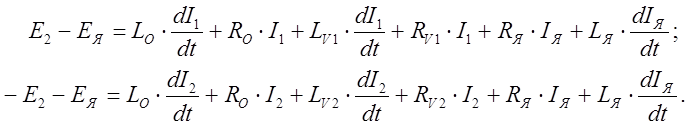 (2)
(2)
В дальнейшем с
целью удобства записи вводится обозначение 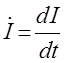 .
.
Итак, получены одно алгебраическое уравнение (1) и два дифференциальных уравнения (2), описывающих процессы, происходящие в управляемом выпрямителе, схема которого изображена на рис.1 (рис.7).
ТРЕТИЙ ЭТАП моделирования необходим для приведения математической модели управляемого выпрямителя (1), (2) к виду, удобному для решения поставленной задачи. Таким видом может быть система дифференциальных уравнений первого порядка в форме Коши.
Для этого первоначально в системе уравнений (2) переносят члены с производными токов в левую часть уравнений, а оставшиеся члены - в правую. В результате этой операции получают:
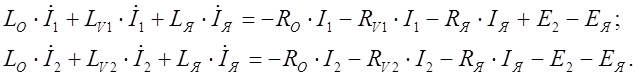 (3)
(3)
В системе (3), состоящей из двух уравнений, имеются три переменных (I1, I2 и IЯ). То есть одна переменная является "лишней" и подлежит исключению с учетом уравнения (1). Для выбора исключаемой переменной (или переменных, которые будут оставлены в уравнениях) целесообразно руководствоваться правилом:
ПРАВИЛО 3. В качестве переменных, удовлетворяющих системе дифференциальных уравнений (3), должны быть переменные, являющиеся токами, протекающими через элементы, параметры которых меняются в зависимости от значения этих токов.
Такими элементами в нашем случае являются тиристоры. Следовательно, "лишняя" переменная в (3) - это ток IЯ. Тогда из (1) следует:
IЯ =I1+ I2. (4)
После подстановки (4) в (3) и приведения подобных членов система дифференциальных уравнений принимает вид:
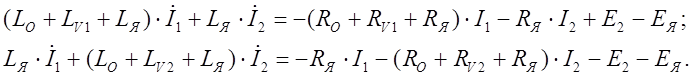 (5)
(5)
или в матричной форме:
![]() , (6)
, (6)
где использованы обозначения:
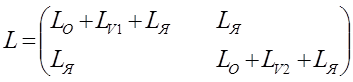 - матрица размерности 2х2;
- матрица размерности 2х2;
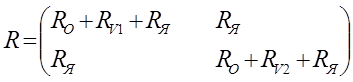 - матрица размерности 2х2;
- матрица размерности 2х2;
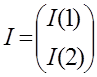 - вектор переменных состояния
размерности 2, причем
- вектор переменных состояния
размерности 2, причем
![]() ;
;
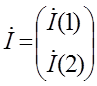 - вектор производных состояния
размерности 2, причем
- вектор производных состояния
размерности 2, причем
![]() ;
;
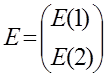 - вектор возмущений размерности 2,
причем
- вектор возмущений размерности 2,
причем
![]() .
.
Для получения системы дифференциальных уравнений в форме Коши необходимо выразить из (6) (либо (5)) производные для каждого из токов. То есть требуется привести систему (6) к виду
![]() , (7)
, (7)
где, если использовать аппарат векторно-матричного исчисления,
![]() ,
, ![]() ,
а
,
а ![]() . (8)
. (8)
Эта операция в рассматриваемом примере легко выполняется аналитически, но для более сложного случая является трудоемкой и может вызвать возникновение значительного количества ошибок. Тогда приведение системы (6) к виду (7) удобно выполнить программно путем реализации (8), как сделано в настоящем примере (хотя здесь это и нерационально).
Начальные значения вектора переменных состояния системы (7) (начальные значения токов выпрямителя) задаются произвольно исходя из физического смысла. Так, для данного примера их можно принять нулевыми.
ЧЕТВЕРТЫЙ ЭТАП заключается в реализации функций системы управления выпрямителем. На рис.8 показаны зависимость Е2(t) и импульсы управления тиристорами VD1 u VD2 (зависимости Uу1(t) и Uу2(t) соответственно). Как следует из рисунка, все три зависимости являются периодическими функциями с периодом 2p радиан (360 электрических градусов), что при частоте питающей сети (частоте Е2) равной 50 Гц соответствует 0,02 сек. Кроме того, зависимости Uу1(t) и Uу2(t) "привязаны" к Е2(t) с помощью параметра a, называемого УГЛОМ УПРАВЛЕНИЯ. Угол управления отсчитывается от точки есРис. 8. Схема функционирования системы управления выпрямителем.
тественной коммутации тиристоров. Также из графиков следует, что импульсы управления на тиристоры VD1 и VD2 сдвинуты друг относительно друг на угол, равный p радиан или 180 электрических градусов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.