Вывод: Как видно из таблицы 5 при когерентном приеме вероятность ошибки первого рода и второго значительно меньше, чем при не когерентном приеме. Скорость передачи информации при когерентном приеме больше чем при не когерентном. Следовательно, выгодней использовать когерентный прием. Однако на практике, когерентный прием не реализуем из-за неидеальности приемников, источников и линий связи.
1.2.4 Расчет согласованного фильтра.
В идеале согласованный фильтр - это такое устройство, которое реагирует ( пропускает, вырабатывает определенный сигнал на выходе, короче, как-то отзывается.) только на тот сигнал, с которым он согласован. Имеется очень важное свойство согласованных фильтров. А именно, фильтр может отзываться не только на весь сигнал, но и на его часть (правда, реакция фильтра менее выражена).
В корреляционном приемнике корреляционный интеграл который используется для принятия решения решающим устройством формируется при помощи перемножителей и интеграторов. Если в системе передачи используется много сигналов,то нужно большое число корреляторов и интеграторов. Поэтому выгодней заменить корреляционную обработку фильтровой, т.е. вычислять корреляционный интеграл при помощи ЛИС-цепи.
Интеграл Дюамеля свидетельствует о том, что выходной сигнал ЛИС цепи представляет собой свертку двух функций – входного сигнала и импульсной характеристикой цепи :
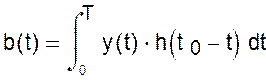
Считая сигнал известным получить корреляционный интеграл на выходе согласованного фильтра можем взяв следующее соотношение:
откуда получаем:
АЧХ согласованного фильтра имеет
такой же вид как модуль спектральной плотности сигнала 
.
Согласованный фильтр усиливает сильные спектры сигналов и ослабевает слабые.
где ωф0(z) плотность вероятности ошибки первого рода с согласованным
фильтром.
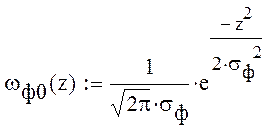
Так как вероятность появления нуля и единицы не равны то получаем следующее выражение:
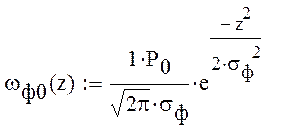
где σф равняется :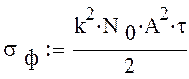 
Тогда получаем: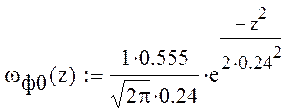 
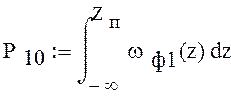где ωф1(z) плотность вероятности ошибки второго рода с согласованным
фильтром.
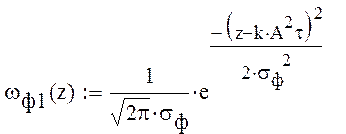
Так как вероятность появления нуля и единицы не равны то получаем следующее выражение:
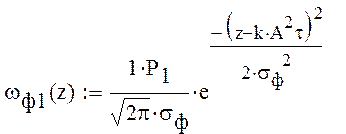
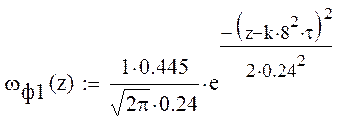
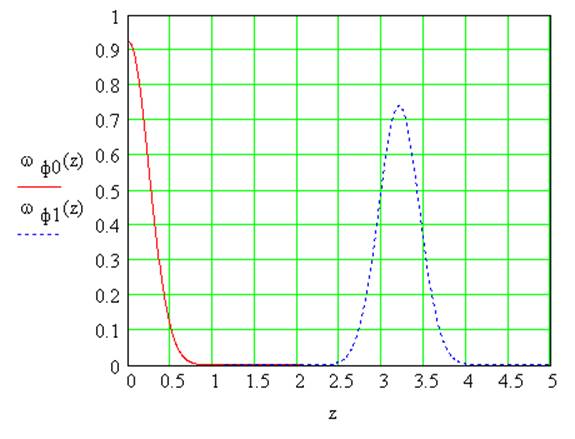
Рисунок 9: Построение ωф0(z) и ωф1(z).
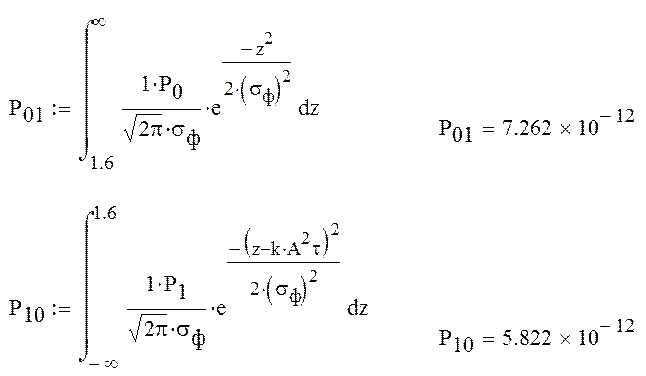
Найдем среднюю вероятность ошибки при когерентном приеме на выходе согласованного фильтра:
Определим отношение сигнала к помехе на входе фильтра:
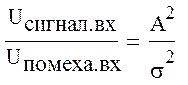
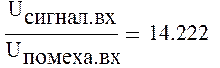
Определим отношение сигнала к помехе на выходе фильтра:
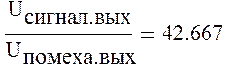
Определим в отношении сигнал к помехе за счет согласованной фильтрации:
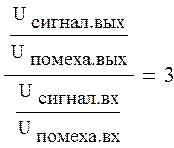
1.2.5 Канальное кодирование
Канальное кодирование повышает помехоустойчивость. С этой целью в систему связи вводят канальный кодер который и повышает помехоустойчивость путем увеличения избыточности то есть введением дополнительных контрольных символов. Реализовать такое кодирование можно с помощью кода Хемминга. Особенность кода Хемминга заключается в том , что путем введения дополнительных проверочных символов можно не только обнаружить ошибку но и исправить её. Но данный код не исправляет двукратные ошибки, а только обнаруживает их.
Закодируем фразу составленную в п 1.2.2 с помощью кода Хемминга.
Для этого разобьем нашу закодированную фразу по 4 символа:
умножим каждую комбинацию
на матрицу:
В результате чего выражение «держи вора крепко» в коде Хемминга принимает следующий вид:
«0001011010011111000101001110000000001110100111010010011101001111001110010011100101100100111111111101001111010011»
Рассчитаем вероятность однократной и двукратной ошибки:
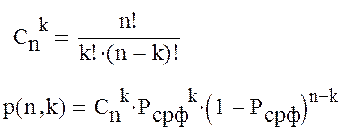
Вероятность однократной ошибки:
Вероятность двукратной ошибки :
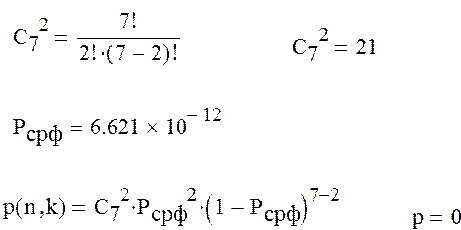
Приложение 1
Заключение.
В данной курсовой работе мы ознакомились и провели расчет системы связи. В процессе выполнения работы произведено кодирование дискретного сообщения с помощью кода Хаффмона, с помощью кода Хемминга ввели дополнительную избыточность для повышения помеха устойчивости, а также осуществлен прием сообщения.
Список литературы.
1. Теория электрической связи. Учебник для вузов / А.Г. Зюко, Д.Д. Кловский, М.В. Назаров, Л.М. Финк.—2-е изд., перераб. и доп.—М.: Радио и связь, 1986
2. Баскаков С.И. Радиотехнические цепи и сигналы: – М.: Высш. шк., 1988
3.
Полупроводниковая
схемотехника. У. Титце, К. Шенк – М.: «Мир», 1982
Оглавление
Введение
Задание и исходные данные
1.2.1 Обобщенная структурная схема
1.2.2 Кодирование источника
1.2.3. Расчет когерентного и не когерентного приема
1.2.4 Расчет согласованного фильтра
1.2.5 Канальное кодирование
Приложении 1
Заключение
Список литературы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.