Разработка системы связи для передачи дискретных сообщений. Согласованный фильтр для приема элементарной посылки, страница 2

Временные диаграммы

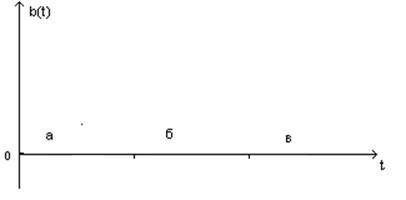
Рис2. Сигнал на выходе от источника.

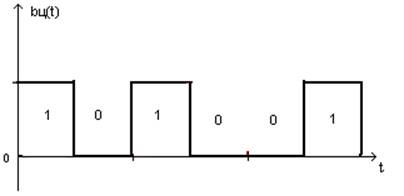
  Рис.3  Закодированный сигнал  на выходе кодера.

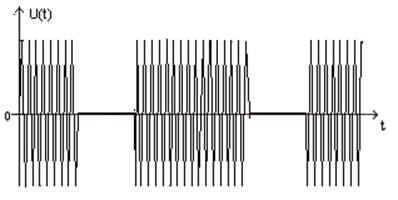
 Рис.4 Сигнал на выходе модулятора.

Рис.5 Сигнал в канале с шумом.

Рис.6 Сигнал на выходе демодулятора.

.

1.2.2 Кодирование источника.

Расположим алфавит в порядке убывания  вероятности.

bi	pi
б	0.11
к	0.11
п	0.098
н	0.097
с	0.096
д	0.089
р	0.078
и	0.077
м	0.064
о	0.06
в	0.049
ж	0.036
а	0.035
е	0.001

 

Таблица3

Произведем кодирование с помощью кода Хаффмона.

Схема кодирования приведена в приложении 1

После кодирования получаем следующие значения

bi	код	μ i
б	011	3
к	100	3
п	110	3
н	111	3
с	0000	4
д	0001	4
р	0010	4
и	0011	4
м	0101	4
о	1010	4
в	1011	4
ж	01000	5
а	010010	6
е	010011	6

Таблица 4

Так как появления символов не равновероятно, то для кодирования нужно использовать неравномерный код. Для таких кодов должно выполняться префиксное свойство.

Префиксное свой свойство – ни одна кодовая комбинация не является  началом другого.

Как видно из таблицы 4. префиксное свойство выполняется. Следовательно кодирование символов произведено правильно.

С  помощью полученных кодовых комбинаций закодируем фразу:

«Держи вора крепко»

«0001010011001001000001110111010001001001010000100100111101001010»

Энтропия- средние количество информации приходящиеся на один символ сообщений порождаемого данного источника.

Энтропия количества информации содержащееся в алфавите:

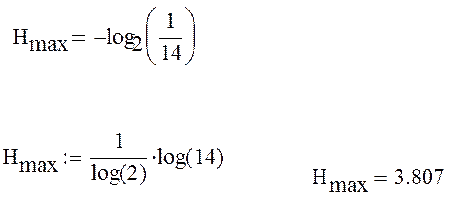
Энтропия алфавита:

 

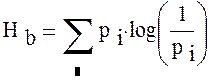
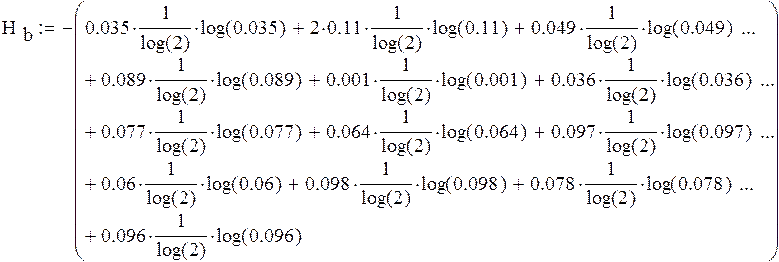
Избыточность:

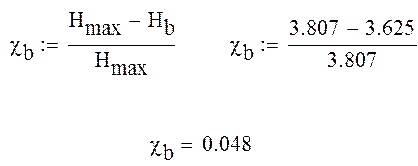
Среднее число двоичных символов:

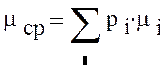
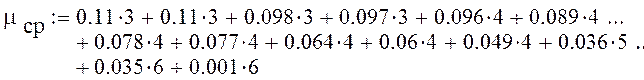
Вероятность появления 1 и 0.

а) Появления 1

   б) Появления 0

Скорость передачи информации без помех:

                  

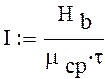
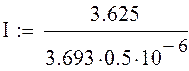
            1.2.3.  Расчет когерентного и не когерентного приема.

 

Ошибка 1-ого рода       «0» →  «1»  →      Р₀₁   Р₀

                                                                                                               Р_ср=Р₀Р₀₁+Р₁Р₁₀

Ошибка 2- ого рода      «1»→  «0»  →      Р₁₀   Р₁

где Р₀     -  Вероятность появления 0.

       Р₁    -  Вероятность появления 1.

       Р₀₁   -  Вероятность  ошибки первого рода.

       Р₁₀   -   Вероятность ошибки второго рода.

 гдеω₀(z) плотность вероятности ошибки первого рода:

Так как априорные вероятности не равны то помножаем ω₀(z) на P₀.

      где  ω₁(z)  плотность вероятности ошибки второго рода.

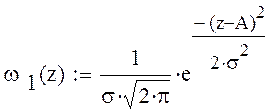
Так же помножаем ω₁(z) на P₁.

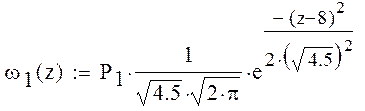
Построим графики зависимостиω₀(z)  и   ω₁(z)  и найдем точку пересечения которая и будет являться  идеальным порогом критерия идеального наблюдателя  Z_п.

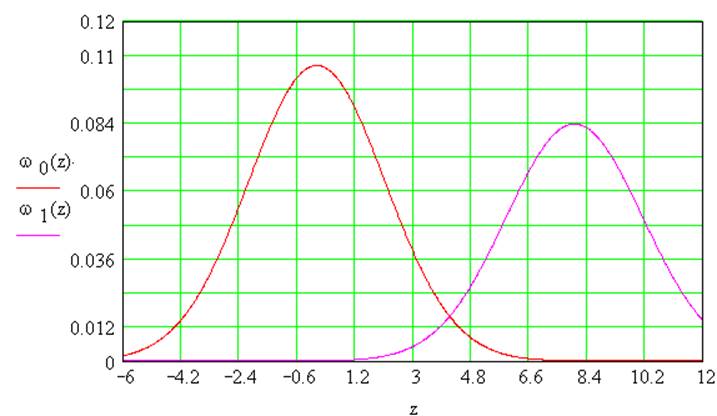
                  Рисунок 7: Графики ω₀(z)  и   ω₁(z) при когерентном приеме.

            

            

                                    

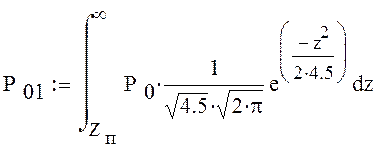
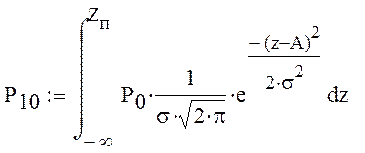
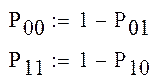
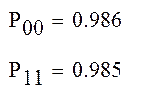
Найдем скорость передачи информации с шумом при когерентном приеме:

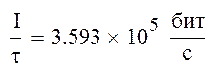
Некогерентный прием.

  где  ω_0н(z) плотность вероятности ошибки первого рода при некогерентном приеме.

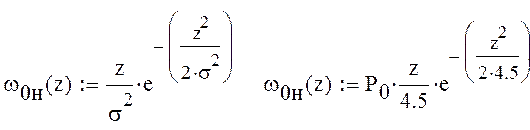
 где ω_1н(z)  плотность вероятности ошибки второго рода при некогерентном приеме.

       

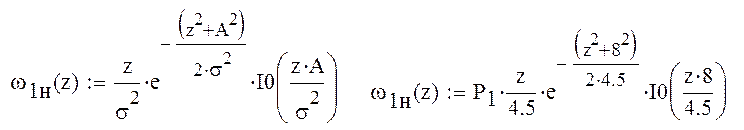
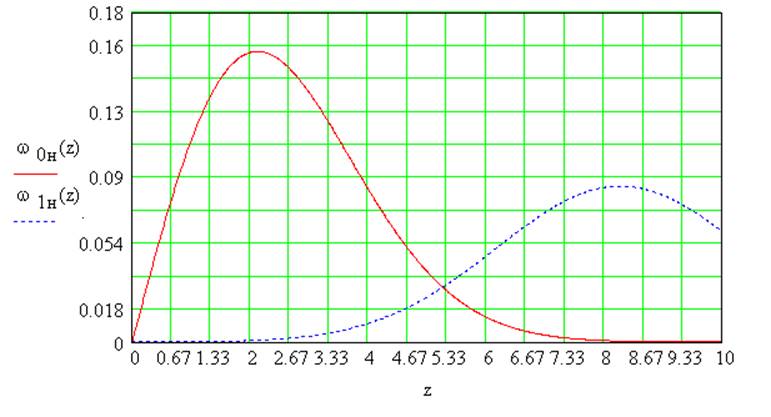
Рисунок 8: Графики ω₀(z)  и   ω₁(z) при  не когерентном приеме.

                 

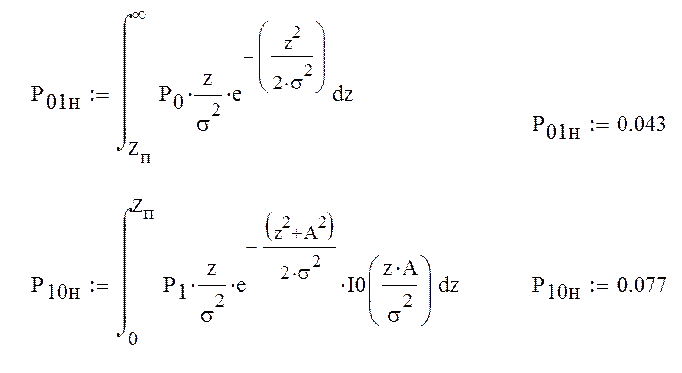
Найдем скорость передачи информации с шумом при некогерентном приеме:

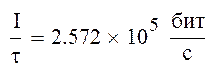
	Р01	Р10	Рср	I/τ (бит/с)
Когерентный прием	0,014	0,015	0,015
Некогерентный прием	0,043	0,077	0,058

Таблица 5: Данные расчетов при когерентном инее                    

                                                      когерентном приеме сигнала.