Случайные процессы и их воздействие на ЛИС-цепи. Исходный сигнал, записанный как линейная комбинация функций включения

1. Случайные процессы и их воздействие на ЛИС-цепи

1.1.  На вход заданной ЛИС-цепи воздействуют заданный сигнал и стационарный аддитивный белый шум с нулевым математическим ожиданием и спектральной плотностью мощности  (Вт/Гц), определяемой номером подварианта (табл. 3).

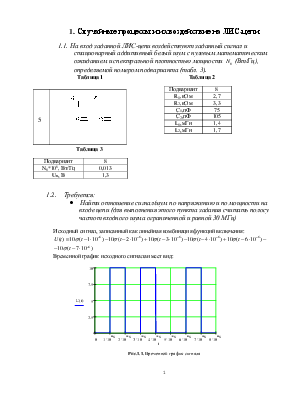
Таблица 1                                                            Таблица 2

                Таблица 3

1.2.  Требуется:

·   Найти отношение сигнал/шум по напряжению и по мощности на входе цепи (для выполнения этого пункта задания считать полосу частот входного шума ограниченной и равной 30 МГц)

Исходный сигнал, записанный как линейная комбинация функций включения:

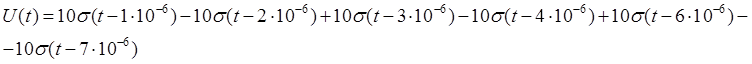
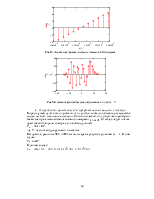
Временной график исходного сигнала имеет вид:

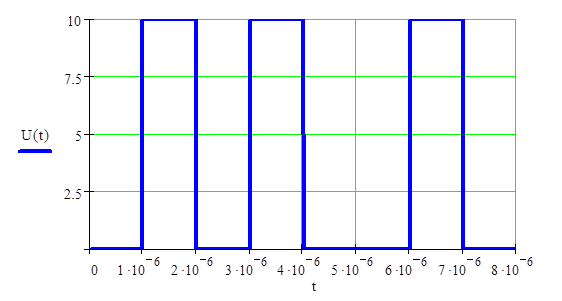
Рис.1.1. Временной график сигнала

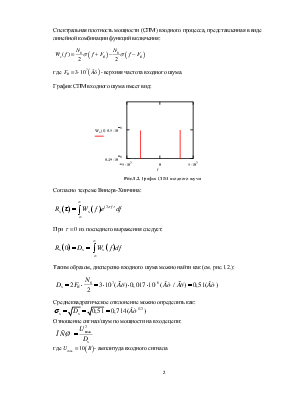
Спектральная плотность мощности (СПМ) входного процесса, представленная в виде линейной комбинации функций включения:

где - верхняя частота входного шума.

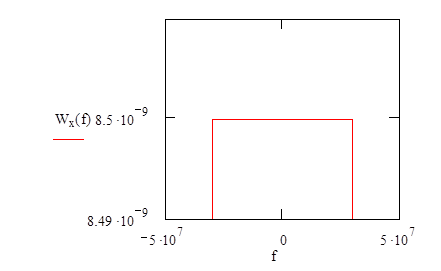График СПМ входного шума имеет вид:

Рис.1.2. График СПМ входного шума

Согласно теореме Винера-Хинчина: 

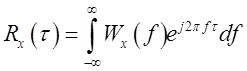
При  из последнего выражения следует:

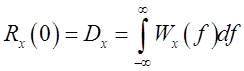
Таким образом, дисперсию входного шума можно найти как (см. рис.1.2.):

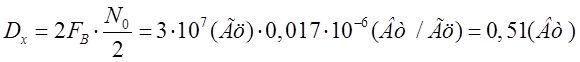
Среднеквадратическое отклонение можно определить как:

Отношение сигнал/шум по мощности на входе цепи:

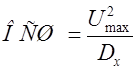
где - амплитуда входного сигнала

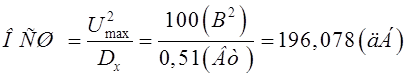
Отношение сигнал/шум по напряжению на входе цепи:

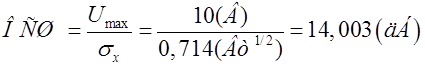
·   Найти СПМ шума и ОСШ по напряжению и по мощности на выходе цепи.

В РГЗ №1 было определено, что КЧХ заданной ЛИС-цепи имеет вид:

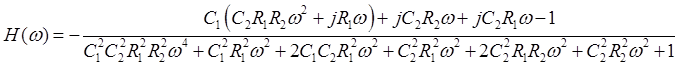
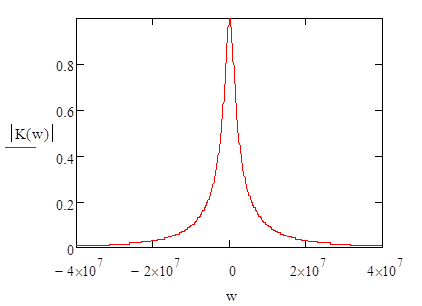
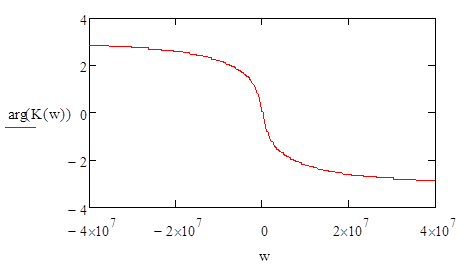График модуля и аргумента данной функции представлен ниже:

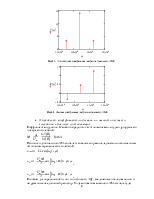
                                    Рис.1.3. Графики АЧХ и ФЧХ заданной ЛИС-цепи

Отклик ЛИС-цепи на стационарный случайный процесс имеет спектральную плотность мощности, равную входной СПМ, умноженной на квадрат модуля КЧХ (т.е. на квадрат АЧХ цепи):   

Это выражение описывает спектральный метод анализа ЛИС-цепей при случайных стационарных воздействиях.

СПМ входного воздействия (белого шума) равна:

Таким образом, СПМ шума на выходе:

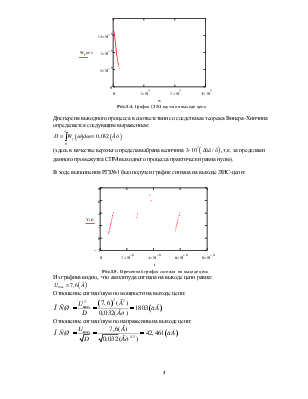
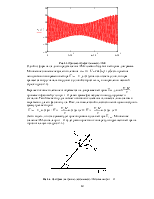
График СПМ шума на выходе имеет вид:

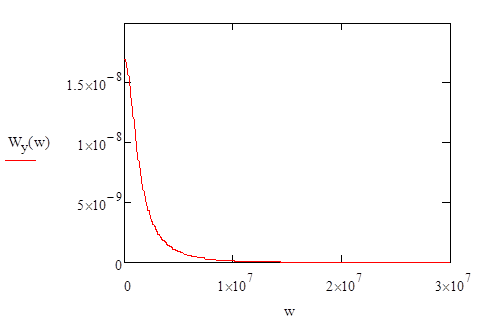
                                                      Рис.1.4. График СПМ шума на выходе цепи

Дисперсия выходного процесса в соответствии со следствием теорема Винера-Хинчина определяется следующим выражением:

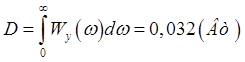
(здесь в качестве верхнего предела выбрана величина , т.к. за пределами данного промежутка СПМ выходного процесса практически равна нулю).

В ходе выполнения РГЗ№1 был получен график сигнала на выходе ЛИС-цепи:

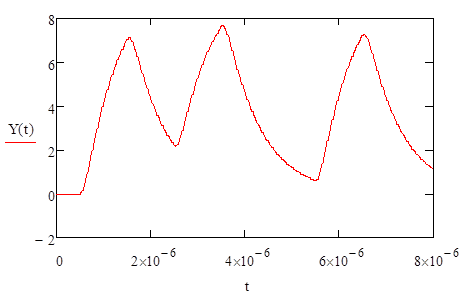
                                         Рис.1.5.  Временнойграфик сигнала  на выходе цепи

Из графика видно,  что амплитуда сигнала на выходе цепи равна:

Отношение сигнал/шум по мощности на выходе цепи:

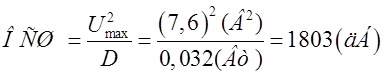
Отношение сигнал/шум по напряжению на выходе цепи:

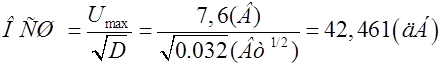
·  Найти эффективную ширину спектра и интервал корреляции шума на выходе цепи

Пусть исследуемый случайный процесс характеризуется функцией - односторонним спектром мощности, причем - экстремальное значение этой функции. Заменим мысленно данный случайный процесс другим процессом, у которого СПМ постоянна и равна   в пределах эффективной полосы частот , выбираемой из условия равенства мощностей обоих процессов:

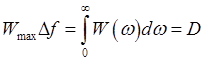
Отсюда получается формула для эффективной ширины спектра:

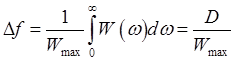
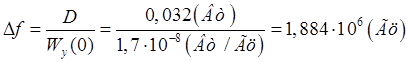
Случайные процессы, изучаемые статистической радиотехникой, как правило, обладают следующим свойством: их функция корреляции стремиться к нулю с увеличением временного сдвига . Чем быстрее убывает функция , тем меньшей оказывается статистическая связь между мгновенными значениями случайного сигнала в два несовпадающих момента времени.

Числовой характеристикой, служащей для оценки "скорости изменения" реализаций случайного процесса, является интервал корреляции .

Интервал корреляции – величина, обратная эффективной ширине спектра, поэтому:

Если известна информация о поведении какой-либо реализации "в прошлом", то возможен вероятностный прогноз случайного процесса на время порядка . Однако, попытка прогнозирования на время, существенно превышающее интервал корреляции, окажется безрезультативной – мгновенные значения, столь далеко отстоящие во времени практически некоррелированы, т.е. среднее значение произведения  стремится к нулю. 

·   Построить графики плотности распределения вероятности мгновенного значения шума и смеси сигнала с шумом на выходе цепи для момента времени, когда сигнал максимален

Мгновенное значение шума на выходе  цепи распределено по нормальному закону с нулевым математическим ожиданием и дисперсией  .

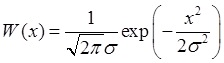
Мгновенное значение смеси сигнала с шумом на выходе цепи также распределено по нормальному закону, но математическое ожидание равно (т.к. выбран момент времени, когда сигнал максимален).

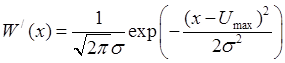
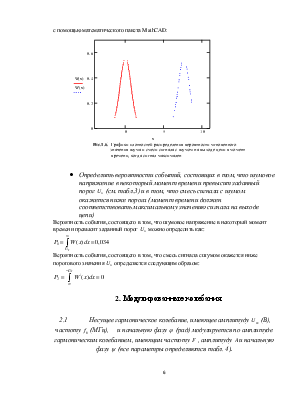
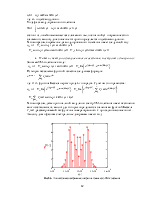
Ниже приведены графики функций плотностей распределения вероятности, построенные с помощью математического пакета MathCAD:

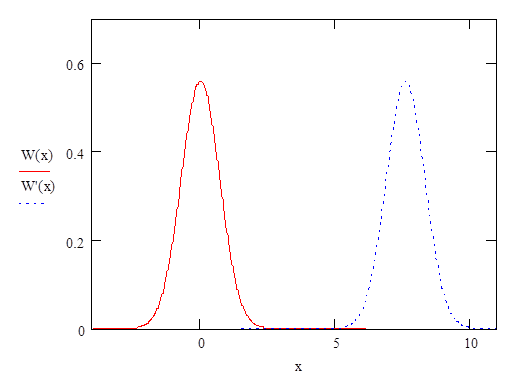
                                 Рис.1.6.  Графики плотностей распределения вероятности мгновенного значения шума и смеси сигнала с шумом на выходе цепи в момент