Гармонические колебания. Основные понятия и определения. Способы представления гармонических колебаний

Лекция № 5

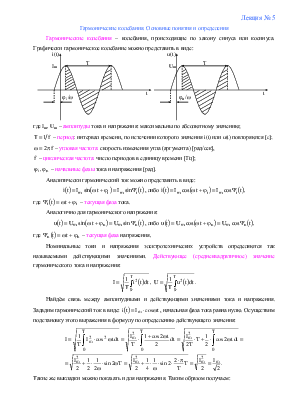
Гармонические колебания. Основные понятия и определения

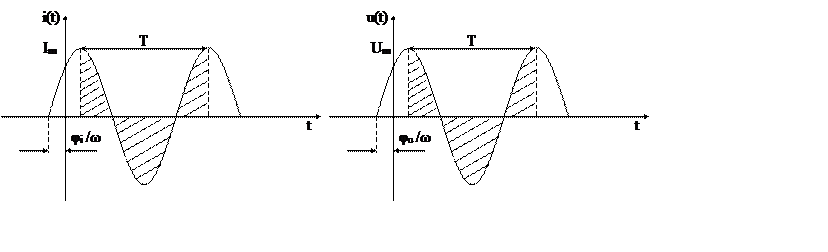Гармонические колебания – колебания, происходящие по закону синуса или косинуса. Графически гармоническое колебание можно представить в виде:

где I_m, U_m – амплитуды тока и напряжения: максимальны по абсолютному значению;

 – период: интервал времени, по истечении которого значения i(t) или u(t) повторяются [c];

– угловая частота: скорость изменения угла (аргумента) [рад/сек],

 – циклическая частота: число периодов в единицу времени [Гц];

, – начальные фазы тока и напряжения [рад].

Аналитически гармонический ток можно представить в виде:

, либо , где  – текущая фаза тока.

Аналогично для гармонического напряжения:

, либо , где  – текущая фаза напряжения,

Номинальные токи и напряжения электротехнических устройств определяются так называемыми действующими значениями. Действующее (среднеквадратичное) значение гармонического тока и напряжения:

, .

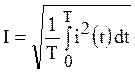Найдём связь между амплитудными и действующими значениями тока и напряжения. Зададим гармонический ток в виде: , начальная фаза тока равна нулю. Осуществим подстановку этого выражения в формулу по определению действующего значения:

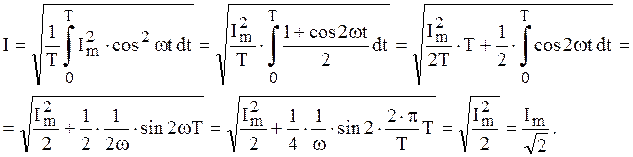
Такие же выкладки можно показать и для напряжения. Таким образом получаем:

,  – связь между амплитудными и действующими значениями тока и напряжения.

Среднее значение гармонического тока и напряжения равно нулю. Это можно доказать, если воспользоваться формулами по определению среднего значения периодического негармонического тока и напряжения:

, .

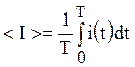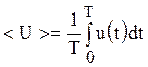Способы представления гармонических колебаний

Гармонические колебания представляют в виде:

1.  временных диаграмм;

2.  векторных диаграмм;

3.  комплексных чисел;

4.  амплитудных и фазовых спектров;

Временное представление (ранее было показано) наглядно, но затруднительно при решении задач, поскольку требует проведения громоздких тригонометрических преобразований.

Векторное представление является более удобным, при этом каждому колебанию ставится в соответствие вращающийся вектор определенной длины с заданной начальной фазой.

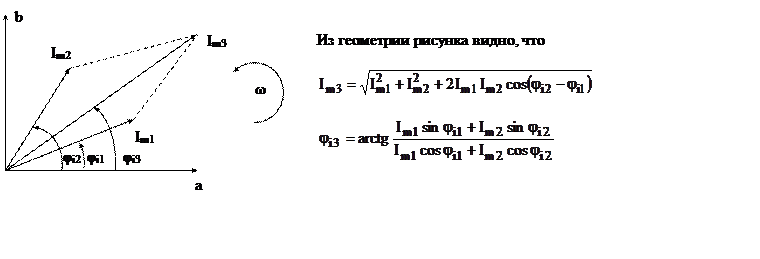Пример. Пусть имеем колебания токов:  и . Определим сумму этих токов: .

 – фазовый сдвиг между колебаниями токов i₁ и i₂.

Векторной диаграммой называют совокупность векторов, изображающих гармонические колебания в электрической цепи. Векторные диаграммы строят для амплитудных или действующих значений.

Представления гармонических колебаний с помощью комплексных чисел лежат в основе символического метода расчета электрических цепей (метод комплексных амплитуд).

 →  – комплексная амплитуда, где (мнимая единица).

 →  – комплекс действующего значения, причем .

,  – запись в показательной форме. Существует запись в алгебраической форме, для этого используем формулу Эйлера: .

, где ,

Пример. Решим предыдущую задачу с помощью символического метода:

Каждому гармоническому колебанию тока ставим в соответствие комплекс тока:

   ,

   .

Следует заметить, что комплекс тока мы представили как в показательной, так и в алгебраической форме. Из теории комплексных чисел известно, что если совершается операция сложения (вычитания) комплексное число удобно представлять в алгебраической форме, если совершается операция умножения (деления) комплексное число удобно представлять в показательной форме. В данном примере осуществляется операция сложения двух гармонических колебаний, поэтому комплексы токов удобно представить в алгебраической форме:

Определяем суммарный ток: .

Последнее выражение представлено в алгебраической форме, его необходимо перевести в показательную. Используем соотношение, которое позволяет комплексное число перевести из алгебраической формы в показательную форму:

, где  – модуль комплексного числа,  – аргумент комплексного числа.

Таким образом, суммарный ток в показательной форме можно записать