Силовой расчет рычажного механизм. Построение плана ускорений механизма. Нормальное ускорение в относительном движении

2  СИЛОВОЙ  РАСЧЕТ  РЫЧАЖНОГО  МЕХАНИЗМА

Для  положения  механизма  при  φ₁ = 60⁰  строим  план  положения  в  масштабе     и  план  скоростей  в  масштабе  .

2.1  Построение  плана  ускорений  механизма

Так  как  частота  вращения  ведущего  звена  постоянна,  то  точка  А  имеет  только  нормальное  ускорение 

                                                  (2.1)                                              

Выбираем  масштабный  коэффициент   

Из  произвольной  точки  p_a  строим  вектор  p_aa   этот  вектор  направлен  к  центру  вращения,  от  точки А  к  точке  О  параллельно  звену  АО.

Ускорение  точки  С  определяется  системой и  двух  векторных  уравнений

                                                           (2.2)  

где    - нормальное  ускорение  в  относительном  движении,  направленное  от точки  С  к  А  вдоль  звена  СА,  м/с²,

                                                                                                 (2.3)

 - касательное  ускорение   в  относительном  движении,  направленное    перпендикулярно  звену   СА,  м/с²;

 - нормальное  ускорение  в  движении,  направленное  от  точки  С  к  О₂  вдоль  звена  СО₂,  м/с²,            

                                   (2.4)

 - касательное  ускорение   в  движении,  направленное  перпендикулярно звену   СО₂,  м/с².

Для  определения  положения  точки  С  на  плане  ускорений  из  точки  плана  a  строим   вектор  an2,  соответствующий  ускорению  

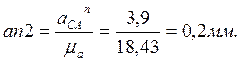
Через  конец  вектора  an2  проводим  прямую  в  направлении  вектора  ,  перпендикулярно  звену  СА.  Далее  через  полюс  плана  p_a  строим   вектор  p_an3,  соответствующий  ускорению  

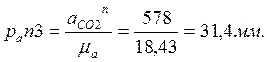
Через  конец  вектора  p_an3  проводим  прямую  в  направлении  вектора  ,  перпендикулярно  звену  СО₂.  Точка  пересечения  последних  двух  линий  изображает  конец  вектора  ускорения  точки  С.

Положение  точки  В  на  плане  ускорений  определим  методом  подобия:

;

мм.

Зная  положение  точки  b  соединяем  эту  точку  с  полюсом  ускорений  и  получим:

 мм.

Положение  точки  D  на  плане  ускорений  определим  методом  подобия:

;

мм.

Положение  точки  D  определим  проведя  прямую из  точки  b  плана  через  полюс    плана  ускорений  прямую  на  расстояние  330  мм.

Ускорения  точек     определяются методом  подобия.

Численные  величины  ускорений  определим  по  формулам

        

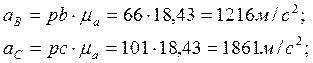
2.2  Определение  инерционных  нагрузок  звеньев

Силы  инерции  звеньев  определяем  по  формуле

                                               (2.5)

где  m – масса  звена,  кг;

a_S – ускорение  центра  тяжести  звена,  м/с².

Знак  минус  показывает,  что  вектор  F_И  направлен  противоположно  вектору  a_S.

Определим  силы  инерции:

сила  инерции  звена  2

         Н;

сила  инерции  звена  3

Н.

Звено  3  совершает  вращательное  движение.  Поэтому   F_И3   не  будет  проходить  через  S₃,  а  проходит  через  точку  качания  К₃ и будет  направлена   в  сторону  противоположно  вектору  .  Положение  точки  качания  К₃  определим  по  формуле

;                                          (2.6)

                                           (2.7)                                                        

Так  как  ,  то 

Аналогично  определяем  для  звена  2,   ,  тогда  получаем,  что  сила  инерции  звена  3  прикладывается  в  точке  S₃  и  направлена   в  сторону  противоположно  вектору  .  Сила  инерции  звена  2  прикладывается  в  точке  S₂  и  направлена   в  сторону  противоположно  вектору  .

2.3  Определение  реакций   в  кинематических  парах  и  уравновешивающей  силы

Определение  реакций  в  кинематических  парах  начинаем  с  группы  звеньев,  наиболее  удаленной  от  ведущего  звена  АО,  с  группы  Ассура  со  звеньями  4  и  5.

Вычерчиваем  группу  4,5  в  масштабе    и  в  соответствующих  точках  звеньев  прикладываем  все  действующие  силы.  Отброшенные  связи  заменяем  реакциями    и  .  Силу    разложим  на  составляющие   и    так  как  направление  этой  силы  неизвестно. 

Запишем  векторное  уравнение  равновесия 

                             (2.8)

В  этом   уравнении  неизвестны   силы  ,   и  .  Величину  можно  определить  из  уравнения  моментов  сил  звена  4  относительно  точки  О:

                                                                                  (2.9)

Величину  можно  определить  из  уравнения  моментов  сил   относительно  точки  А:

 R₀₅ · 28= 0;                                                                                    (2.10)

Так  как  на  группу  5-4  не  действуют  силы  не  равные  нулю,  то  план  сил  не  строим.

Выполним  силовой  расчет  группы  Ассура  со  звеньями  2   и  3.

Вычерчиваем  группу  2,3  в  масштабе    и  в  соответствующих  точках  звеньев  прикладываем  все  действующие  силы.  Отброшенные  связи  заменяем  реакциями   и  .  Силы  ,   разложим  на  составляющие  , ,  и  , так  как  направления  ,   неизвестно.

Запишем  векторное  уравнение  равновесия 

                     (2.11)

В  этом   уравнении  неизвестны   силы  , ,  и  .  Величину    можно  определить  из  уравнения  моментов  всех  сил  относительно  точки  С

                                                 (2.12)    

Величину    можно  определить  из  уравнения  моментов  всех  сил  относительно  точки  А

                                               (2.13)                                                      

Строим   план  сил  в  масштабе    в  соответствии  с  уравнением  (2.11)  и  из  него  определяем 

Силовой  расчет  ведущего  звена  АО.

Вычерчиваем  ведущее  звено  в  масштабе    и  в  соответствующих  точках  прикладываем  все  действующие  силы.  Уравновешивающую  силу     прикладываем  в  точке  А  перпендикулярно  звену  АО.

Составим   векторное  уравнение  равновесия 

                                                   (2.14)

Величину  уравновешивающей  силы  определим  из  уравнения  моментов  всех  сил  относительно  точки  О:

                                                                          (2.15)

В  масштабе    строим  план  сил,  из  которого  определяем  реакцию  в  шарнире  О:

Определяем  уравновешивающий  момент  на  звене  АO:

.

2.4  Определение  уравновешивающего  момента  по  методу  профессора 

Н.Е. Жуковского 

В  масштабе    строим  повернутый  на  90⁰  план  скоростей  и  в  соответствующих  точках  плана  прикладываем  все  внешние  силы  и  силы  инерции  звеньев.  Составляем  уравнение  моментов  всех  сил  относительно  полюса  повернутого  плана  скоростей,  беря  плечи  по  чертежу  в  мм: 

                                    (2.16)

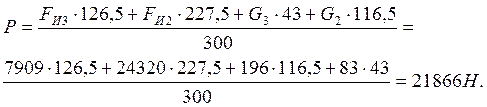
Определяем  уравновешивающий  момент  на  звене  АО:

.

Определяем  расхождение  результатов  определения  уравновешивающего  момента  методом  планов  сил  и  методом  профессора  Н.Е. Жуковского:

.