Привод к центральному валу ленточного конвейера. Кинематический расчет и выбор электродвигателя. Выбор материалов и определение допускаемых напряжений

ЗАДАНИЕ

Задание 10. Спроектировать привод к центральному валу ленточного конвейера по схеме

Мощность на валу N₄ = 3,8 кВт, угловая скорость вращения вала          об/мин.

СОДЕРЖАНИЕ

1 Кинематический расчет и выбор электродвигателя                               4

2 Выбор материалов и определение допускаемых напряжений               7

3 Расчет тихоходной  прямозубой ступени редуктора                              10

4 Расчет быстроходной косозубой ступени редуктора                             13

5 Расчет клиноременной передачи                                                             14

6 Расчет валов                                                                                              15

7 Подбор подшипников и выбор шпонок                                                   26

8 Выбор муфт                                                                                               28

9 Выбор смазки                                                                                            29

10 Выбор посадок деталей                                                                          30

11 Порядок сборки редуктора                                                                     31

Литература                                                                                                   32

1 Кинематический расчет и выбор электродвигателя

Рисунок 1 – Кинематическая схема редуктора

Определяем потребную мощность электродвигателя для всего привода.

Требуемая мощность электродвигателя определяется по формуле:

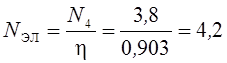 кВт, где  – общий КПД привода;

.

где  – КПД клиноременной передачи ();

– КПД зубчатой цилиндрической косозубой передачи в масляной ванне ();

 – КПД зубчатой цилиндрической прямозубой пары ().

По таблице П26 [4] выбираем трехфазный асинхронный короткозамкнутый электродвигатель серии 4A100L2У3:  кВт;                 об/мин.

Определяем общее передаточное число привода:

;

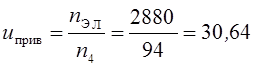По таблице 4.1 [1] принимаем передаточные отношения:  клиноременной передачи  Тогда

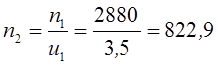об/мин;

;

;

.

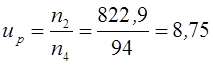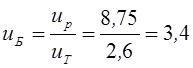Определяем частоты вращения валов привода:

 об/мин;

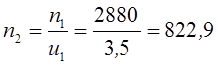 об/мин;

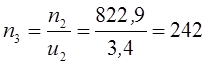 об/мин;

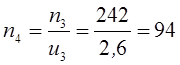 об/мин.

Определяем мощности на валах привода:

 кВт;

 кВт;

 кВт;

 кВт.

Определяем крутящие моменты на валах:

 ;

;

;

.

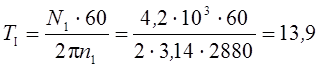
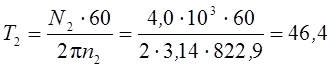
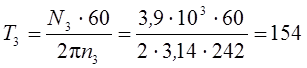
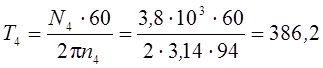
Определяем ориентировочно диаметры всех валов привода:

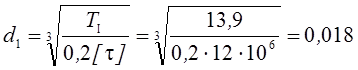м         или  мм;

м        или  мм;

м        или  мм;

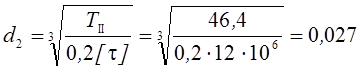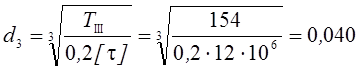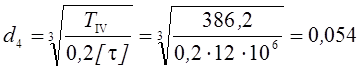м        или  мм.

2 Выбор материалов и определение допускаемых напряжений

Принимаем:

-  для колёс – НВ 230..260, σ_в = 850 МПа; σ_т = 550 МПа;

-  для шестерни второй ступени – НВ 260..280, σ_в = 950 МПа; σ_т = 700 МПа;

-  для шестерни первой ступени: HRC 50..59, σ_в = 1000 МПа; σ_т = 800 МПа.

Срок службы привода равен 4000 часов.

Допускаемые контактные напряжения.

Для колёс:МПа; МПа.

Для шестерни второй ступени: МПа; МПа;

Для шестерни первой ступени: МПа; МПа.

МПа.

Допускаемые напряжения изгиба

Для колёс:МПа; МПа.

Для шестерни второй ступени: МПа; МПа.

Для шестерни первой ступени: МПа; МПа.

МПа

3 Расчёт тихоходной прямозубой ступени редуктора

Предварительный расчёт межосевого расстояния выполняем по формуле:

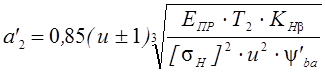
По рекомендации принимаем .

По графику .

Определим :

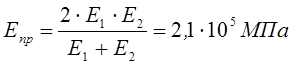, где  - приведенный модуль упругости;

,-модули упругости.

Подставив в формулу для межосевого расстояния и округлив до значения стандартного ряда получаем  мм.

Находим ширину колеса

мм.

По таблице принимаем . Находим модуль

мм.

Назначаем m = 2,5 мм.

Определим суммарное число зубьев:

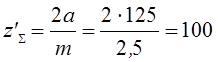
Определим число зубьев шестерни:

Принимаем .

Число зубьев колеса: .

Фактическое передаточное число:

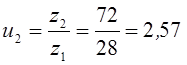
Делительные диаметры шестерни и колеса:

мм;

мм.

Диаметры вершин зубьев шестерни и колеса:

мм;

мм.

Выполняем проверочный расчёт на усталость по контактным напряжениям по формуле:

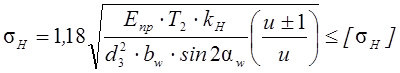
где ;

 .

Подставив полученные значения, получим:

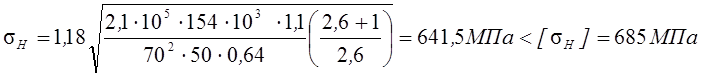
D = 6,35 % > [D] = 4 %,

Поэтому

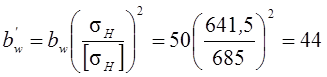мм.

мм.

В соответствии с рядом стандартных модулей оставляем модуль, равный 2,5 мм.

Окончательно d₁ = 70 мм, d₂ = 180 мм, b_w = 44 мм.

Выполняем проверочный расчёт по напряжениям изгиба:

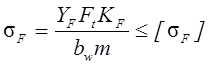
По графику  при х = 0:

-  для шестерни: ;

-  для колеса: .

Расчёт выполняем по тому из колёс пары, у которого меньше отношение .

-  для шестерни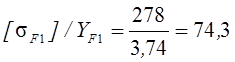

-  для колеса .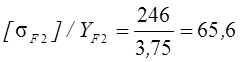

Расчёт ведём по колесу.

По графику . При этом .

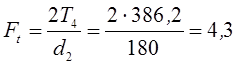Далее кН.

Подставив полученные значения в исходную формулу, получим:

.

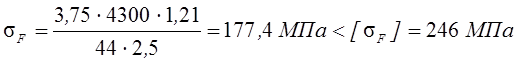Выполняем проверочный расчёт на заданную перегрузку:

.

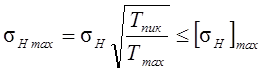
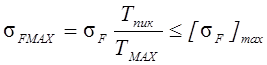
Условия прочности соблюдаются.

4 Расчёт быстроходной косозубой ступени редуктора

Предварительный расчёт межосевого расстояния выполняем по формуле:

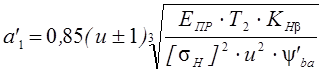
По рекомендации принимаем .

По графику .

Определим :

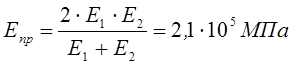, где  - приведенный модуль упругости;

,-модули упругости.

Подставив в формулу для межосевого расстояния и округлив до значения стандартного ряда получаем  мм.

Находим ширину колеса

мм.

По таблице принимаем . Находим модуль

мм.

Назначаем m = 2 мм.

Определим суммарное число зубьев:

Определим число зубьев шестерни:

Принимаем .

Число зубьев колеса: .

Фактическое передаточное число:

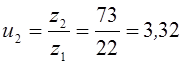
Делительные диаметры шестерни и колеса:

мм;

мм.

Диаметры вершин зубьев шестерни и колеса:

мм;

мм.

Выполняем проверочный расчёт на усталость по контактным напряжениям по формуле:

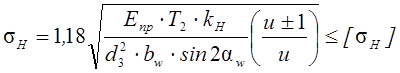
где ;

 .

Подставив полученные значения, получим:

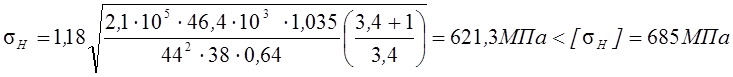
D = 9,3 % > [D] = 4 %,

Поэтому

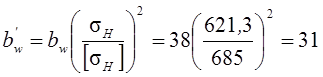мм.

мм.

В соответствии с рядом стандартных модулей принимаем модуль, равный 1,5 мм.

Окончательно d₁ = 43,5 мм, d₂ = 147 мм, b_w = 31 мм.

Выполняем проверочный расчёт по напряжениям изгиба:

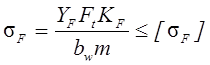
По графику  при х = 0:

-  для шестерни: ;

-  для колеса: .

Расчёт выполняем по тому из колёс пары, у которого меньше отношение .

-  для шестерни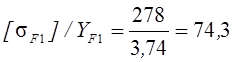

-  для колеса .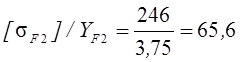

Расчёт ведём по колесу.

По графику . При этом .

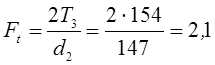Далее кН.

Подставив полученные значения в исходную формулу, получим:

.

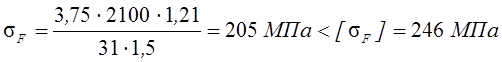Выполняем проверочный расчёт на заданную перегрузку:

.

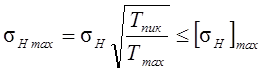
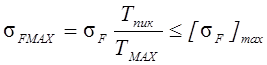
Условия прочности соблюдаются.

5 Расчет клиноременной передачи

Определяем диаметр малого шкива

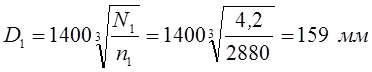
По ГОСТ 17383-73 выбираем размер малого шкива D₁=160мм.

Определяем диаметр большого шкива

По ГОСТу диаметр шкива: D₂=560мм.

Определяем межосевое расстояние а и длину ремня l.

Предварительно назначаем а^’=560 мм.

Принимаем l_p = 2500 мм, h = 8 мм, b₀ = 13 мм, b_p = 11 мм, A = 81 10^-6 м²,      q = 0,1 кг/м.

Определим межосевое расстояние

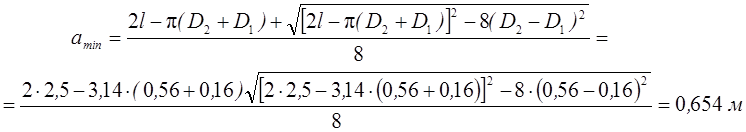
Проверяем найденное значение по рекомендации

Определяем угол обхвата α

Мощность, передаваемая одним ремнём

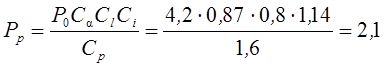 кВт.

Число ремней

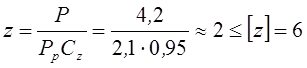
Окружная скорость передачи

Эта скорость находится в пределах, рекомендуемых для среднескоростных передач (v≤ 25м/с).

Сила предварительного натяжения одного ремня

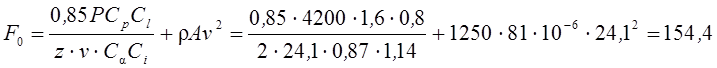 Н.

Равнодействующая нагрузка на вал

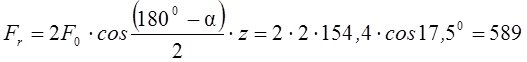Н

Ресурс наработки

ч.

6 Расчет валов

Выполняем проектный расчет валов и их опор двухступенчатого цилиндрического редуктора с косозубой быстроходной ступенью. Материал валов – сталь 45, улучшенная, Срок службы – 4000 ч, нагрузка переменная.

Вал 1: Н×м;  об/мин; мм;

Вал 2: Н×м;  об/мин; мм; мм;

Вал 3: Н×м;  об/мин; мм;

( - диаметры шестерен, - диаметры колес).

Определяем силы, действующие в зацеплении редуктора с прямозубой и косозубой ступенями (рисунок 1).

Рисунок 1 – Схема нагружения валов редуктора и силы, действующие в косозубом и прямозубом цилиндрических зацеплениях

Косозубая пара:

Прямозубая пара:

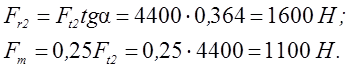
Рассчитываем ведущий вал (рисунок 2)

Строим расчётную схему сил, действующих на вал 1 в вертикальной и горизонтальной плоскостях, .

Рисунок 2 – Расчетная схема сил, действующих на вал 1 в вертикальной и горизонтальной плоскостях а) опорные реакции в вертикальной плоскости

,

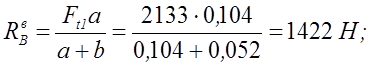
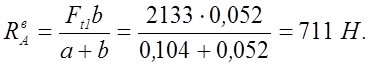
Проверка:

б) опорные реакции в горизонтальной плоскости

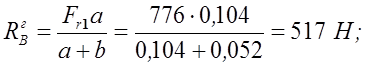
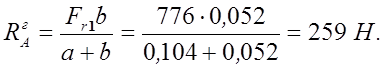
Проверка:

Изгибающие моменты в вертикальной и горизонтальной плоскостях

Для получения общей эпюры изгибающих моментов суммируем две полученные эпюры

Для подбора подшипников качения определяем суммарные опорные реакции